- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Золотое сечение в архитектуре, музыке и искусстве
Содержание
- 2. Золотое сечение (золотая пропорция, деление в крайнем и среднем
- 3. Число называется также золотым
- 4. История золотого сеченияПринято считать, что понятие о
- 5. Французский архитектор Ле Корбюзье нашел, что в
- 6. ПифагорКвадрат Пифагора и диагональ этого квадрата были
- 7. ЕвклидВ дошедшей до нас античной литературе золотое
- 8. Одним из красивейших произведений древнегреческой архитектуры является
- 9. Храм Василия Блаженного Трудно найти человека, который
- 10. Известный русский архитектор М. Казаков в своем
- 11. Золотое сечение в пятиконечной звездеПостроение золотого сечения
- 12. Ряд Фибоначчи
- 13. В 1202 г вышел в свет его
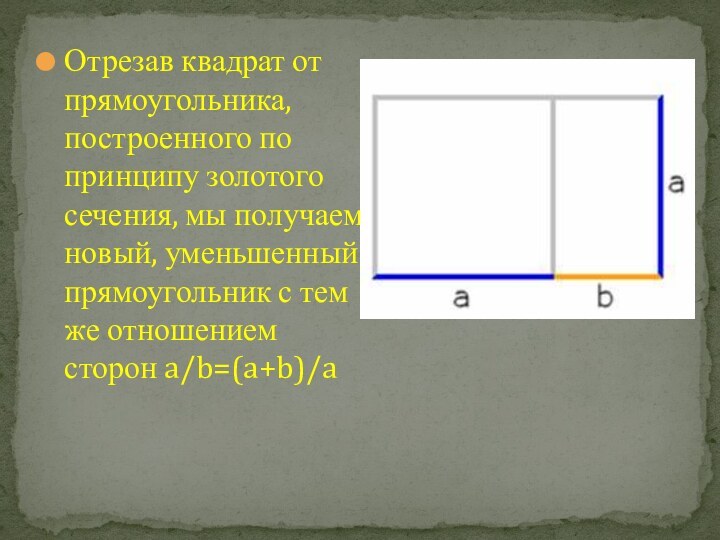
- 14. Отрезав квадрат от прямоугольника, построенного по принципу
- 16. Золотое сечение в картине
- 17. Скачать презентацию
- 18. Похожие презентации
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении)Золотое сечение — соотношение двух величин, равное соотношению их суммы к большей из данных величин. Приблизительная величина золотого сечения равна 1,6180339887. В процентном округлённом значении — это деление величины















Слайд 3
Число называется также золотым числом.
С
математической точки зрения, отношение большей части к меньшей в
золотом сечении выражается квадратичной иррациональностьюи, наоборот, отношение меньшей части к большей
Слайд 4
История золотого сечения
Принято считать, что понятие о золотом
делении ввел в научный обиход Пифагор, древнегреческий философ и
математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их созданииСлайд 5 Французский архитектор Ле Корбюзье нашел, что в рельефе
из храма фараона Сети I в Абидосе и в
рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления
Слайд 6
Пифагор
Квадрат Пифагора и диагональ этого квадрата были основанием
для построения динамических прямоугольников . Платон (427...347 гг. до
н.э.) также знал о золотом делении.Платон
Слайд 7
Евклид
В дошедшей до нас античной литературе золотое деление
впервые упоминается в “Началах” Евклида. Во 2-й книге “Начал”
(ок. 300 лет до н. э.) дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), и др.Слайд 8 Одним из красивейших произведений древнегреческой архитектуры является Парфенон
(V в. до н. э.).
Парфенон имеет 8 колонн по
коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.
Слайд 9
Храм Василия Блаженного
Трудно найти человека, который бы
не знал и не видел собора Василия Блаженного на
Красной площади. Храм этот особенный; он отличается удивительным разнообразием форм и деталей, красочных покрытий; ему нет равных в нашей стране. Архитектурное убранство всего собора продиктовано определенной логикой и последовательностью развития форм. Исследуя его, пришли к выводу о преобладании в нем ряда золотого сечения. Если принять высоту собора за единицу, то основные пропорции, определяющие членение целого на части, образуют ряд золотого сечения: 1 : j : j 2 : j 3 : j 4 : j 5 : j 6 : j 7, где j =0,618Слайд 10 Известный русский архитектор М. Казаков в своем творчестве
широко использовал “золотое сечение”.
Его талант был многогранным. Например, “золотое
сечение” можно обнаружить в архитектуре здания сената в Кремле.По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется больницей имени Н.И. Пирогова
Слайд 13 В 1202 г вышел в свет его математический
труд “Книга об абаке” (счетной доске), в котором были
собраны все известные на то время задачи. Одна из задач гласила “Сколько пар кроликов в один год от одной пары родится”. Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, и т.д.
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи).