- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Порядок и хаос
Содержание
- 2. Все мои произведения — это игры. Серьезные
- 3. М.К. Эшер
- 4. «Порядок и хаос»Звездный додекаэдр (двенадцатигранник) , расположенный
- 5. М. Эшер о себе:«Я так ни разу
- 6. Многогранники Правильные геометрические тела - многогранники
- 7. О картине:Большое количество различных многогранников может быть
- 8. О других работах с многогранникамиФигуры, полученные объединением
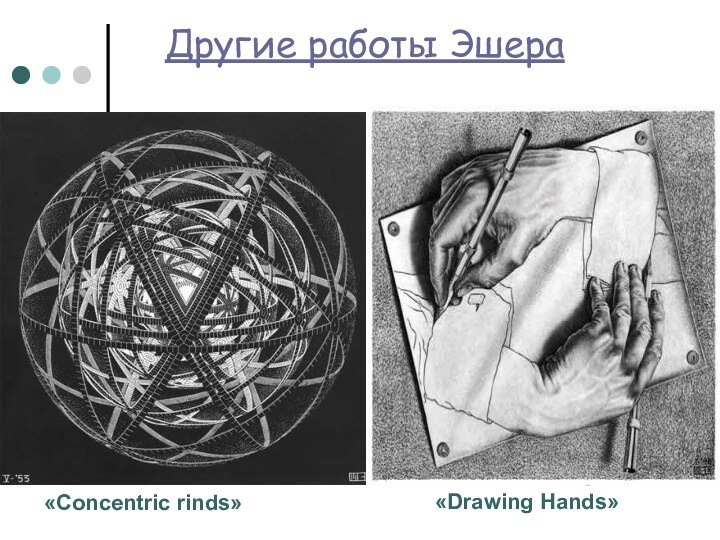
- 9. Другие работы Эшера«Concentric rinds» «Drawing Hands»
- 10. Лента Мебиуса 2 1963.продольная гравюра, Замкнутая
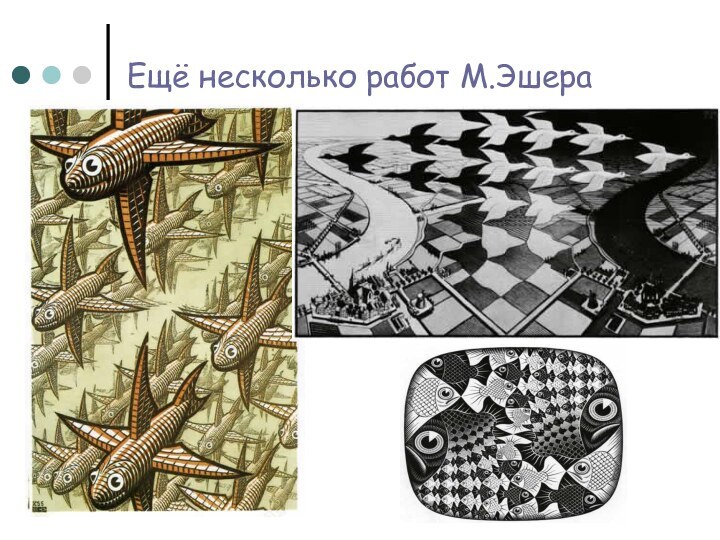
- 11. Ещё несколько работ М.Эшера
- 12. «Ascending and descending»
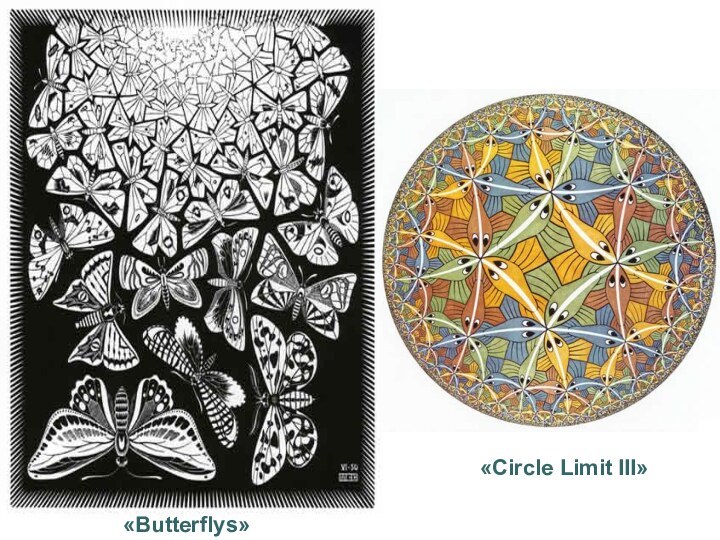
- 13. «Circle Limit III» «Butterflys»
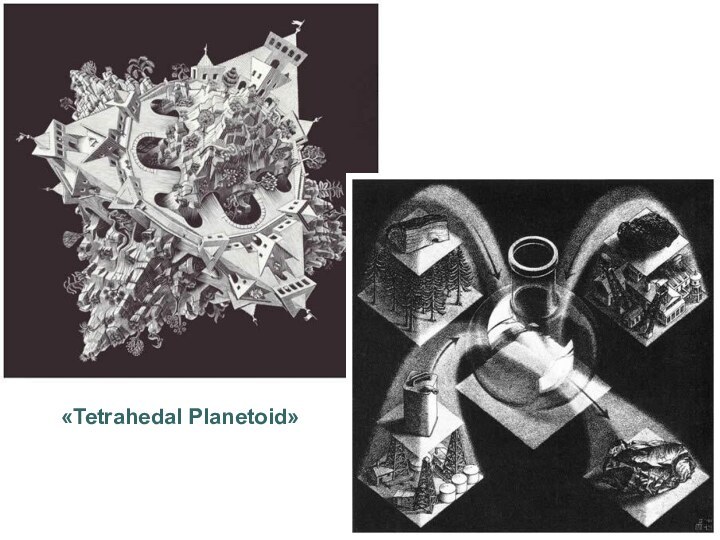
- 14. «Tetrahedal Planetoid»
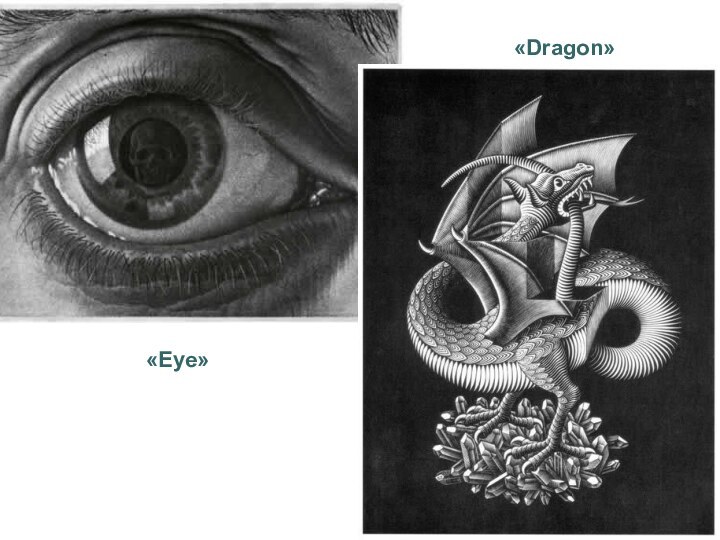
- 15. «Dragon» «Eye»
- 16. Перед нами – совершенно невозможное целое,
- 17. Четырёхугольная планетаЭта малая планета, населенная людьми, имеет
- 18. Использованные источникиВ работе использованы материалы глобальной сети InternetМатериалы Большого Энциклопедического СловаряРусско-английский словарь
- 19. Скачать презентацию
- 20. Похожие презентации
Все мои произведения — это игры. Серьезные игры. М. Эшер"Если мы создаем мир, то пусть он будет не абстрактным и туманным. Пусть он будет представлен конкретными узнаваемыми вещами."













Слайд 2 Все мои произведения — это игры. Серьезные игры. М.
Эшер
абстрактным и туманным. Пусть он будет представлен конкретными узнаваемыми вещами."
Слайд 4
«Порядок и хаос»
Звездный додекаэдр (двенадцатигранник) , расположенный в
центре, как мыльным пузырем, накрыт прозрачной сферой. В этом
символе порядка и красоты отражается хаос в виде гетерогенного собрания ненужных, разбитых и сплющенных предметов.
Слайд 5
М. Эшер о себе:
«Я так ни разу и
не смог получить хорошей оценки по математике. Забавно, что
я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти ученые люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен».
Слайд 6
Многогранники
Правильные геометрические тела - многогранники - имели
особое очарование для Эшера. Во его многих работах многогранники
являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона.
Это - тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями.
Слайд 7
О картине:
Большое количество различных многогранников может быть получено
объединением правильных многогранников, а также превращением многогранника в звезду.
Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника.Изящный пример звездчатого додекаэдра можно найти в работе "Порядок и хаос". В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Необычная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.
Заметим также, что анализируя картину можно догадаться о природе источника света для всей композиции - это окно, которое отражается левой верхней части сферы.
Слайд 8
О других работах с многогранниками
Фигуры, полученные объединением правильных
многогранников, можно встретить во многих работах Эшера. Наиболее интересной
среди них является гравюра "Звезды", на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры.Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.
Слайд 10
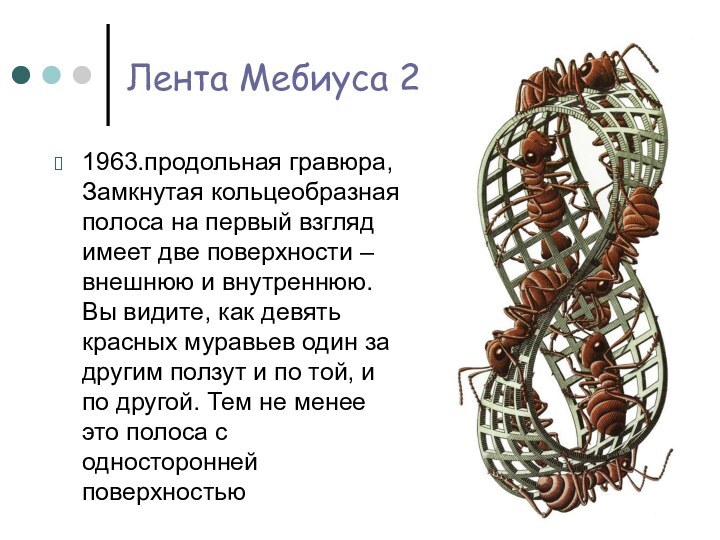
Лента Мебиуса 2
1963.продольная гравюра, Замкнутая кольцеобразная
полоса на первый взгляд имеет две поверхности – внешнюю
и внутреннюю. Вы видите, как девять красных муравьев один за другим ползут и по той, и по другой. Тем не менее это полоса с односторонней поверхностьюСлайд 16 Перед нами – совершенно невозможное целое, поскольку
в интерпретации расстояния между объектом и наблюдателем возникают неожиданные
изменения. Падающая вода приводит в движение мельничное колесо и течет по наклонному зигзагообразному желобу между двумя башнями, возвращаясь к точке, где водопад начинается снова. Кажется, что обе башни одинаковой высоты; но тем не менее, та что справа, оказывается этажом ниже, чем башня слева«Towers»
Слайд 17
Четырёхугольная планета
Эта малая планета, населенная людьми, имеет форму
правильного четырехгранника и окружена сферической атмосферой. Видны 2 из
4 грани тетраэдра; ребро делит изображение надвое. Все вертикальные линии: стены домов, деревья и люди – направлены к центру тяжести, а все горизонтальные поверхности: сады, улицы, крыши, вода прудов и каналов – составляют часть сферической оболочки.«Tetrahedal Planetoid»