Слайд 2
Введение
Рабочая программа факультативного курса «Решение задач с параметрами»

в 8 классе разработана на основе:
Федерального закона от 29.12.2012
N 273-ФЗ (ред. от 23.07.2013)
«Об образовании в Российской Федерации».
Федерального компонента государственного стандарта общего образования. Приказ Минобразования РФ от 05.03.2004 N 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования».
Приказа Министерства образования и науки Российской Федерации (Минобрнауки России) Приказом от 31 марта 2014 г. № 253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования».
Мирошин В.В. Решение задач с параметрами. Теория и практика/В.В. Мирошин.- М.:Издательство «Экзамен»2009-286
Данные программы полностью отражают базовый уровень подготовки школьников
Слайд 3
Актуальность.
Согласно ФГОС ООО выпускник школы должен быть способным
к осуществлению учебно-исследовательской деятельности. Именно задачи с параметрами дают
большой размах поисковой деятельности, возможность обсуждать и доказывать, позволяют проверить знания основных разделов школьного курса математики, уровень логического мышления, первоначальные навыки исследовательской деятельности. Именно задачи с параметрами открывают перед учениками большое количество эвристических приемов общего характера, ценного для математического развития личности.
Слайд 4
Актуальность.
Однако использование учебника с углубленным изучением математики не
всегда возможно в условиях обычной школы, поэтому существует потребность
в дополнительном обучении детей на факультативных занятиях по теме «Решение задач с параметром».
Задачи, предлагаемые в данном курсе, рассматриваются по принципу от простого к сложному, переход от репродуктивного уровня усвоения материала к творческому.
Программа курса построена таким образом, что каждое занятие включает в себя теоретические знания, постановку проблемы, выдвижение и проверку гипотез, поиск решения. Все темы дополняют, расширяют и углубляют знания учащихся.
.
Слайд 5
Актуальность.
Изучение физических, химических, экономических и многих других закономерностей
часто приводит к решению задач с параметрами, к исследованию
процесса в зависимости от параметра. Поэтому навыки решения задач с параметрами, знание некоторых их особенностей нужны всем специалистам, в любой области научной и практической деятельности.
Слайд 6
Цели реализации программы:
Формирование у учащихся умения и навыков
по решению задач с параметрами, сводящихся к исследованию линейных
и квадратных уравнений, неравенств.
Формирование у учащегося интереса к предмету, развитие математических способностей.
Формирование у учащихся навыка исследовательской деятельности.
Расширение и углубление знаний, подготовка их к осознанному выбору профиля обучения в старшей школе.
Организационно-педагогические основы обучения.
Программа рассчитана на 1 год.
Возраст обучающихся 8 класс.
Режим работы: 1 раз в неделю по 1 часу (45 минут).
Всего в течение года 34 часа.
Слайд 7
В рамках указанного курса решаются следующие задачи:
овладение
системой математических знаний и умений, необходимых для применения в
практической деятельности, изучения смежных дисциплин, продолжения образования;
формирование интеллекта, а также личностных качеств, необходимых человеку для полноценной жизни, развиваемых математикой: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание отношения к математике как к части общечеловеческой культуры, формирование понимания значимости математики для научно-технического прогресса.
Слайд 8
Методы и формы обучения
Выбор методов и форм
обучения курсу алгебры в 8 классе основан на сформулированных
выше задачах.
Среди основных методов обучения выделяем следующие: самостоятельной работы, визуализации, математического моделирования, исследования, ИКТ, элементы электронного обучения и мозгового штурма др.
В процессе преподавания курса важным компонентом являются средства обучения:
печатные пособия (учебники, раздаточный и дидактический материалы);
наглядные пособия (плакаты, графики, таблицы);
электронные образовательные ресурсы (мультимедийные средства обучения).
Слайд 9
Методы и формы обучения
При планировании курса учтена возможность
включения разнообразного иллюстративного материала, мультимедийных и интерактивных моделей, использование
компьютерной информационной базы для организации самостоятельной работы школьников при повторении теоретического материала и тестирования для проверки и контроля знаний
Слайд 10
Методы и формы обучения
В основе образовательной программы лежит
классно-урочная система (индивидуальная, групповая, индивидуально-групповая, фронтальная). Так же предполагается
использование нетрадиционных форм уроков, таких как:
урок – коммуникации;
урок – практикум;
урок – игра;
урок – ИКТ;
урок – исследование;
урок – консультация;
урок – творчество;
Слайд 11
Методы и формы обучения
Очные семинары и занятия по
приглашению, интернет-ресурсы.
Так же применяются технологии:
Уровневой дифференциации;
Здоровьесберегающие технологии;
Технологии развития
критического мышления.
Технология групповой работы
Технология проблемного обучения.
Технология проектной деятельности.
Технология развития критического мышления.
Игровые технологии.
Технология уровневой дифференциации обучения.
Технология обучения на основе учебных ситуаций.
Информационно-коммуникационные технологии.
Технология интерактивного обучения.
Технология индивидуализации обучения.
Слайд 12
Содержательный компонент.
Содержательный компонент образовательной программы составляем на основе
принципов:
соответствие целям (при отборе учебного материала, направленного на получение
нового результата математической подготовки учащихся 7 классов по алгебре, ориентируемся на структуру целевого компонента. обеспечиваем предмет учебной деятельности составляющими, адекватными составу предметных, метапредметных и личностных целевых компонентов);
дидактическая достаточность (объем учебного материала должен быть достаточен для достижения требуемого результата каждому учащемуся);
преемственность (содержание курса базируется на курсе алгебры 7 класса, развивая его в формате ФГОС, каждый последующий модуль логично взаимосвязан с предыдущими в содержательном и организационном аспектах)
Слайд 13
Содержательный компонент.
Содержательный компонент разработан на основе пособия Мирошина
В.В. Решение задач с параметрами. Теория и практика и
представлен в виде 4 модулей.
Модуль: Линейные уравнения с параметрами.
Задачи с параметром. Первое знакомство. Типы задач с параметрами. Что значит - решить уравнение или неравенство с параметрами. Что значит - исследовать уравнение(определить количество решений, найти положительные решения и т.д.), содержащее параметры. Общие подходы к решению линейных уравнений. Алгоритм решения линейных уравнений с параметром. Решение уравнений приводимых к линейным.
Слайд 14
Содержательный компонент.
Построение графиков линейных уравнений содержащих модуль. Решение
линейных уравнений содержащих модуль f│x│=a, │f(x)│=a, │f(x)│=g(x), │f(x)│=│g(x)│. Уравнения
теплового баланса. Построение функции спроса(линейной). Построение графика равномерного движения.
Модуль: Дробно-линейные уравнения с параметрами. Системы линейных уравнений с параметрами.
Дробно-линейные уравнения. Область определения. Метод интервалов при решении дробно-линейных уравнений с параметрами. Параметр и количество решений систем линейных уравнений. Решение систем линейных уравнений с параметрами.
Слайд 15
Содержательный компонент.
Модуль: Квадратные уравнения с параметрами.
Свойства квадратного трехчлена.
Алгоритм решения квадратных уравнений с параметром. Общее решение квадратного
уравнения с параметрами (« для каждого значения параметра найти все решения уравнения»). Решение квадратного уравнения с условием(« найти все значения параметра при каждом из которых уравнение удовлетворяет заданным условиям»). Применение теоремы Виета при решении квадратных уравнений с параметрами. Использование симметрии в аналитических выражениях. Использование графических иллюстраций в задачах с параметрами. Задачи на нахождение количества теплоты.
Построение функции описывающей траекторию тела брошенного вертикально вверх.
Слайд 16
Содержательный компонент.
Модуль: Линейные и квадратные неравенства
с параметрами.
Решение линейных неравенств с параметрами вида ax≤b, ax≥b.Решение
квадратных неравенств с параметрами.
Слайд 17
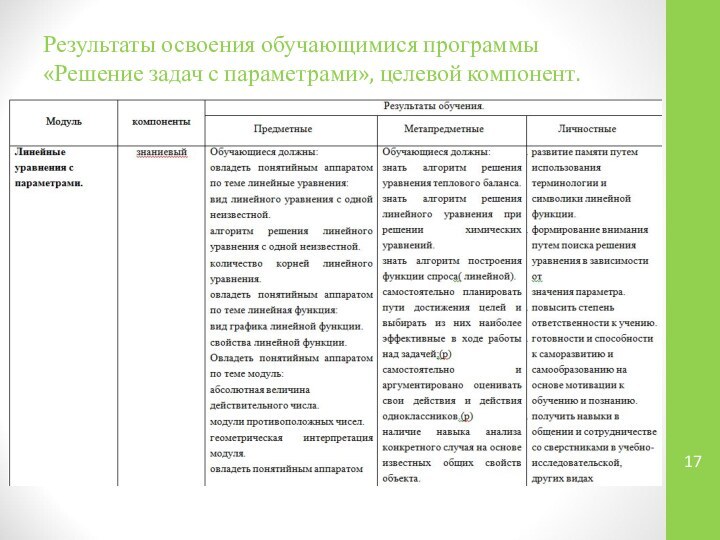
Результаты освоения обучающимися программы «Решение задач с параметрами»,
целевой компонент.
Слайд 18
Результаты освоения обучающимися программы «Решение задач с параметрами»,
целевой компонент.
Слайд 19
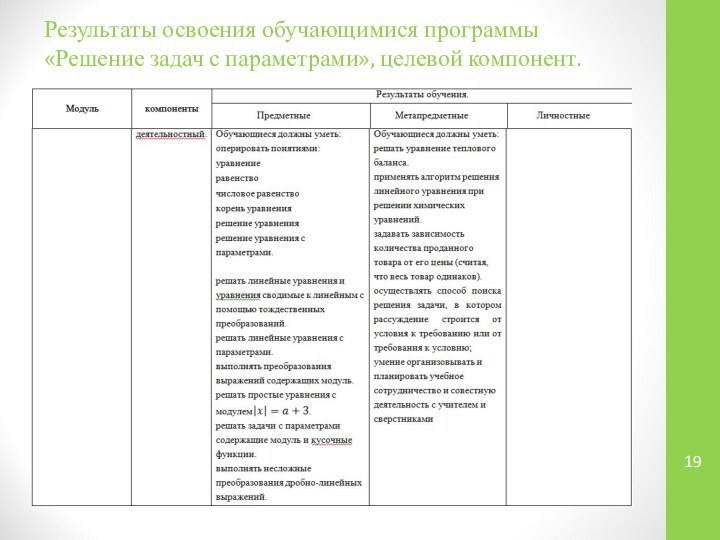
Результаты освоения обучающимися программы «Решение задач с параметрами»,
целевой компонент.