- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Наибольшее и наименьшее значение функции
Содержание
- 2. Через математические знания лежит широкая дорога к огромным, почти необозримым областям труда и открытий.Маркушевич А.И.
- 3. Цели урока:
- 4. ХMAX=1, ХMIN=-1
- 5. «Дешифратор»
- 7. Вопрос: какую наибольшую площадь земли могли купить финикийцы?
- 8. Задача. Одна сторона прямоугольного участка земли
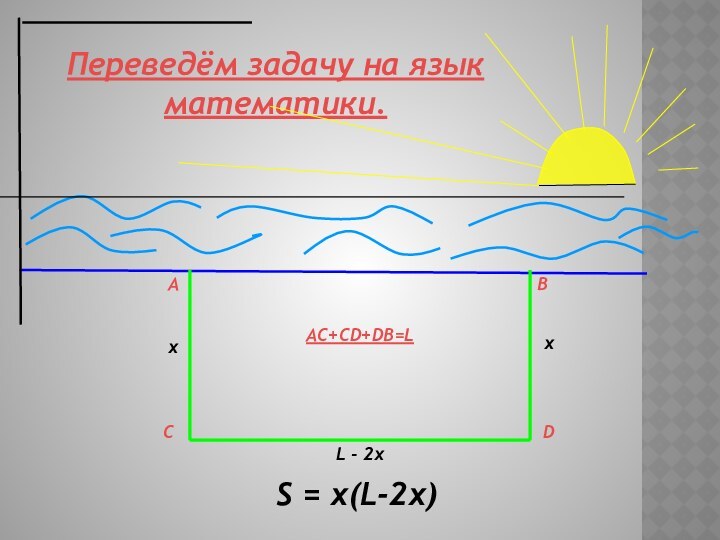
- 9. ABCDAC+CD+DB=LxxL - 2xПереведём задачу на язык математики.S = x(L-2x)
- 10. РЕШЕНИЕ:ЗАДАДИМ ФУНКЦИЮS(X)=X*(600-2X)=600X-2X²НАЙДЕМ ПРОИЗВОДНУЮS‘(X)=600-4XНАЙДЕМ СТАЦИОНАРНЫЕ ТОЧКИS’(X)=0600-4X=0-4X=-600X=150НАЙДЕМ ЗНАЧЕНИЕ ФУНКЦИИ ПРИ Х=150S(150)=150*(600-2*150)=4500 (м²)
- 11. «Много ли человеку земли нужно» Фрагмент рассказа
- 12. Фигура, которая получилась у Пахома, изображена на
- 13. Составим математическую модель:a – первая сторона, 20
- 14. Выводы 1.Если
- 15. Для стоянки машин выделили площадку
- 16. Окно имеет форму прямоугольника, периметр которого равен
- 17. Алгоритм нахождения наибольшего и наименьшего значения функции
- 18. Из прямоугольного листа жести размером 25 х 40 см надо изготовить открытую коробку наибольшего объема.
- 19. Решение. Обозначим сторону вырезаемых по углам квадратов через
- 20. Решение экзаменационных заданий:
- 21. Задание 1 Найти наибольшее и наименьшее значение
- 22. Скачать презентацию
- 23. Похожие презентации




















Слайд 2 Через математические знания лежит широкая дорога к огромным,
почти необозримым областям труда и открытий.
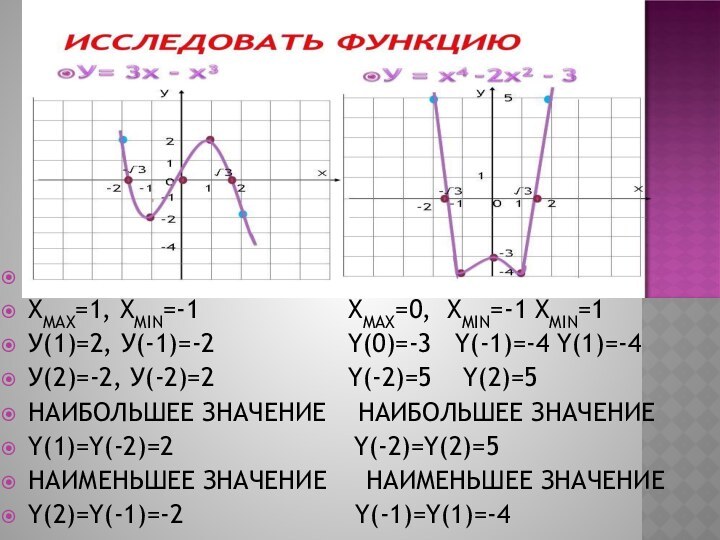
Слайд 4
ХMAX=1, ХMIN=-1
ХMAX=0, ХMIN=-1 XMIN=1
У(1)=2, У(-1)=-2
Y(0)=-3 Y(-1)=-4 Y(1)=-4У(2)=-2, У(-2)=2 Y(-2)=5 Y(2)=5
НАИБОЛЬШЕЕ ЗНАЧЕНИЕ НАИБОЛЬШЕЕ ЗНАЧЕНИЕ
Y(1)=Y(-2)=2 Y(-2)=Y(2)=5
НАИМЕНЬШЕЕ ЗНАЧЕНИЕ НАИМЕНЬШЕЕ ЗНАЧЕНИЕ
Y(2)=Y(-1)=-2 Y(-1)=Y(1)=-4
Слайд 8 Задача. Одна сторона прямоугольного участка земли примыкает к
берегу моря, а три другие огораживаются ремнем, длина которого
600м. Каковы должны быть стороны этого участка, чтобы его площадь была наибольшей?
Слайд 10
РЕШЕНИЕ:
ЗАДАДИМ ФУНКЦИЮ
S(X)=X*(600-2X)=600X-2X²
НАЙДЕМ ПРОИЗВОДНУЮ
S‘(X)=600-4X
НАЙДЕМ СТАЦИОНАРНЫЕ ТОЧКИ
S’(X)=0
600-4X=0
-4X=-600
X=150
НАЙДЕМ ЗНАЧЕНИЕ ФУНКЦИИ ПРИ
Х=150
S(150)=150*(600-2*150)=4500 (м²)
Слайд 11
«Много ли человеку земли нужно»
Фрагмент рассказа Л.Н.
Толстого «Много ли человеку земли нужно» о крестьянине Пахоме,
покупавшем землю у башкир.- А цена какая будет? – говорит Пахом.
- Цена у нас одна: 1000 рублей за день.
Не понял Пахом.
- Какая же это мера – день? Сколько в ней десятин будет?
- Мы этого, – говорит, - не умеем считать. А мы за день продаем; сколько обойдешь за день , то твое, а цена 1000 рублей.
Удивился Пахом.
- Да ведь это, - говорит, - в день обойти земли много будет.
Засмеялся старшина.
- Вся твоя, - говорит. – Только один уговор: если назад не придешь в день к тому месту, с какого возьмешься, пропали твои деньги.
Слайд 12
Фигура, которая получилась у Пахома, изображена на рисунке
Р=40
км
S=(a+b)/2*h
S=(2+10)/2*13=78 (км²)
Проверим, наибольшую ли площадь при этом получил бы
Пахом (с учетом того, что участки обычно имеют форму прямоугольника)?
Слайд 13
Составим математическую модель:
a – первая сторона,
20 –
а – вторая сторона
S = а (20 - а)
= - а² + 20 а.S´ = - 2а + 20 = 0,
а = 10.
S=10*(20-10)=100 (км²)
Р = 40 км.
наибольший четырехугольник – квадрат, т.е. наибольшая площадь – 100 м².
Слайд 14
Выводы
1.Если функция непрерывна на отрезке, то она достигает
на нем и своего наибольшего, и своего наименьшего значений.
2.Наибольшего
и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.3.Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
1.Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего, и своего наименьшего значений.
2.Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3.Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Выводы
Слайд 15 Для стоянки машин выделили площадку прямоугольной
формы, примыкающую одной стороной к стене здания. Площадку обнесли
с трех сторон металлической сеткой длиной 200 м, и площадь ее при этом оказалась наибольшей. Каковы размеры площадки?L=200 м
а-длина стороны
ограждения;
в-другая сторона
S=а*в- площадь прямоугольника
в-?
Слайд 16 Окно имеет форму прямоугольника, периметр которого равен 8
м. Каковы должны быть размеры окна, чтобы оно пропускало
наибольшее количество света?Р=8 м
а-?
в-?
Слайд 18 Из прямоугольного листа жести размером 25 х 40
см надо изготовить открытую коробку наибольшего объема.
Слайд 19
Решение.
Обозначим сторону вырезаемых по углам квадратов через х.
Дном коробки является прямоугольник, стороны которого равны а =
25 – 2х и в = 40 – 2х.Высота коробки равна х.
V = (25 – 2х)(40 – 2х)х, т.е. является функцией от переменной х.
у = (25 – 2х)(40 – 2х)х = 4х3 – 130х2 + 1000х
ОДЗ: (0; 12,5).
Найдем экстремумы этой функции.
у' = (4х3 – 130х2 + 1000х)' = 12х2 – 260х + 1000
12х2 – 260х + 1000 = 0
Критические точки функции х=162/3 – не входит в область определения функции.
Х2 = 5
V(5) = 2250см3.
Слайд 21 Задание 1 Найти наибольшее и наименьшее значение функции у
= х³ - 3х² - 45х + 1 на
[-4; 6] без построения графика. Задание 2 Рекламный щит имеет форму прямоугольника S = 9 м². Изготовьте щит в виде прямоугольника с наименьшим периметром.Домашнее задание: