Презентация на тему Открытый урок по математике в 9 классе Готовимся к ОГЭ. Решение текстовых задач

подобно плаванию, или катанию на коньках, или игре на

фортепиано: научиться этому можно, лишь подражая избранным образцам и постоянно тренируясь»
Д. Пойа

не только определенной подготовки, но также некоторой активизации мышления.

Задачи из второй части Модуль алгебра недаром относятся к задачам повышенной сложности. Для текстовых задач не существует единого алгоритма решения – в этом вся их сложность. Тем не менее существуют типовые задачи, которые вполне решаются стандартно. Наиболее распространенный, довольно эффективный способ использования таблиц. В зависимости от типа решаемой задачи столбики в таблице будут иметь разные названия.

Решение текстовых задач

решения есть процесс изобретательства. Классификация текстовых задач
Задачи на

движение.
Задачи на смеси и сплавы.
Задачи на проценты.
Задачи на работу.

обобщить и систематизировать знания

Задачи урока:
рассмотреть задачи на работу и движение;
обратить внимание на схематизацию и моделирование условия задач;
отработать основные этапы решения текстовых задач.

а скорость течения 4,7км/ч. Найдите скорость катера по течению

и против течения.
2. Найдите 5% от числа 40.
3. Периметр квадрата 4,8 см. Найдите его сторону и площадь.
4. Какой путь пройдет турист со скоростью 4,5км/ч за 3 часа?
5. За 45 мин. мастер изготовил 15 деталей.
Сколько деталей изготовит мастер за час?

время, в течение которого производится работа,
производительность труда, работа, произведенная

в единицу времени
работа, произведенная за время t

Задачи на движение обычно содержат
следующие величины:
– время,
– скорость,
– расстояние.
Уравнения, связывающие эти три величины:

Задачи на движение

Задачи на работу

объёма работы, за 1 прими
Данные в таблицу занеси
Уравнение запиши
Уравнение

реши!

Что необходимо делать?

в минуту меньше, чем вторая труба. Сколько литров в

минуту пропускает первая труба, если бассейн объёмом 480 литров она заполняет на 20 минуты дольше, чем вторая труба?

 

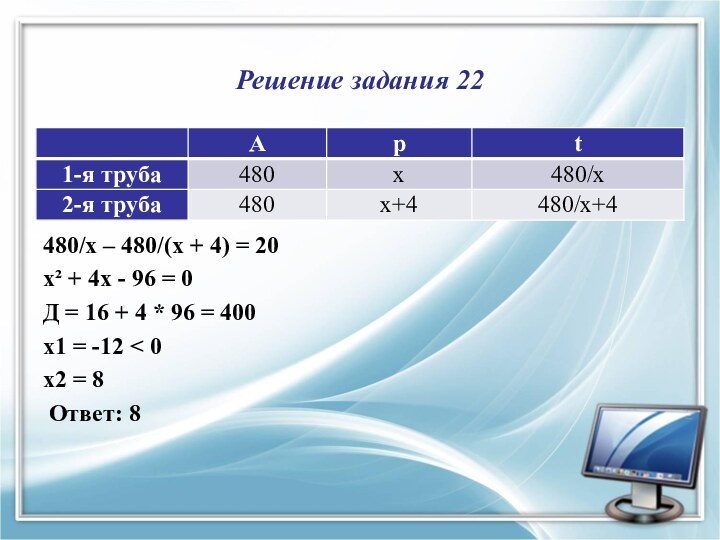
1 труба

2 труба

20
х² + 4х - 96 = 0
Д = 16

+ 4 * 96 = 400
х1 = -12 < 0
х2 = 8
Ответ: 8

найдите периметр и объём бассейна. Длина – 16м, ширина

– 10м, высота – 3 м.
2. Най­ди­те сум­мар­ную пло­щадь бо­ко­вых стен и дна бас­сей­на (в квад­рат­ных метрах).
Решение:
Sбок=(16*3+10*3)*2=156
Sдна=16*10=160
S=156+160=316 м²

заполняющих бассейн объёмом 480 литров. На сколько минут быстрее

одна из труб заполнит бассейн?

Найдите сумму первых пяти её членов.
Решение:
120, 240, 360,

480, …
a1=120, d=120, а5=600
S5=(120+600)*5/2=1800
2) 10, 20, 30, 40, …
a1=10, d=10, а5=50
S5=(10+50)*5/2=150

AB=8 и ∟А=30°.
Найдите площадь треугольника АВС.
Найдите площадь трапеции

MNBC.

M

N

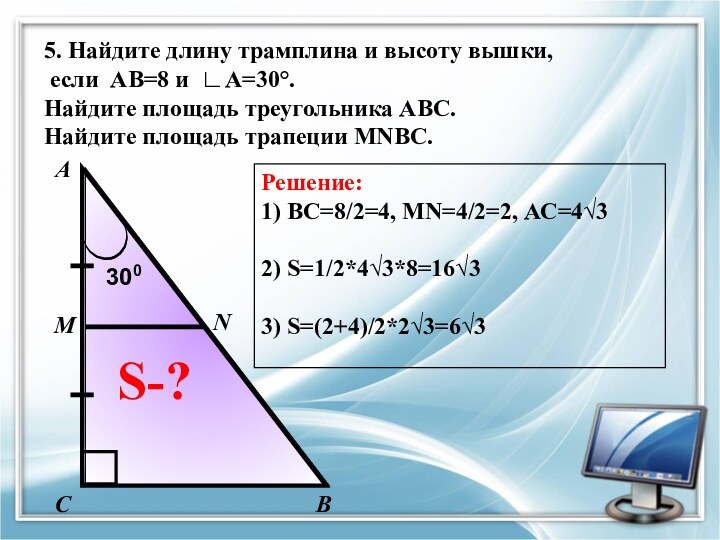
Решение: 1) ВС=8/2=4, MN=4/2=2, АС=4√3

2) S=1/2*4√3*8=16√3

3) S=(2+4)/2*2√3=6√3

20 задач за то время, за которое Маша может

решить в 2 раза меньше задач. Саша и Маша вместе могут решить 20 этих задач за 2 ч. За сколько часов Саша самостоятельно может решить 20 задач?

Задание 22/1

Cаша

Маша

t

х

20

А

10

р

х

2

вместе

20

Составим и решим

уравнение.

Ответ: 3 ч.

вместе изготавливают 50 деталей. Ученику для изготовления 50 деталей

требуется времени на 2 часа больше, чем требуется токарю для изготовления 120 деталей. Сколько деталей в час изготовляет токарь?

Задание 22/2

токарь

ученик

р

х

120

A

50

t

Составим и
решим уравнение.

Ответ: 40 деталей
в час.

вместе

50

х+2

5х2 – 7х – 24 = 0

х = 3

=3

заказ за 12 часов, а другой – за 18

часов. За сколько часов выполнят заказ эти мастера, работая вместе?

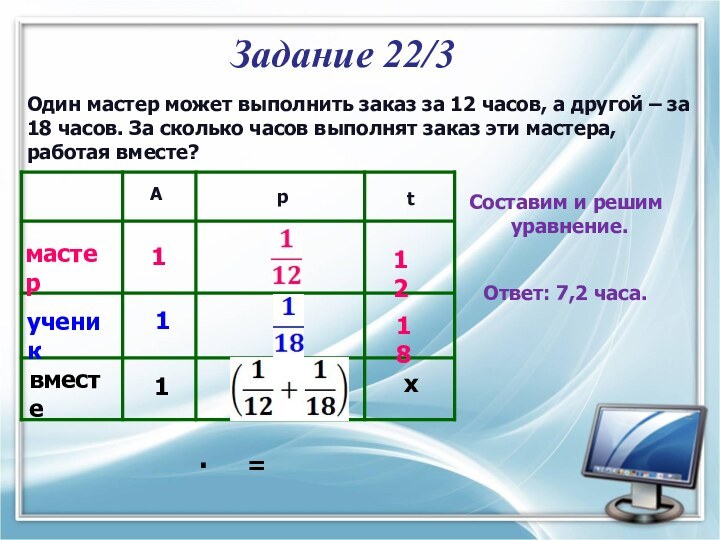
Задание 22/3

мастер

ученик

t

12

1

А

1

р

18

х

вместе

1

Ответ: 7,2 часа.

.

=

Составим и решим
уравнение.

за 36 часов, первая и третья – за 30

часов, вторая и третья – за 20 часов. За сколько часов наполнят бассейн три трубы, работая вместе?

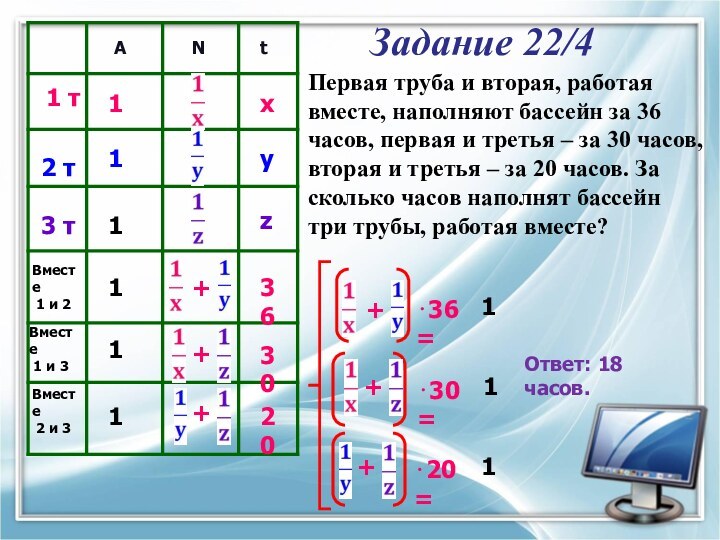
Задание 22/4

1 т

2 т

х

1

1

у

z

Вместе
1 и 2

1

Ответ: 18 часов.

3 т

36

1

Вместе
1 и 3

1

Вместе
2 и 3

1

30

20

⋅36=

1

⋅30=

1

⋅20=

1

А

N

t

способа решения.
Моделирование отношений.
Осуществление способа (решение).
Рефлексивный анализ использованного средства.