Слайд 2
Укажите номера верных утверждений:
Вписанный угол, опирающийся на диаметр,
прямой.
Вписанным называется угол, вершина которого лежит в окружности.
Вписанный угол
измеряется величиной дуги, на которую он опирается.
Центральным называется угол, вершина которого лежит в центре окружности.
Вписанный и центральный углы, опирающиеся на одну и ту же дугу равны.
Слайд 5
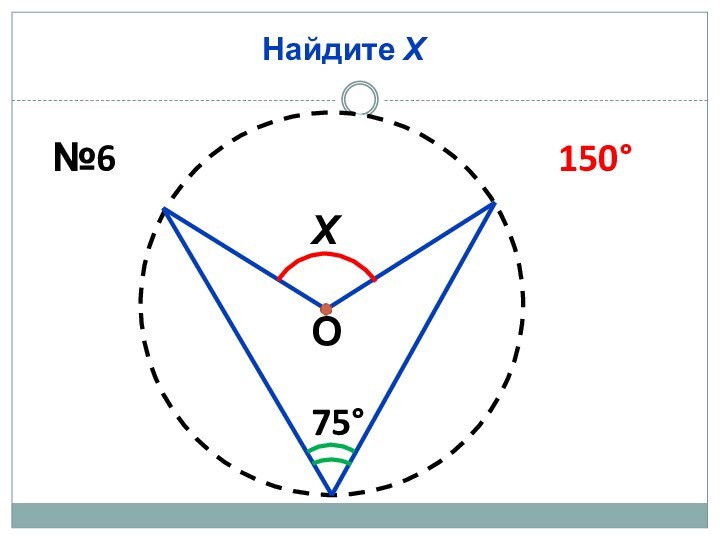
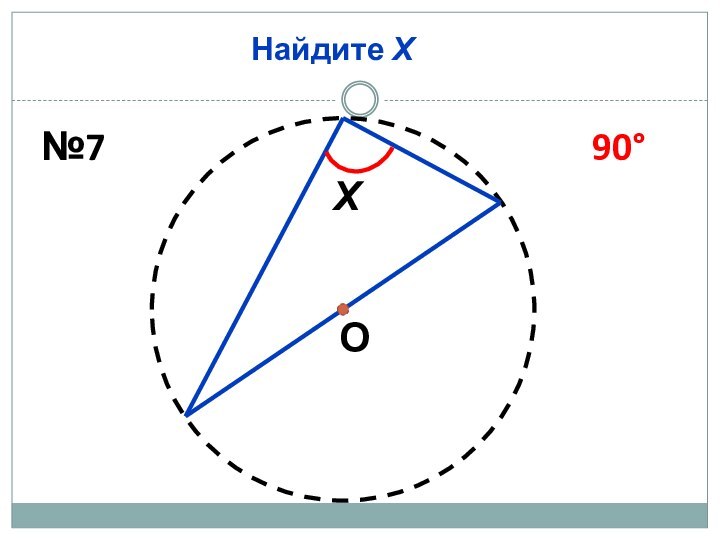
Найдите Х
Х
75
№3
О
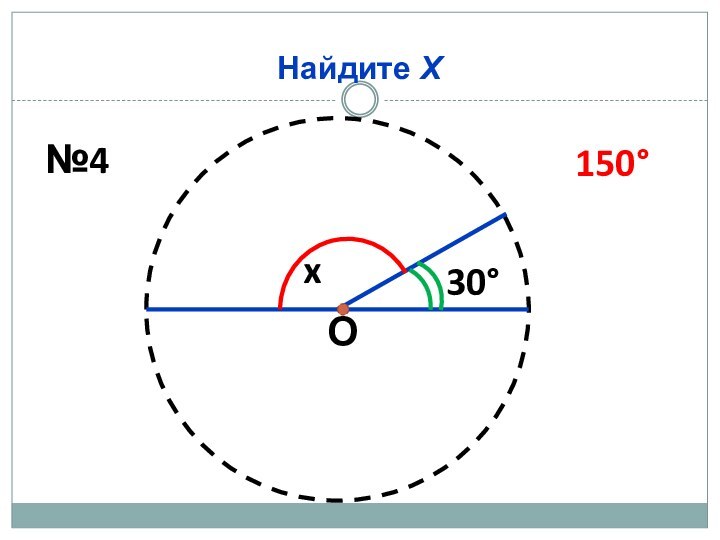
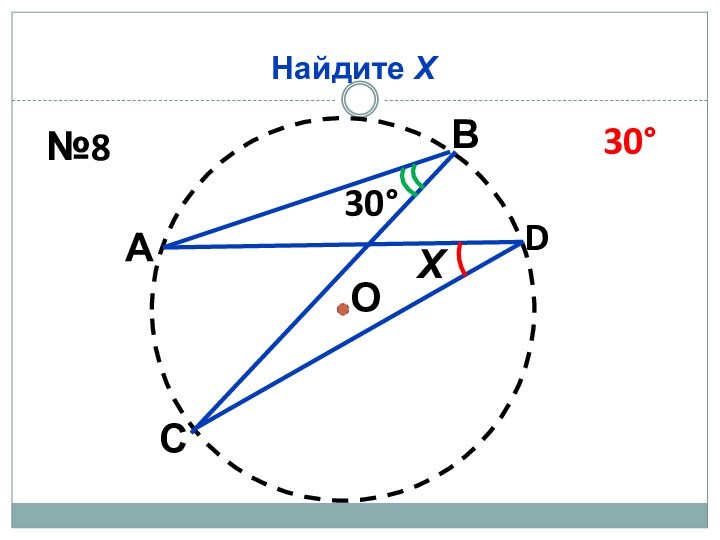
Найдите Х
150
Слайд 11
Проблема № 1:
Как быстро циркулем и
линейкой
построить сразу несколько углов
равных данному ?
Слайд 12
А
В
С
Построение угла, равного данному.
Дано: __А.
Построить: __ О =
__ А
О
D
E
Слайд 13
Проблема № 1 ?
Следствие 1:
Вписанные углы, опирающиеся на
одну и ту же дугу, равны.
Слайд 14
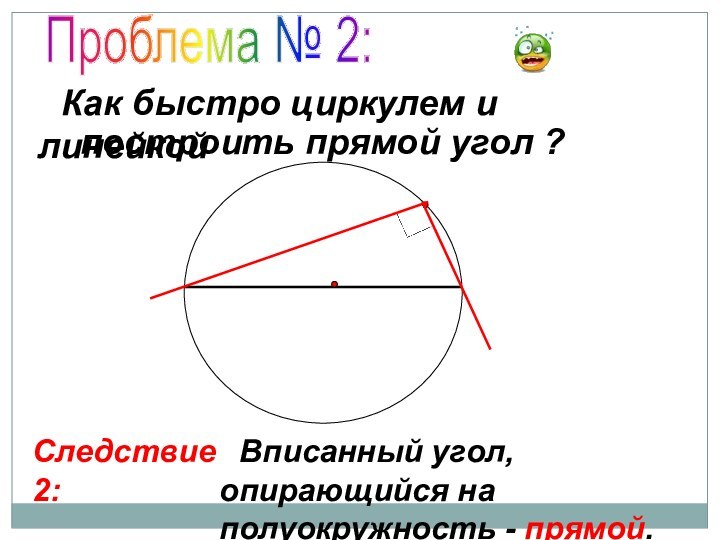
Проблема № 2:
Как быстро циркулем и
линейкой
построить прямой угол ?
Слайд 15
В
А
Построение
перпендикулярных
прямых.
Слайд 16
Проблема № 2:
Как быстро циркулем и
линейкой
построить прямой угол ?
Следствие 2:
Вписанный угол,
опирающийся на полуокружность - прямой.
Слайд 19
1) Найдите угол NAP
2) Найдите дугу ВС
Задание 1.
угол
NAP = 40°
дуга ВС = 150°
Слайд 20
Задание 2.
1) Найти угол АВС. 2)
Найти угол АВС. 3) Найти углы А и
С.
угол АВС = 40°
угол АВС = 130°
угол А = 53°, угол С = 90°
Слайд 21
Задание 3.
1) Найти углы АОD и ACD.
2) Найти угол АВС. 3) Найти угол
ВСD.
угол АОD = 80°, угол ACD = 40°
угол АВС = 120°
угол ВСD = 110°
Слайд 22
В
32°
100°
С
E
№ 660
Через точку, лежащую вне окружности, проведены две
секущие,
образующие угол в 32°.
Большая дуга окружности, заключенная
между сторонами этого
угла, равна 100°. Найдите меньшую дугу.
О
360
Слайд 23
Тест на оптическую иллюзию по рисункам с альтернативным
ответом.
Вписанные углы
Оптическую иллюзию мы довольно часто наблюдаем и даже
применяем в нашей практике, но очень мало знаем ее сущность. Иллюзию зрения используют архитекторы при постройке зданий, модельеры при создании моделей, художники при создании декораций. Нам известно, что тело, окрашенное в светлые тона, кажется больше, чем тело того же размера, окрашенное в темный тон. Бывают причины, вызывающие оптические иллюзии.
Слайд 24
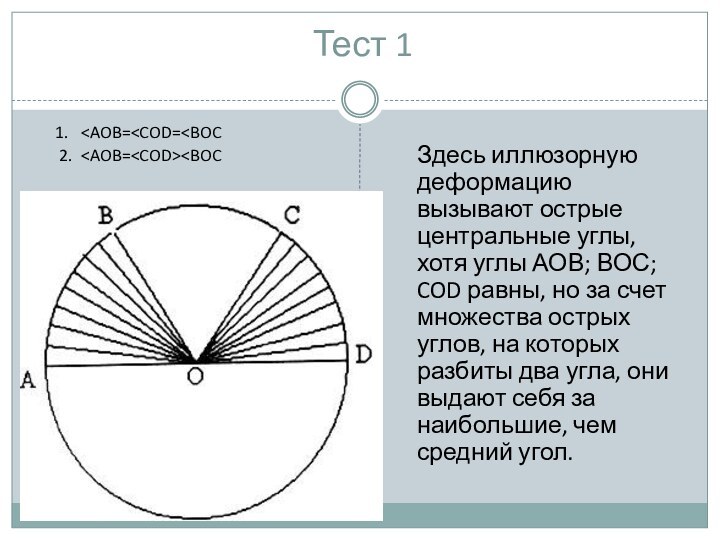
Тест 1
Вписанные углы
1.
Здесь иллюзорную деформацию вызывают острые центральные углы, хотя углы
АОВ; ВОС; COD равны, но за счет множества острых углов, на которых разбиты два угла, они выдают себя за наибольшие, чем средний угол.
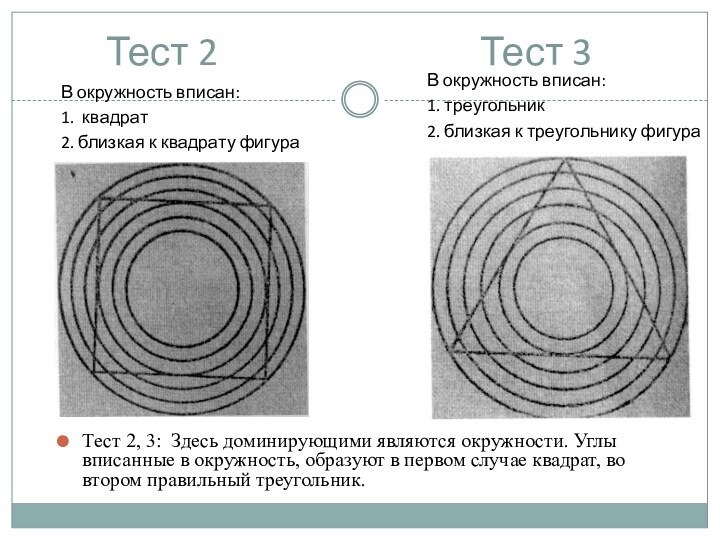
Тест 3
В окружность вписан:
1. квадрат
2. близкая к квадрату фигура
В окружность вписан:
1. треугольник
2. близкая к треугольнику фигура
Тест 2, 3: Здесь доминирующими являются окружности. Углы вписанные в окружность, образуют в первом случае квадрат, во втором правильный треугольник.
Слайд 26
Природа цвета и цвета природы
нет некрасивых цветов -
есть неподходящие
Ви́льгельм Фри́дрих О́ствальд
Для определения гармоничных цветов используются
и другие колориметрические круги: КИНК — киноварнокрасный, КОР — краснооранжевый, ЖОР — желтооранжевый, ЗОЛЖ — золотистожелтый, Ж — желтый, ЛЖ — лимонножелтый, ЖЗ — желтозеленый, ХЛ — хлорофилловый, ИЗЖ — изумрудножелтый, СРЗ — среднезеленый, СЗ — синезеленый, ЦМВ — цвет морской волны, БИР — бирюзовый, ВС — васильковосиний, С — синий, СРС — среднесиний,УЛ — ультрамариновый, СИНФ — синефиолетовый, СФ — синеватофиолетовый, Ф — фиолетовый, ПУРФ — пурпурнофиолетовый,ПУРК — пурпурнокрасный, КАРК — карминнокрасный, К — красный.
Слайд 27
Как уже было сказано раньше, цветовой круг построен
на двух контрастных парах, расположенных друг против друга (красный
- зеленый, желтый - синий).
Cуществуют гармонии контрастных цветов. Если мы проведем диаметры через центр круга, продолжим от красных до зеленых, то мы увидим, что каждому оттенку красного соответствует определенный оттенок зеленого. Но в дизайне сочетания двух цветов довольно редки.
Гармоничные сочетания цветов
Слайд 28
Гармония равностороннего треугольника
Гармония образуется сочетанием цветов, расположенных
в вершинах вписанного в круг равностороннего треугольника, у которого
одна вершина - главный цвет, а противолежащая сторона - вертикальная или горизонтальная хорда.
Гармония прямоугольного треугольника
Гармонию составляют цвета, расположенные в вершинах прямоугольных треугольников, у которых гипотенузы являются диаметрами круга, а катеты - вертикальные или горизонтальные хорды.
Рассмотрим варианты гармоничного сочетания трех цветов.
Слайд 29
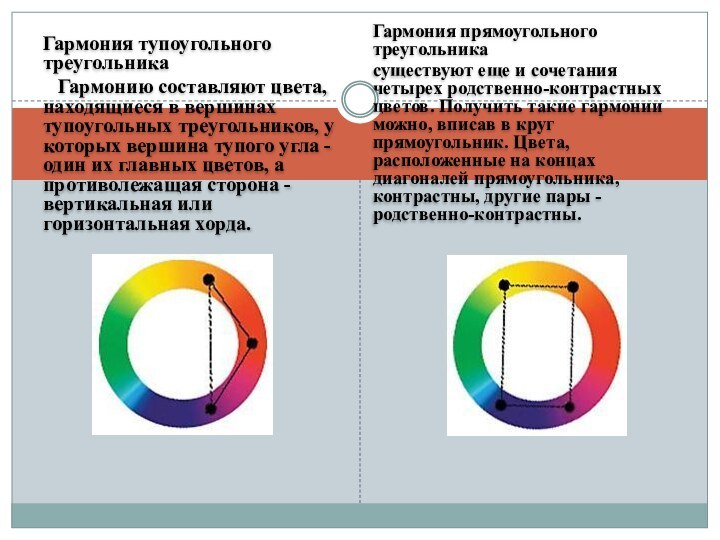
Гармония тупоугольного треугольника
Гармонию составляют цвета, находящиеся в
вершинах тупоугольных треугольников, у которых вершина тупого угла -
один их главных цветов, а противолежащая сторона - вертикальная или горизонтальная хорда.
Гармония прямоугольного треугольника
существуют еще и сочетания четырех родственно-контрастных цветов. Получить такие гармонии можно, вписав в круг прямоугольник. Цвета, расположенные на концах диагоналей прямоугольника, контрастны, другие пары - родственно-контрастны.
Слайд 32
Теория Иттена
Согласно теории Иттена, гармоничными являются сочетания трех
цветов, связанных равносторонними или равнобедренными треугольниками на схеме выбора
созвучия трех цветов.
Слайд 33
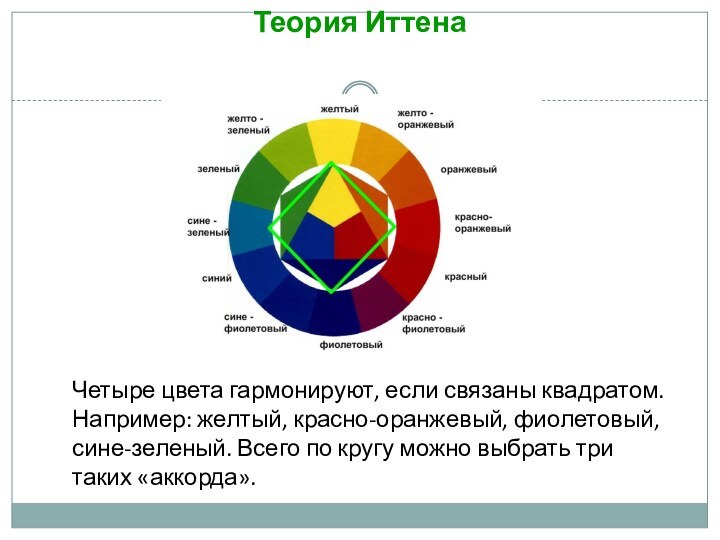
Теория Иттена
Четыре цвета гармонируют, если связаны квадратом. Например:
желтый, красно-оранжевый, фиолетовый, сине-зеленый. Всего по кругу можно выбрать
три таких «аккорда».
Слайд 35
Домашнее задание.
п. 70-71; № 662.
Творческое задание : составить
задачу по теме «Центральные и вписанные углы»