Презентация на тему по теме: Комплексные числа

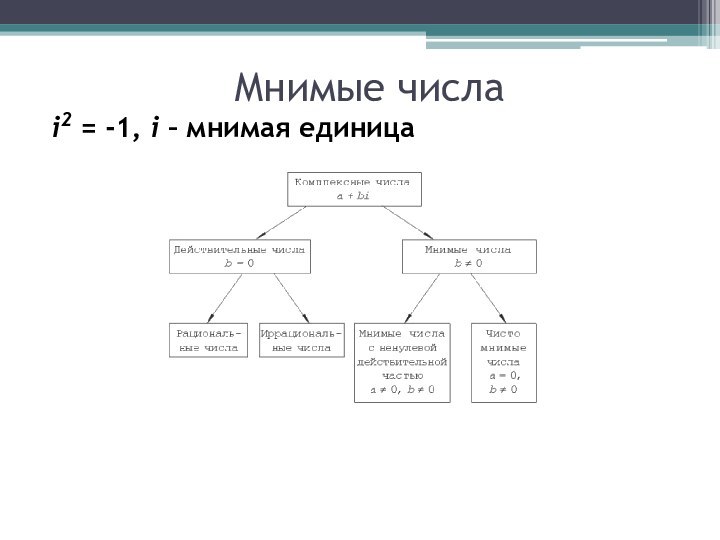
квадратный корень из , т.е. существует комплексное число, квадрат

которого равен .

2) Множество комплексных чисел содержит все действительные числа.

3) Операции сложения, вычитания, умножения и деления комплексных чисел удовлетворяют обычным законам арифметических действий (сочетательному, переместительному, распределительному).

Выполнение этих минимальных условий позволяет определить все множество С комплексных чисел.

чисто мнимого числа.


Два комплексных числа называют равными, если

равны их действительные части и равны их мнимые части:

(c + di) = (а + с) + (b

+ d)i

Вычитание:
(а + bi) - (c + di) = (а - с) + (b - d)i

Умножение:
(а + bi)·(с + di) = (ac - bd) + (ad + bc)i

сохранить действительную часть и поменять знак у мнимой части,

то получится комплексное число, сопряженное данному.

плоскости соответствует точка М(a, b).
Часто вместо точек на плоскости

берут их радиусы-векторы.
Модулем комплексного числа z = a + bi называют неотрицательное число, равное расстоянию от точки М до начала координат

числа,
r =

- модуль комплексного числа,

форме
Теорема 1. Если
и
то:
б)
а)
Теорема 2

(формула Муавра).
Пусть z — любое отличное от нуля комплексное число, п — любое целое число. Тогда