- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
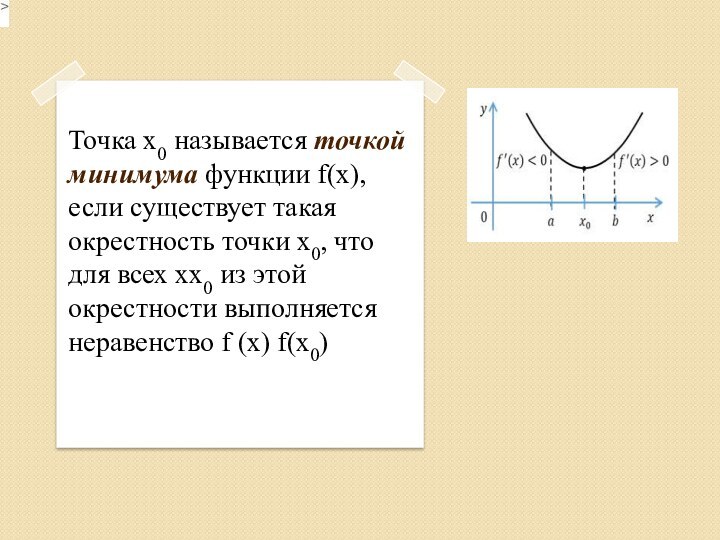
Презентация на тему по теме Применение производной к исследованию функций
Содержание
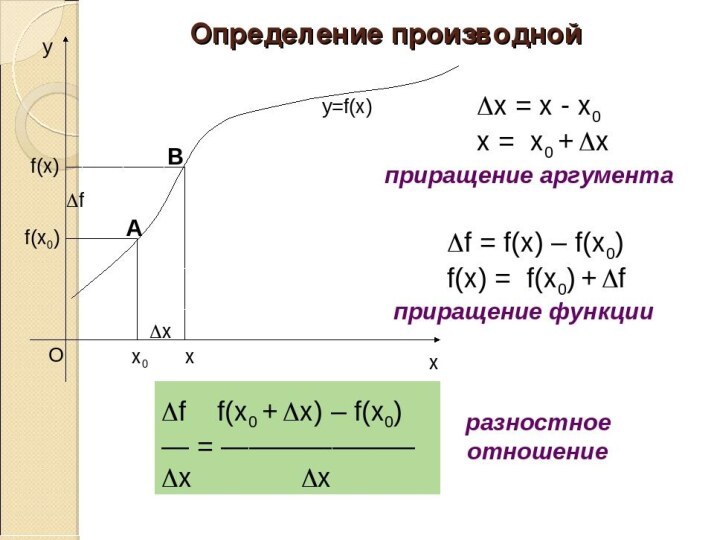
- 4. Физический смысл производной
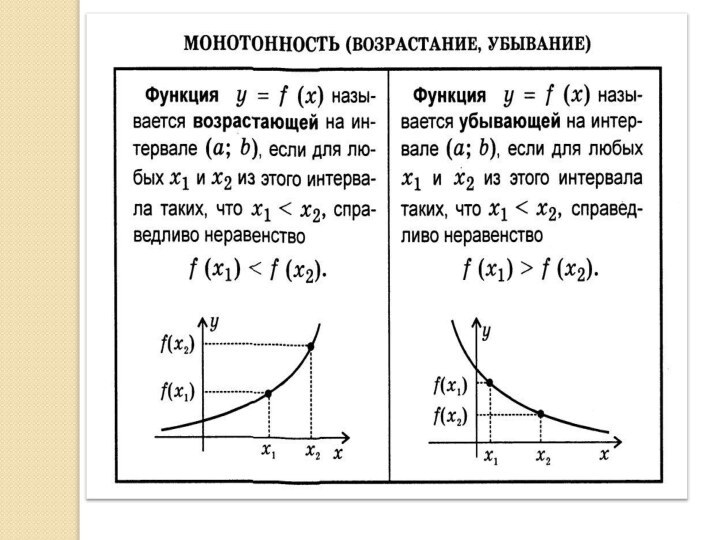
- 5. Убывающая функцияВозрастающая функция
- 8. Признаки возрастания и убывания
- 9. Алгоритм1. Указать область определения функции.Найти производную функции y=f(x).Определить промежутки, в которых f/(x) )>0 и f / (x)
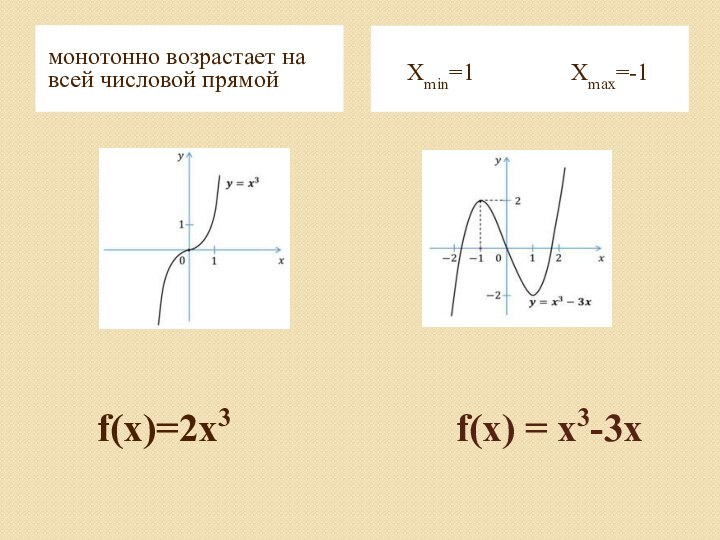
- 10. f(x)=2x3
- 14. f / (x)=0 Внутренние точки области определения функции,
- 16. Решение 2. 1. D(y)=(-oo;+oo) 2.у/=5х4-20х3+15х2=5х2(х-1)-(х-3) 3.
- 17. Задание 3.Определить область определения,промежутки монотонности функции.
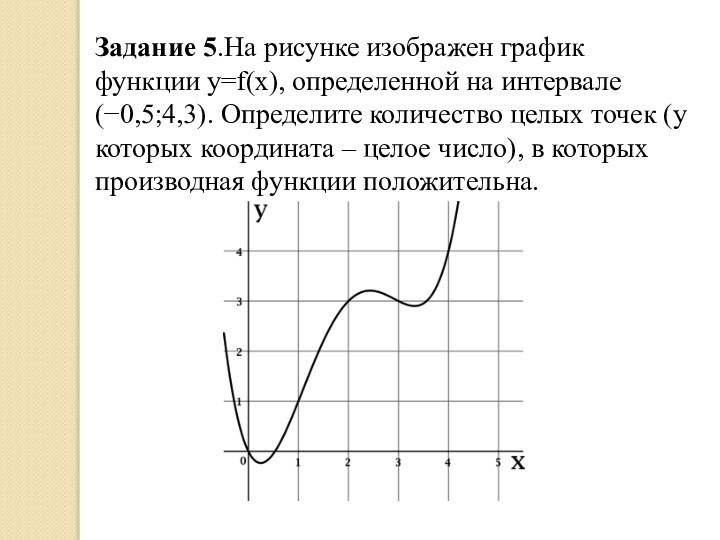
- 18. Задание 5.На рисунке изображен график функции y=f(x),
- 20. Скачать презентацию
- 21. Похожие презентации
Физический смысл производной










![Презентация по теме Применение производной к исследованию функций Решение 2. 1. D(y)=(-oo;+oo) 2.у/=5х4-20х3+15х2=5х2(х-1)-(х-3) 3. Функция возрастает на (-оо;1]u[3;+оо);](/img/tmb/13/1211847/3890fbb6806515cf0d1b28cd6619c27a-720x.jpg)





![Презентация Буква Аа. Звук [а]](/img/tmb/13/1211075/95cf91159b1d839094b3fdb6f60c15db-210x.jpg)

























