- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Приёмы решения задач по теории вероятности
Содержание
- 2. «Вероятность математическая – это числовая характеристика степени
- 3. Исходом эксперимента называют значение наблюдаемого признака, непосредственно
- 4. События бывают детерминированные (солнце встает), и случайные
- 5. Под испытанием (опытом) в теории вероятностей принято понимать наблюдение
- 6. Частота события – сколько раз оно выпало
- 7. Вероятность - отношение числа благоприятствующих исходов, к
- 8. Достоверным называют событие, которое в результате испытание
- 9. Случайные события называются несовместными если появление одного исключает
- 10. Противоположными называют события такие, что наступление события
- 11. Для каждого из описанных событий определите, каким
- 12. Охарактеризуйте событие о котором идет речь, как
- 13. Укажите, какие из описанных пар событий являются
- 14. Совместны ли следующие события:А - у случайным
- 15. Перечислить все элементарные равновозможные события, которые могут
- 16. Назовите события, противоположные указанному:при бросании монеты выпала
- 17. В ящике находятся 2 белых и 3
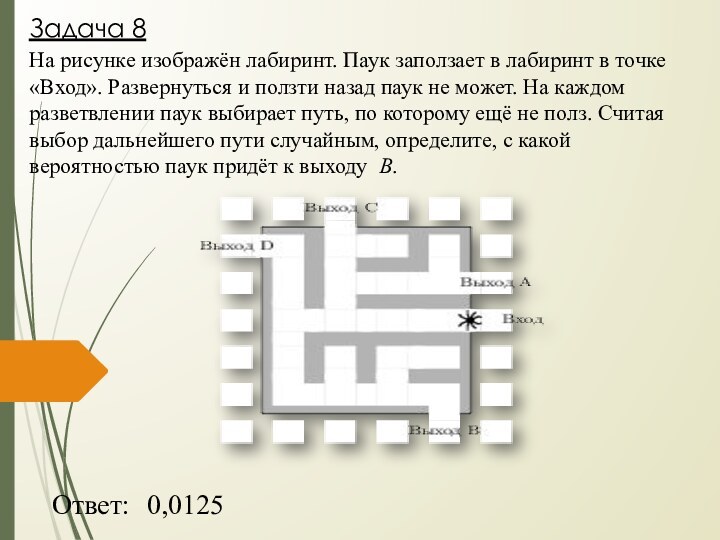
- 18. На рисунке изображён лабиринт. Паук заползает в
- 19. Механические часы с двенадцатичасовым циферблатом в какой-то
- 20. В кармане у Ромы было четыре конфеты —
- 21. По отзывам покупателей Василий Васильевич оценил
- 22. Перед началом волейбольного матча капитаны команд тянут
- 23. В Волшебной стране бывает два типа погоды:
- 24. При изготовлении подшипников диаметром 68 мм вероятность
- 25. В среднем из 1000 садовых насосов, поступивших
- 26. Фабрика выпускает сумки. В среднем на 100
- 27. В классе 33 учащихся, среди них два
- 28. В чемпионате мира участвуют 16 команд. С
- 29. Если гроссмейстер А. играет белыми, то он
- 30. Чтобы пройти в следующий круг соревнований, футбольной
- 31. В некотором городе из 3000 появившихся на
- 32. При артиллерийской стрельбе автоматическая система делает выстрел
- 33. Ковбой Джон попадает в муху на стене
- 34. Агрофирма закупает куриные яйца в двух домашних
- 35. Помещение освещается фонарём с тремя лампами. Вероятность
- 36. Вероятность того, что новый тостер прослужит больше
- 37. На фабрике керамической посуды 10% произведённых тарелок
- 38. Случайным образом выбрали трехзначное число. Какова вероятность
- 39. Бросают два кубика. С какой вероятностью выпадет хотя бы одна шестерка?Ответ:0,306Задача 31
- 40. Всем пациентам с подозрением на гепатит делают
- 41. Чтобы поступить в институт на специальность «Лингвистика»,
- 42. Чтобы открыть сейф, надо набрать в определенной
- 43. На бильярдном столе – шары от №1
- 44. Скачать презентацию
- 45. Похожие презентации










































Слайд 3 Исходом эксперимента называют значение наблюдаемого признака, непосредственно полученное
по окончании эксперимента. Каждый раз эксперимент заканчивается одним и
только одним исходом.Событием, наблюдаемым в экспериментe, называют появление исхода, обладающего заранее указанным свойством.
В конкретном эксперименте может появляться не любые события, а только такие, которые могут быть определены через свойства исходов этого эксперимента.
Слайд 4 События бывают детерминированные (солнце встает), и случайные те,
которые происходят не при каждом проведении опыта, одни случаются
чаще другие реже.Слайд 5 Под испытанием (опытом) в теории вероятностей принято понимать наблюдение какого-либо
явления при соблюдении определенного комплекса условий, который должен каждый
раз строго выполняться при повторении данного испытания. Если то же самое явление наблюдается при другом комплексе условий, то это уже другое испытание.Слайд 6 Частота события – сколько раз оно выпало в
ходе испытаний.
Относительная частота – это отношение числа испытаний в
которых событие наступило к общему числу испытаний.Слайд 7 Вероятность - отношение числа благоприятствующих исходов, к общему
числу равновозможных исходов (классическое).
Вероятность - предел относительной частоты при
неограниченном числе испытания (статистическое).Вероятность - отношение длин, площадей или объемом двух областей: общей, в которой лежат все возможные исходы и благоприятствующей, в которой лежат интересующие нас исходы
Слайд 8 Достоверным называют событие, которое в результате испытание должно
произойти.
Невозможным называют событие которое в результате испытания произойти не
может.События называются равновозможными если в результате испытания не одно из них не является объективно более возможным.
Слайд 9 Случайные события называются несовместными если появление одного исключает появление
другого. В противном случае они называются совместными.
Теорема сложения вероятностей.
Вероятность объединения произвольных событий равна сумме их вероятностей за вычетом вероятности произведения событий: Р(A+B)=Р(А)+Р(В)- Р(AB)
Слайд 10 Противоположными называют события такие, что наступление события А
означает не наступление В и наоборот.
Независимыми называются такие события,
что наступление одного из них не зависит от наступления другого.Если событие С означает совместное наступление двух независимых событий А и В, то вероятность С равна произведению вероятностей А и В.
Р(С)=Р(А)*Р(В)
Слайд 11 Для каждого из описанных событий определите, каким оно
является: невозможным, достоверным или случайным.
Из списка журнала VIII класса
(в котором есть девочки и мальчики) случайным образом выбран ученик:это мальчик;
выбранному ученику 14 лет;
выбранному ученику 14 месяцев;
этому ученику больше 2-х лет.
Задача 1
Слайд 12 Охарактеризуйте событие о котором идет речь, как достоверное,
невозможное или случайно. Даны два интервала (0;1) и (5;10).
Из первого интервала взяли число а из второго с. Оказалось что:число а меньше числа с;
число а больше числа с;
число а+с принадлежит интервалу (5;10);
число а+с не принадлежит интервалу (5;10).
Задача 2
Слайд 13 Укажите, какие из описанных пар событий являются совместными,
а какие несовместными. Из набора домино вынута одна костяшка,
на ней:одно число меньше 6, другое не больше 6;
одно число 2, сумма обоих равна 9;
оба числа больше 3, сумма чисел равна 7.
Задача 3
Слайд 14
Совместны ли следующие события:
А - у случайным образом
составленного квадратного уравнения есть действительные корни, В – дискриминант
уравнения отрицателен;А - у случайным образом составленного квадратного уравнения нет действительных корней, В – дискриминант уравнения неположителен;
Случайным образом выбранная функцияy=f(x) всюду монотонно возрастает, В- f(99)>f(100).
Задача 4
Слайд 15 Перечислить все элементарные равновозможные события, которые могут произойти
в результате:
подбрасывания 1 монеты;
подбрасывания игрального кубика;
подбрасывания тетраэдра с гранями,
занумерованными числами 1, 2, 3, 4;раскручивание стрелки рулетки, поверхность которой разделена на 5 одинаковых секторов, обозначенных буквами А, В, С, D и Е.
Задача 5
Слайд 16
Назовите события, противоположные указанному:
при бросании монеты выпала решка;
при
бросании игральной кости выпало 5 очков;
при бросании игральной кости
выпало четное число очков;Алеша вытащил выигрышный билет в розыгрыше лотереи;
после раскручивания стрелки рулетки, разделенной на 4 равных сектора, она остановилась на секторе 4;
из ящика, в котором лежат 2 белых и 3 черных шара, случайным образом вынут белый шар.
Задача 6
Слайд 17 В ящике находятся 2 белых и 3 черных
шара. Наугад вынимается один шар. Какова вероятность того, что
вынуты шар:белый;
черный;
зеленый;
белый или черный.
Задача 7
Слайд 18 На рисунке изображён лабиринт. Паук заползает в лабиринт
в точке «Вход». Развернуться и ползти назад паук не
может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу B.Ответ:
0,0125
Задача 8
Слайд 19 Механические часы с двенадцатичасовым циферблатом в какой-то момент
сломались и перестали ходить. Найдите вероятность того, что часовая
стрелка застыла, достигнув отметки 5, но не дойдя до отметки 8 часов.Ответ:
0, 25
Задача 9
Слайд 20 В кармане у Ромы было четыре конфеты — «Василёк»,
«Красная шапочка», «Белочка» и «Ласточка», а так же ключи
от квартиры. Вынимая ключи, Рома случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Красная шапочка».Ответ:
0,25
Задача 10
Слайд 21 По отзывам покупателей Василий Васильевич оценил надёжность
двух интернет-магазинов. Вероятность того, что нужный товар доставят из
магазина А, равна 0,93. Вероятность того, что этот товар доставят из магазина Б, равна 0,94. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.Ответ:
0,0042
Задача 11
Слайд 22 Перед началом волейбольного матча капитаны команд тянут честный
жребий, чтобы определить, какая из команд начнёт игру с
мячом. Команда «Стартер» по очереди играет с командами «Протор», «Ротор» и «Мотор». Найдите вероятность того, что «Стартер» будет начинать только вторую и последнюю игры.Ответ:
0,125
Задача 12
Слайд 23 В Волшебной стране бывает два типа погоды: хорошая
и отличная, причём погода, установившись утром, держится неизменной весь
день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. 6 сентября погода в Волшебной стране хорошая. Найдите вероятность того, что 9 сентября в Волшебной стране будет отличная погода.Ответ:
0,468
Задача 13
Слайд 24 При изготовлении подшипников диаметром 68 мм вероятность того,
что диаметр будет отличаться от заданного меньше чем на
0,01 мм, равна 0,968. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 67,99 мм или больше чем 68,01 мм.Ответ:
0,99
Задача 14
Слайд 25 В среднем из 1000 садовых насосов, поступивших в
продажу, 5 подтекают. Найдите вероятность того, что один случайно
выбранный для контроля насос не подтекает.Ответ:
0,995
Задача 15
Слайд 26 Фабрика выпускает сумки. В среднем на 100 качественных
сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность
того, что купленная сумка окажется качественной. Результат округлите до сотых.Ответ:
0,93
Задача 17
Слайд 27 В классе 33 учащихся, среди них два друга —
Андрей и Михаил. Класс случайным образом разбивают на 3
равные группы. Найдите вероятность того, что Андрей и Михаил окажутся в одной группе.Ответ:
0,3125
Задача 18
Слайд 28 В чемпионате мира участвуют 16 команд. С помощью
жребия их нужно разделить на четыре группы по четыре
команды в каждой. В ящике вперемешку лежат карточки с номерами групп:1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Ответ:
0,25
Задача 19
Слайд 29 Если гроссмейстер А. играет белыми, то он выигрывает
у гроссмейстера Б. с вероятностью 0,52. Если А. играет
черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.Ответ: 0,156.
Задача 20
Слайд 30 Чтобы пройти в следующий круг соревнований, футбольной команде
нужно набрать хотя бы 8 очков в двух играх.
Если команда выигрывает, она получает 5 очков, в случае ничьей — 3 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.Ответ:
0,28
Задача 21
Слайд 31 В некотором городе из 3000 появившихся на свет
младенцев 1560 мальчиков. Найдите частоту (относительную) рождения девочек в
этом городе. Результат округлите до тысячных.Ответ:
1440(0,48)
Задача 22
Слайд 32 При артиллерийской стрельбе автоматическая система делает выстрел по
цели. Если цель не уничтожена, то система делает повторный
выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?Ответ:
5
Задача 23
Слайд 33 Ковбой Джон попадает в муху на стене с
вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон
стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.Ответ:
0,68
Задача 24
Слайд 34 Агрофирма закупает куриные яйца в двух домашних хозяйствах.
40% яиц из первого хозяйства — яйца высшей категории, а
из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.Ответ:
0, 75
Задача 25
Слайд 35 Помещение освещается фонарём с тремя лампами. Вероятность перегорания
одной лампы в течение года равна 0,21. Найдите вероятность
того, что в течение года хотя бы одна лампа не перегорит.Ответ:
0,990739
Задача 27
Слайд 36 Вероятность того, что новый тостер прослужит больше года,
равна 0,94. Вероятность того, что он прослужит больше двух
лет, равна 0,8. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.Ответ:
0,14
Задача 28
Слайд 37 На фабрике керамической посуды 10% произведённых тарелок имеют
дефект. При контроле качества продукции выявляется 80% дефектных тарелок.
Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.Ответ: 0,98
Задача 29
Слайд 38 Случайным образом выбрали трехзначное число. Какова вероятность того,
то остаток от деления этого числа на 8 равен
5?Ответ:0,13
Задача 30
Слайд 39 Бросают два кубика. С какой вероятностью выпадет хотя
бы одна шестерка?
Ответ:0,306
Задача 31
Слайд 40 Всем пациентам с подозрением на гепатит делают анализ
крови. Если анализ выявляет гепатит, то результат анализа называется положительным.
У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.Ответ: 0,0545
Задача 32
Слайд 41 Чтобы поступить в институт на специальность «Лингвистика», абитуриент
должен набрать на ЕГЭ не менее 70 баллов по каждому
из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Ответ: 0,408
Задача 33
Слайд 42 Чтобы открыть сейф, надо набрать в определенной последовательности
5 цифр (без из повторения): 1, 2, 3, 4,
5. Какова вероятность того, что если набирать цифры в произвольном порядке, то сейф откроется. Результат округлите до сотых.Ответ:0,008
Задача 34
Слайд 43 На бильярдном столе – шары от №1 до
№15 и еще шар «крест». Бить можно любым шаром
по любому. Найдите вероятность того, что при случайном выборе:ударят шаром №7 по какому то другому шару;
ударят по шару №7 шаром с меньшим номером;
ударят «крестом» по шару №7;
ударят «крестом» по шару с двузначным номером;
Задача 35





























