Слайд 2
Оформление титульного листа
Слайд 6
Всего 5 заданий
ЗАДАНИЕ №3.
Повторные независимые испытания. Формула
Бернулли. Формула Пуассона. Формула Муавра-Лапласа.
ЗАДАНИЕ №4.
Закон распределения
вероятностей случайных дискретных величин. Числовые характеристики дискретных случайных величин. Функция распределения вероятностей случайной величины.
ЗАДАНИЕ №5
Статистическое распределение. Геометрическое изображение. Выборочные характеристики статистического распределения.
Слайд 7
Основные понятия
Событием называется всякий факт, который может произойти
или не произойти в результате опыта.
При этом тот
или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда. В отношении друг друга события также имеют особенности, т.е. в одном случае событие А может произойти совместно с событием В, в другом – нет.
Слайд 8
Основные понятия
События называются несовместными, если появление одного из
них исключает появление других.
Классическим примером несовместных событий является
результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).
Полной группой событий называется совокупность всех возможных результатов опыта.
Слайд 9
Основные понятия
Достоверным событием называется событие, которое наверняка произойдет
в результате опыта. Событие называется невозможным, если оно никогда
не произойдет в результате опыта.
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие.
Появление красного и появление зеленого шаров образуют полную группу событий.
Слайд 10
Основные понятия
События называются равновозможными, если нет оснований считать,
что одно из них появится в результате опыта с
большей вероятностью.
В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров. Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного
Слайд 11
Основные понятия
Вероятностью события А называется математическая оценка возможности
появления этого события в результате опыта. Вероятность события А
равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий
Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.
Очевидно, что вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей
Слайд 12
Основные понятия
Относительной частотой события А называется отношение числа
опытов, в результате которых произошло событие А к общему
числу опытов. Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.
Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна
При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события
Слайд 13
Операции над событиями
События А и В называются равными,
если осуществление события А влечет за собой осуществление события
В и наоборот.
Объединением или суммой событий Аk называется событие A, которое означает появление хотя бы одного из событий Аk
Пересечением или произведением событий Ak называется событие А, которое заключается в осуществлении всех событий Ak.
Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В
Дополнительным к событию А называется событие означающее, что событие А не происходит.
Слайд 14
Операции над событиями
Элементарными исходами опыта называются такие результаты
опыта, которые взаимно исключают друг друга и в результате
опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие. Совокупность всех элементарных исходов опыта называется пространством элементарных событий.
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
Слайд 15
Операции над событиями
Противоположными называются два несовместных события, образующие
полную группу.
Теорема. Вероятность появления хотя бы одного из двух
совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Слайд 16
Операции над событиями
Событие А называется независимым от события
В, вероятность события А не зависит от того, произошло
событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.
Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.
Слайд 25
Формула полной вероятности
Теорема. Вероятность события А, которое может
произойти вместе с одним из событий Н1,Н2, … Нn
равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.
Слайд 41
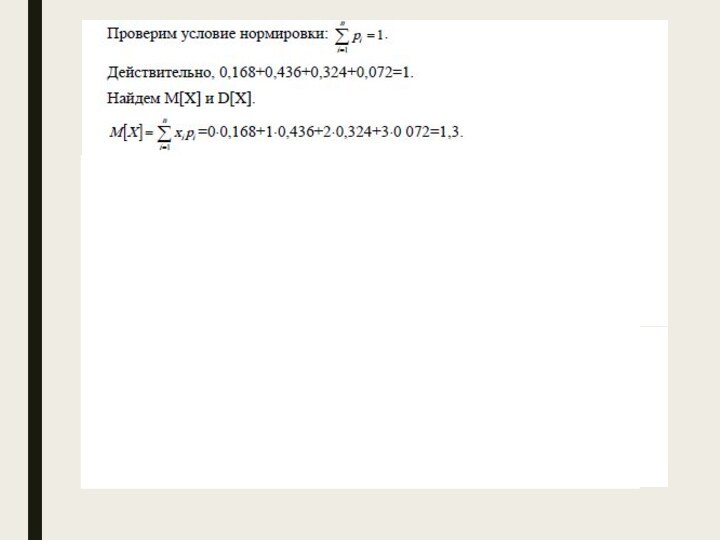
Числовые характеристики случайной величины
Слайд 42
Числовые характеристики случайной величины