- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора
Содержание
- 2. S1S2S3S=S1+S2+S3Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников
- 3. ∆ABC=∆MNK, Равные многоугольники имеют равные площади.значит SABC=SMNKАВСMNK
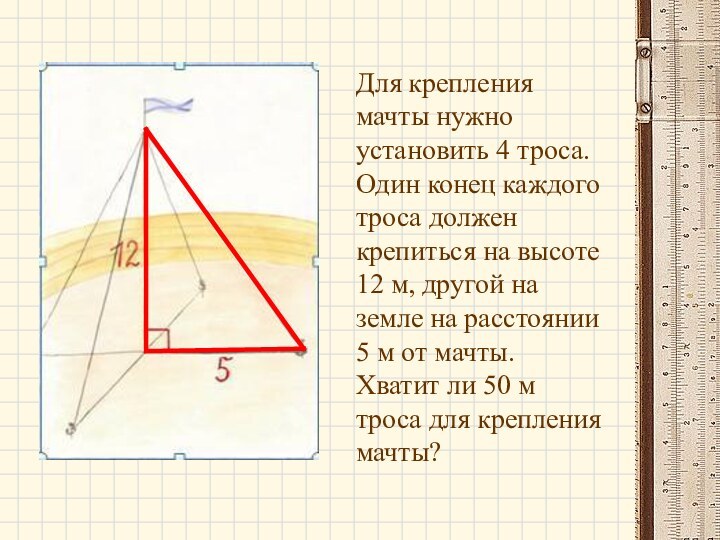
- 4. Для крепления мачты нужно установить 4 троса.
- 5. Практическая работа15
- 6. Теорема Пифагора
- 7. Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетовabc
- 8. «Умение решать задачи – такое же
- 9. №1. Найдите гипотенузу с прямоугольного треугольника по данным катетам: a= 6 см, b=8 см.abc - ?
- 10. №2. В прямоугольном треугольнике известен катет a=9 см и гипотенуза c=41 см, найдите второй катет.acb-?
- 11. Выяснить, что нужно найти, и что нам для этого дано;Применить нужную формулу;Рассмотреть прямоугольный треугольник;АЛГОРИТМ
- 12. Соотнесите треугольник, и верную запись теоремы Пифагораaaabbbccca2=b2+c2b2=a2+c2c2=a2+b2
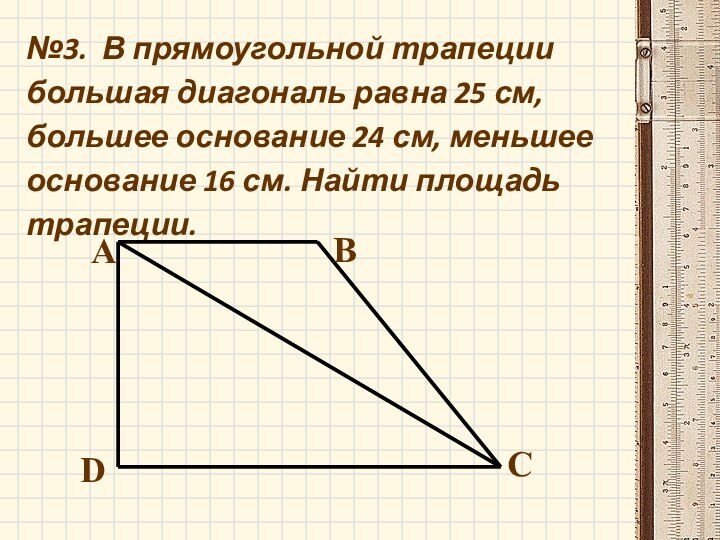
- 13. АВСD
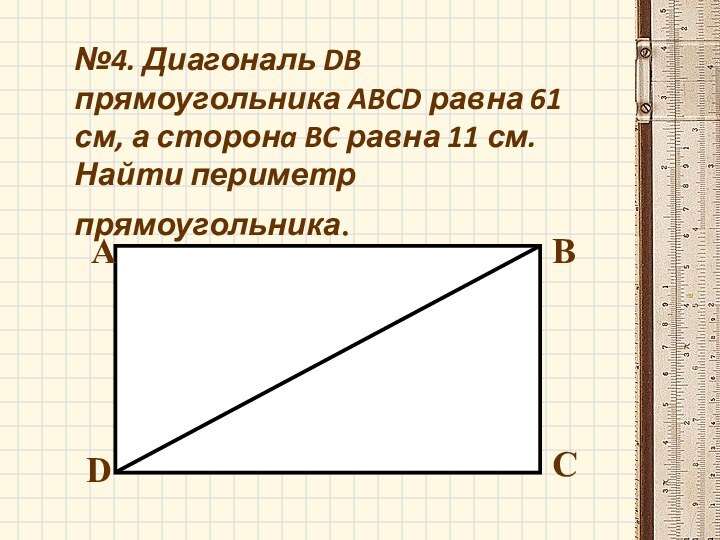
- 14. №4. Диагональ DB прямоугольника ABCD равна 61
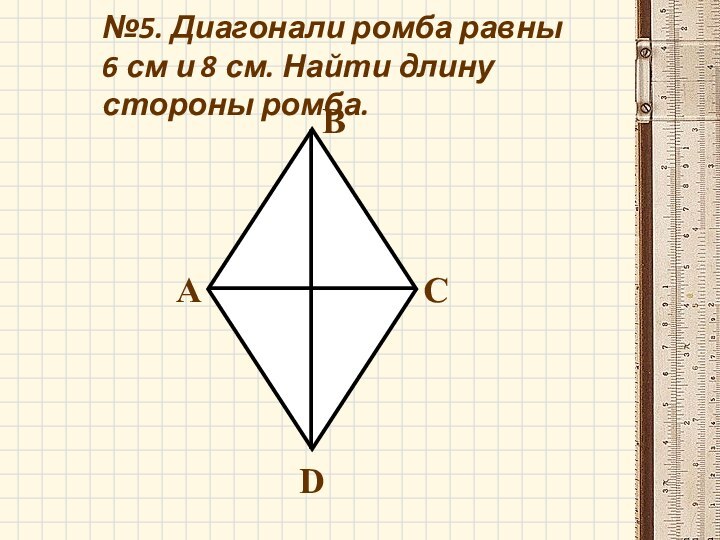
- 15. №5. Диагонали ромба равны 6 см и 8 см. Найти длину стороны ромба.АВСD
- 16. «Правило верёвки»
- 17. Над озером тихим, С полфута размером, высился
- 18. фута2 футах футовх +футаАВСD
- 19. Домашнее задание:Выучить формулировку и доказательство теоремы Пифагора
- 21. Скачать презентацию
- 22. Похожие презентации
S1S2S3S=S1+S2+S3Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

















Слайд 2
S1
S2
S3
S=S1+S2+S3
Если многоугольник составлен из нескольких многоугольников, то его
площадь равна сумме площадей этих многоугольников
Слайд 4 Для крепления мачты нужно установить 4 троса. Один
конец каждого троса должен крепиться на высоте 12 м,
другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?Слайд 8 «Умение решать задачи – такое же практическое искусство.
Ему можно научиться только путем подражания или упражнения»
(Д.
Пойа)
Слайд 9
№1. Найдите гипотенузу с прямоугольного треугольника по данным
катетам: a= 6 см, b=8 см.
a
b
c - ?
Слайд 10 №2. В прямоугольном треугольнике известен катет a=9 см
и гипотенуза c=41 см, найдите второй катет.
a
c
b-?
Слайд 11 Выяснить, что нужно найти, и что нам для
этого дано;
Применить нужную формулу;
Рассмотреть прямоугольный треугольник;
АЛГОРИТМ
Слайд 14
№4. Диагональ DB прямоугольника ABCD равна 61 см,
а сторонa BC равна 11 см. Найти периметр прямоугольника.
А
В
С
D
Слайд 17
Над озером тихим,
С полфута размером, высился лотоса
цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону.
НетБоле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Задача древних индусов
Слайд 19
Домашнее задание:
Выучить формулировку и доказательство теоремы Пифагора (Глава
6 параграф 3) (можно предложить другое, отличное от разобранного
нами);Решить задачу, которую мы сформулировали в начале урока, хватит ли нам верёвки для закрепления мачты;
Довести до ответа задачу древних индусов;
Необязательное задание:
Задача из китайской «Математики в девяти книгах»;
Задача из учебника «Арифметика» Леонтия Магницкого.