Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Урок-презентация по теме Прикладные задачи геометрии.

Содержание

Тема факультатива по математики:Прикладные задачи геометрии.Тема :Прикладные задачи геометрии.Выполнила: учитель математики МКОУ В(С)Ш №36Кузина Е.Г.
Тема факультатива по математики:Прикладные задачи геометрии.Тема :Прикладные задачи геометрии.Выполнила: учитель математики МКОУ В(С)Ш №36Кузина Е.Г. Прикладная (практическая) задача – это задача, поставленная вне математики и решаемая математическими средствами. Цель работы: Рассмотреть различные задачи прикладного характера, изучить  методы их решения, и применение на практике. Задачи:изучение элементарных методов решения прикладных задач геометрииотработка навыков их решения и применения на практикеподготовка к ГИА Задание № 506634       Два садовода, име­ю­щие пря­мо­уголь­ные участ­ки раз­ме­ра­ми 20 м на 30 м Решение.Площадь каждого из участков равна 20 · 30 = 600 кв. м, Задание № 506574Дач­ный уча­сток имеет форму прямоугольника, сто­ро­ны ко­то­ро­го равны 40 м Решение.Площадь прямоугольника равна произведению его длины на ширину, поэтому площадь участка равна Задача. Рулон обоев имеет длину 10 м и ширину 50 см. Сколько Решение:Рулон обоев:10 м – длина, 50 см – ширина 50 см-0,5м.Стена:6,5 м Практическая работа.-Вам необходимо рассчитать, сколько потребуется рулонов обоев размером 66,5см на 4см Дополнительный материал.Выясните знания каких тем вам будут необходимы при решении следующих задач. И решите их. Задание № 506863Ко­ле­со имеет 25 спиц. Най­ди­те ве­ли­чи­ну угла (в градусах), ко­то­рый об­ра­зу­ют две со­сед­ние спицы. Решение.Спицы делят колесо на двадцать пять равных секторов, а значит, делят полный Задание № 511458Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 13:00? Решение.Угол между двумя часовыми делениями на циферблате равен 360°/12 = 30°. В Задание № 506741Детская горка укреп­ле­на вер­ти­каль­ным столбом, рас­по­ло­жен­ным по­се­ре­ди­не спуска. Най­ди­те вы­со­ту Решение.Данная конструкция представляет собой треугольник, в котором столб является средней линией. Длина Задание № 507933Перила лест­ни­цы дач­но­го дома для надёжности укреп­ле­ны по­се­ре­ди­не вер­ти­каль­ным столбом. 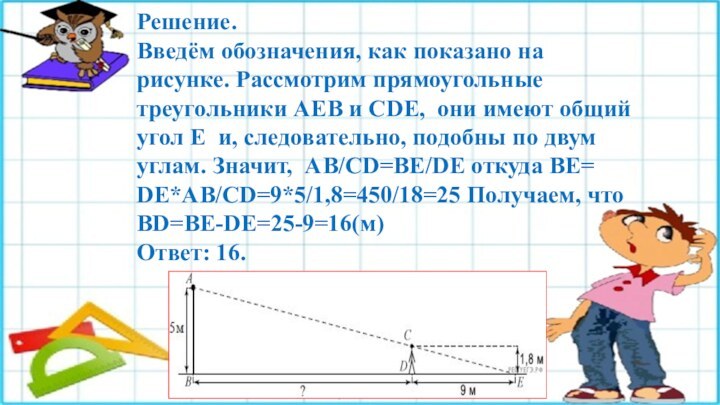Решение.Заметим, что данная конструкция представляет собой трапецию, а столб — средняя линия Задание № 512360На каком рас­сто­я­нии (в метрах) от фо­на­ря стоит че­ло­век ростом Решение.Введём обозначения, как показано на рисунке. Рассмотрим прямоугольные треугольники АЕВ и СDЕ, Задание № 514527От столба к дому натянут провод длиной 15 м, который Решение.Пусть длина искомой стороны равна Х. Проведём отрезок, параллельный горизонтальной прямой, как Рефлексия сегодня я узнал...было трудно…я понял, что…я научился…я смог…было интересно узнать, что…меня удивило…мне захотелось…
Слайды презентации

Слайд 2 Тема факультатива по математики:
Прикладные задачи геометрии.
Тема :
Прикладные задачи

Тема факультатива по математики:Прикладные задачи геометрии.Тема :Прикладные задачи геометрии.Выполнила: учитель математики МКОУ В(С)Ш №36Кузина Е.Г.

геометрии.
Выполнила: учитель математики МКОУ В(С)Ш №36
Кузина Е.Г.

Слайд 3 Прикладная (практическая) задача – это задача, поставленная вне

Прикладная (практическая) задача – это задача, поставленная вне математики и решаемая математическими средствами.

математики и решаемая математическими средствами.

Слайд 4 Цель работы:
Рассмотреть различные задачи прикладного характера, изучить

Цель работы: Рассмотреть различные задачи прикладного характера, изучить  методы их решения, и применение на практике.

 методы их решения, и применение на практике.

Слайд 5 Задачи:
изучение элементарных методов решения прикладных задач геометрии
отработка навыков

Задачи:изучение элементарных методов решения прикладных задач геометрииотработка навыков их решения и применения на практикеподготовка к ГИА

их решения и применения на практике
подготовка к ГИА

Слайд 6 Задание № 506634
      Два садовода, име­ю­щие пря­мо­уголь­ные участ­ки раз­ме­ра­ми 20

Задание № 506634       Два садовода, име­ю­щие пря­мо­уголь­ные участ­ки раз­ме­ра­ми 20 м на 30

м на 30 м с общей границей, до­го­во­ри­лись и

сде­ла­ли общий пря­мо­уголь­ный пруд раз­ме­ром 10 м на 14 м (см. чертёж), причём гра­ни­ца участ­ков про­хо­дит точно через центр. Ка­ко­ва пло­щадь (в квад­ратных метрах) оставшейся части участка каждого садовода?

Слайд 7 Решение.
Площадь каждого из участков равна 20 · 30

Решение.Площадь каждого из участков равна 20 · 30 = 600 кв.

= 600 кв. м, а площадь пруда равна 10

· 14 = 140 кв. м. На каждом участке находится половина пруда, занимая 70 кв. м. Поэтому площадь оставшейся части каждого из участков равна 600 − 70 = 530 кв. м.

Ответ: 530.

Слайд 8 Задание № 506574
Дач­ный уча­сток имеет форму прямоугольника, сто­ро­ны

Задание № 506574Дач­ный уча­сток имеет форму прямоугольника, сто­ро­ны ко­то­ро­го равны 40

ко­то­ро­го равны 40 м и 30 м. Раз­ме­ры дома,

рас­по­ло­жен­но­го на участ­ке и также име­ю­ще­го форму прямоугольника, — 9 м × 6 м. Най­ди­те пло­щадь остав­шей­ся части участка. Ответ дайте в квад­рат­ных метрах.

Слайд 9 Решение.
Площадь прямоугольника равна произведению его длины на ширину,

Решение.Площадь прямоугольника равна произведению его длины на ширину, поэтому площадь участка

поэтому площадь участка равна 40 · 30=1200 кв.м. Площадь

дома равна 6 · 9 = 54 кв.м. Тем самым, площадь участка, незанятого домом равна 1200 − 54 = 1146 кв.м.

Ответ: 1146

Слайд 10 Задача. Рулон обоев имеет длину 10 м и ширину

Задача. Рулон обоев имеет длину 10 м и ширину 50 см.

50 см. Сколько нужно таких рулонов обоев, чтобы оклеить

стену длиной 5 м и шириной 2,5 м ?

Слайд 11 Решение:
Рулон обоев:
10 м – длина,
50 см –

Решение:Рулон обоев:10 м – длина, 50 см – ширина 50 см-0,5м.Стена:6,5

ширина 50 см-0,5м.
Стена:
6,5 м длина,
2,5 м – ширина
Обои -?
S=a*b

площадь
0,5*10=5 м² площадь рулона площадь обоев
6.5*2,5=16,25м²  площадь стены
16,25:5=3,25 рулонов обоев требуется чтобы оклеить комнату.
Ответ 4 рулона

Слайд 12 Практическая работа.
-Вам необходимо рассчитать, сколько потребуется рулонов обоев

Практическая работа.-Вам необходимо рассчитать, сколько потребуется рулонов обоев размером 66,5см на

размером 66,5см на 4см для оклеивания стены, если размеры

стены 42 см на 30 см.
-Рассчитать при этом площадь оклеиваемой поверхности, площадь рулона обоев, количество обоев.
-Приобрести их и оклеить ими данную стену.
-Все материалы и инструмент можно получить у учителя.

Слайд 13 Дополнительный материал.

Выясните знания каких тем вам будут необходимы

Дополнительный материал.Выясните знания каких тем вам будут необходимы при решении следующих задач. И решите их.

при решении следующих задач. И решите их.

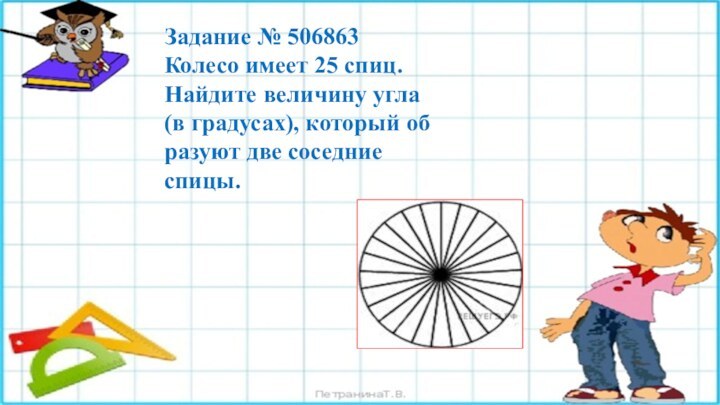
Слайд 14 Задание № 506863
Ко­ле­со имеет 25 спиц. Най­ди­те ве­ли­чи­ну

Задание № 506863Ко­ле­со имеет 25 спиц. Най­ди­те ве­ли­чи­ну угла (в градусах), ко­то­рый об­ра­зу­ют две со­сед­ние спицы.

угла (в градусах), ко­то­рый об­ра­зу­ют две со­сед­ние спицы.

Слайд 15 Решение.
Спицы делят колесо на двадцать пять равных секторов,

Решение.Спицы делят колесо на двадцать пять равных секторов, а значит, делят

а значит, делят полный угол 360° на 25 равных

углов по 14,4° каждый

Ответ: 14,4.

Слайд 16 Задание № 511458
Какой наименьший угол (в градусах) образуют

Задание № 511458Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 13:00?

минутная и часовая стрелки часов в 13:00?

Слайд 17 Решение.
Угол между двумя часовыми делениями на циферблате равен

Решение.Угол между двумя часовыми делениями на циферблате равен 360°/12 = 30°.

360°/12 = 30°. В час дня между минутной и

часовой стрелкой одно часовое деление, значит, угол (наименьший) между ними равен 30° · 1 = 30°.

Ответ: 30

Слайд 18 Задание № 506741
Детская горка укреп­ле­на вер­ти­каль­ным столбом, рас­по­ло­жен­ным

Задание № 506741Детская горка укреп­ле­на вер­ти­каль­ным столбом, рас­по­ло­жен­ным по­се­ре­ди­не спуска. Най­ди­те

по­се­ре­ди­не спуска. Най­ди­те вы­со­ту l этого столба, если вы­со­та

h горки равна 2 метрам. Ответ дайте в метрах.

Слайд 19 Решение.
Данная конструкция представляет собой треугольник, в котором столб

Решение.Данная конструкция представляет собой треугольник, в котором столб является средней линией.

является средней линией. Длина средней линии треугольника равна половине

длины стороны, которой она параллельна: l = 2/2 = 1 м.

Ответ: 1.

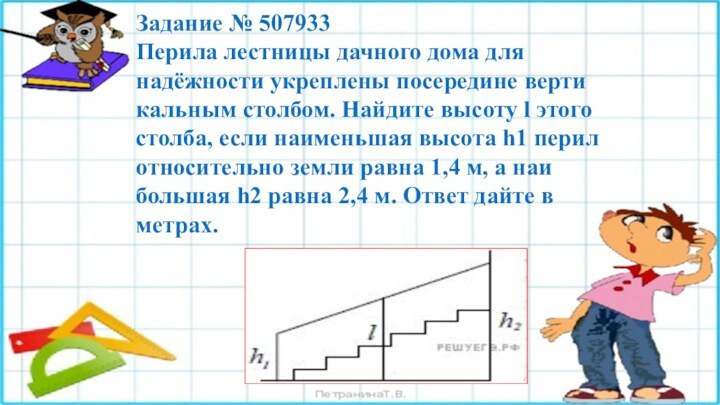
Слайд 20 Задание № 507933
Перила лест­ни­цы дач­но­го дома для надёжности

Задание № 507933Перила лест­ни­цы дач­но­го дома для надёжности укреп­ле­ны по­се­ре­ди­не вер­ти­каль­ным

укреп­ле­ны по­се­ре­ди­не вер­ти­каль­ным столбом. Най­ди­те вы­со­ту l этого столба,

если наи­мень­шая вы­со­та h1 перил от­но­си­тель­но земли равна 1,4 м, а наи­боль­шая h2 равна 2,4 м. Ответ дайте в метрах.

Слайд 21 Решение.
Заметим, что данная конструкция представляет собой трапецию, а

Решение.Заметим, что данная конструкция представляет собой трапецию, а столб — средняя

столб — средняя линия данной трапеции. Длина средней линии

трапеции равна полусумме оснований: (2,4+1,4)/2=1,9


Ответ: 1,9.

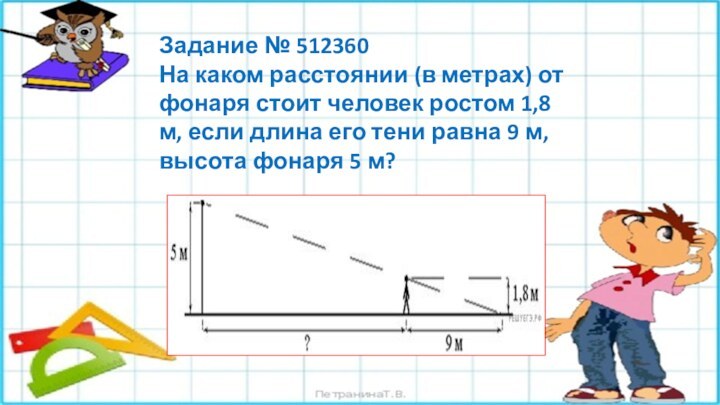
Слайд 22 Задание № 512360
На каком рас­сто­я­нии (в метрах) от

Задание № 512360На каком рас­сто­я­нии (в метрах) от фо­на­ря стоит че­ло­век

фо­на­ря стоит че­ло­век ростом 1,8 м, если длина его

тени равна 9 м, вы­со­та фонаря 5 м?

Слайд 23 Решение.
Введём обозначения, как показано на рисунке. Рассмотрим прямоугольные

Решение.Введём обозначения, как показано на рисунке. Рассмотрим прямоугольные треугольники АЕВ и

треугольники АЕВ и СDЕ, они имеют общий угол Е

и, следовательно, подобны по двум углам. Значит, АВ/СD=ВЕ/DE откуда BE= DE*AB/CD=9*5/1,8=450/18=25 Получаем, что BD=BE-DE=25-9=16(м)
Ответ: 16.

Слайд 24 Задание № 514527
От столба к дому натянут провод

Задание № 514527От столба к дому натянут провод длиной 15 м,

длиной 15 м, который закреплён на стене дома на

высоте 3 м от земли (см. рисунок). Найдите высоту столба, если расстояние от дома до столба равно 12 м. Ответ дайте в метрах.

Слайд 25 Решение.
Пусть длина искомой стороны равна Х. Проведём отрезок,

Решение.Пусть длина искомой стороны равна Х. Проведём отрезок, параллельный горизонтальной прямой,

параллельный горизонтальной прямой, как показано на рисунке, тогда Х-3

— катет получившегося прямоугольного треугольника. По теореме Пифагора: Х-3= √152 -122=√225-144=9
Следовательно, длина искомой стороны равна 12.
Ответ:12
  • Имя файла: urok-prezentatsiya-po-teme-prikladnye-zadachi-geometrii.pptx
  • Количество просмотров: 166
  • Количество скачиваний: 2
- Предыдущая Закрепление и обобщение знаний
Следующая - Технологическая карта занятия по внеурочной деятельности Виртуальное путешествие по Лондону

Похожие презентации

Технологическая карта урока по музыке в 1 классе Музыка и ты Технологическая карта урока по музыке в 1 классе Музыка и ты 180
Презентация Водяной насос. Гидравлический пресс Презентация Водяной насос. Гидравлический пресс 171
Занятие Зимние олимпийские игры Занятие Зимние олимпийские игры 105
Герои Советского Союза и России Герои Советского Союза и России 157
Разрешение педагогических ситуаций и конфликтов в работе учителя. презентация к уроку по теме Разрешение педагогических ситуаций и конфликтов в работе учителя. презентация к уроку по теме 185
Шаблон для интерактивной презентации Островки Шаблон для интерактивной презентации Островки 106
Миклухо-Маклай Николай Николаевич Миклухо-Маклай Николай Николаевич 136
Метапредметные результаты обучения Метапредметные результаты обучения 135
Шаблон презентации по инофрматике Шаблон презентации по инофрматике 115
Интеллектуальная игра Пятерочка по географии для 7-8 классов Интеллектуальная игра Пятерочка по географии для 7-8 классов 201
Презентация Путешественники и открытия в географии Презентация Путешественники и открытия в географии 124
Презентация урока математики Как найти неизвестный множитель, 3 класс Презентация урока математики Как найти неизвестный множитель, 3 класс 47
Презентация Георгиевская лента Презентация Георгиевская лента 145
В гостях к осени В гостях к осени 138
Презентация Тропические растения. Такие разные цветы, часть 2 Презентация Тропические растения. Такие разные цветы, часть 2 138
Дидактические игры и упражнения для профилактики дисграфии у детей дошкольного возраста Дидактические игры и упражнения для профилактики дисграфии у детей дошкольного возраста 118
Театрализованные игры как средство развития творческих способностей детей дошкольного возраста. Театрализованные игры как средство развития творческих способностей детей дошкольного возраста. 102
Презентация к уроку русского языка по теме Винительный падеж Презентация к уроку русского языка по теме Винительный падеж 127
Презентация Реформы Избранной Рады Презентация Реформы Избранной Рады 202
Презентация к уроку русского языка Безударные окончания глаголов, 4 класс Презентация к уроку русского языка Безударные окончания глаголов, 4 класс 120
Презентация Средневековые университеты Европы Презентация Средневековые университеты Европы 158
Презентация Средства диагностирования рулевого управления (МДК 01.02) Презентация Средства диагностирования рулевого управления (МДК 01.02) 208
Презентация к уроку Понятие о предлогах и их правописание Презентация к уроку Понятие о предлогах и их правописание 99
Презентация урока литературного чтения Саша Черный. Дневник фокса Микки. Я один. Продолжение Презентация урока литературного чтения Саша Черный. Дневник фокса Микки. Я один. Продолжение 157
Презентация Многообразие и значение кишечнополостных Презентация Многообразие и значение кишечнополостных 145
Презентация к уроку чтения по теме И. Бунин. Листопад. Слово как средство художественной выразительности. Сравнения, эпитеты. Презентация к уроку чтения по теме И. Бунин. Листопад. Слово как средство художественной выразительности. Сравнения, эпитеты. 145
Презентация Н.В. Гоголь Ночь перед Рождеством, 2 часть Презентация Н.В. Гоголь Ночь перед Рождеством, 2 часть 111
Аттестационная работа. Рабочая программа учебного курса. Основы исследовательской и проектной деятельности Аттестационная работа. Рабочая программа учебного курса. Основы исследовательской и проектной деятельности 139
Презентация Умный дом Презентация Умный дом 1424
Конспект вводного урока биологии в 6 классе специальных (коррекционных) школ VIII вида на тему: Неживая и живая природа Конспект вводного урока биологии в 6 классе специальных (коррекционных) школ VIII вида на тему: Неживая и живая природа 153