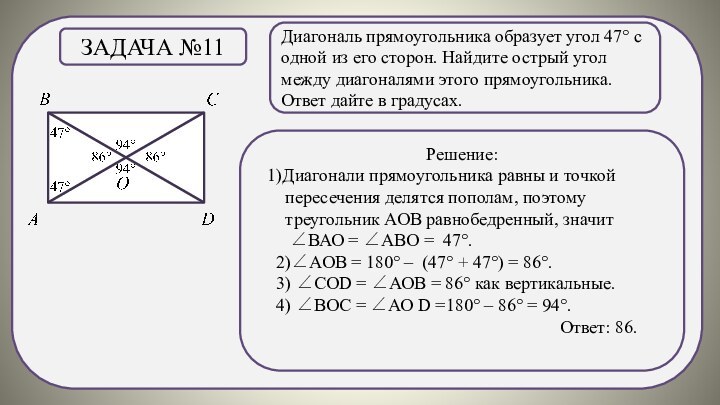
его сторон. Найдите острый угол между диагоналями этого прямоугольника.
Ответ
дайте в градусах.Задача №11
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















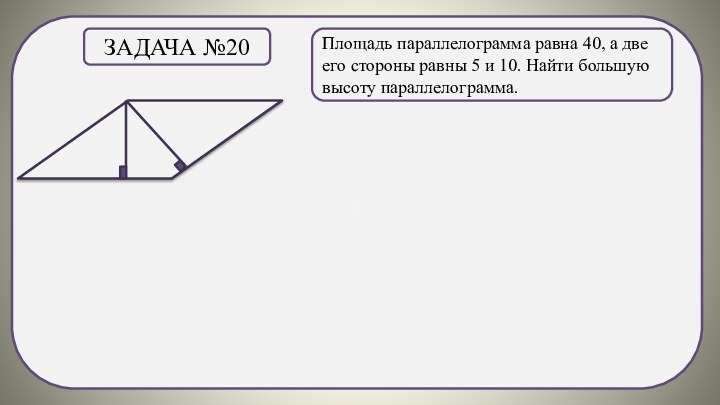
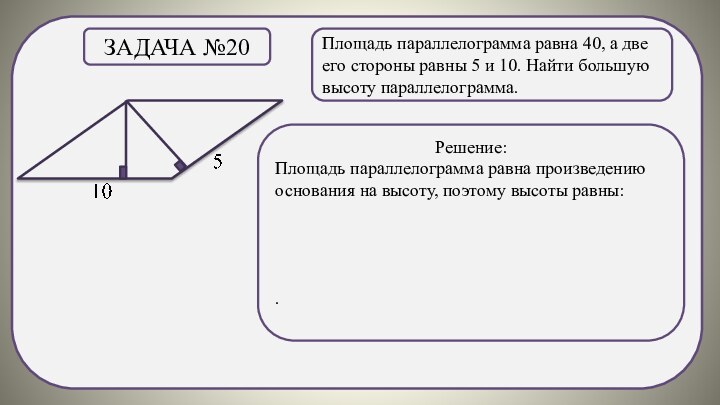
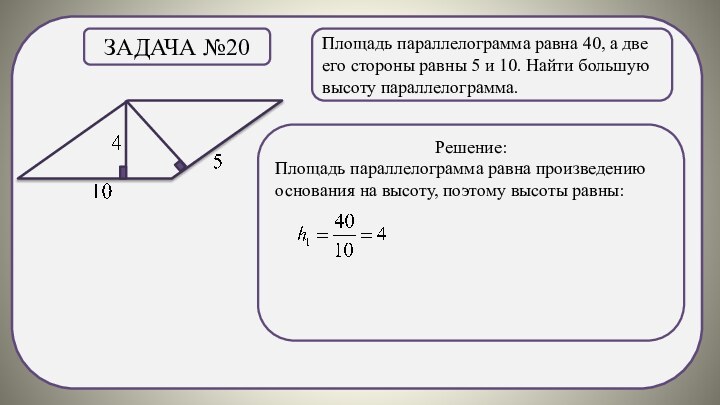
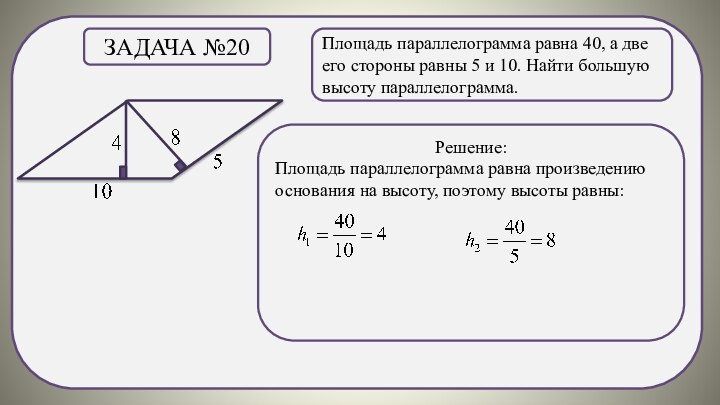
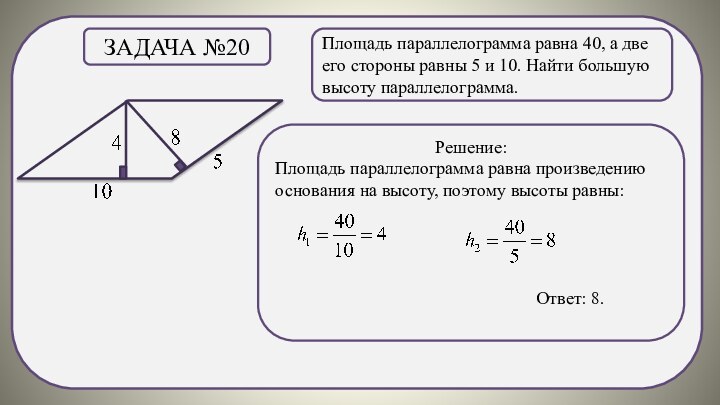


Задача №11
Задача №11
Решение:
Задача №11
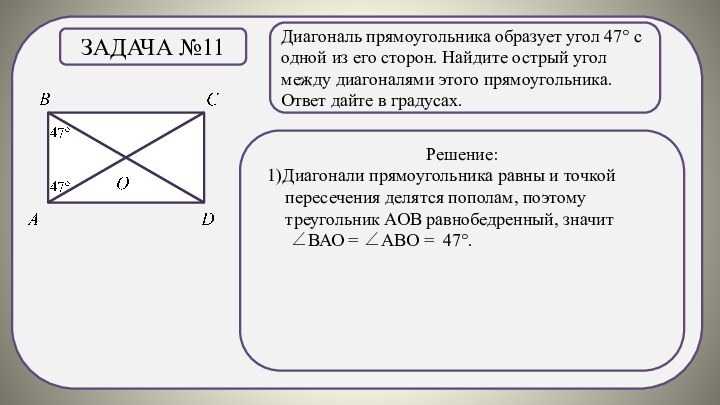
Решение:
1)Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому треугольник АОВ равнобедренный, значит
∠ВАО = ∠АВО = 47°.
Задача №11
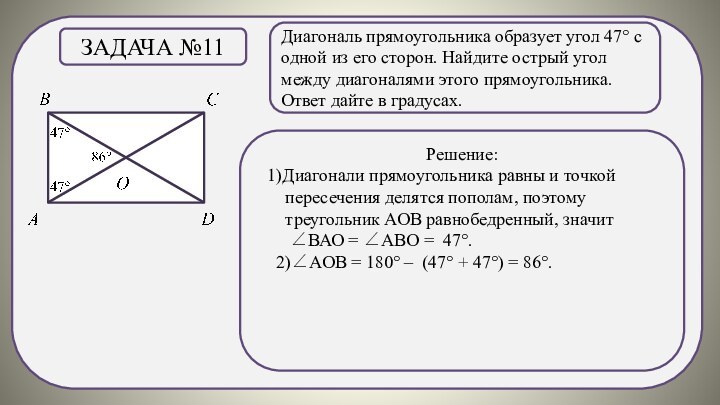
Решение:
1)Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому треугольник АОВ равнобедренный, значит
∠ВАО = ∠АВО = 47°.
2)∠АОВ = 180° – (47° + 47°) = 86°.
Задача №11
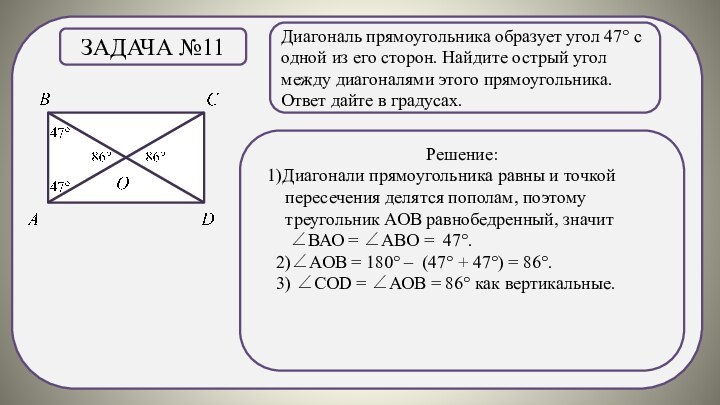
Решение:
1)Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому треугольник АОВ равнобедренный, значит
∠ВАО = ∠АВО = 47°.
2)∠АОВ = 180° – (47° + 47°) = 86°.
3) ∠СОD = ∠АОВ = 86° как вертикальные.
Задача №11
Решение:
1)Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому треугольник АОВ равнобедренный, значит
∠ВАО = ∠АВО = 47°.
2)∠АОВ = 180° – (47° + 47°) = 86°.
3) ∠СОD = ∠АОВ = 86° как вертикальные.
4) ∠ВОС = ∠АО D =180° – 86° = 94°.
Ответ: 86.
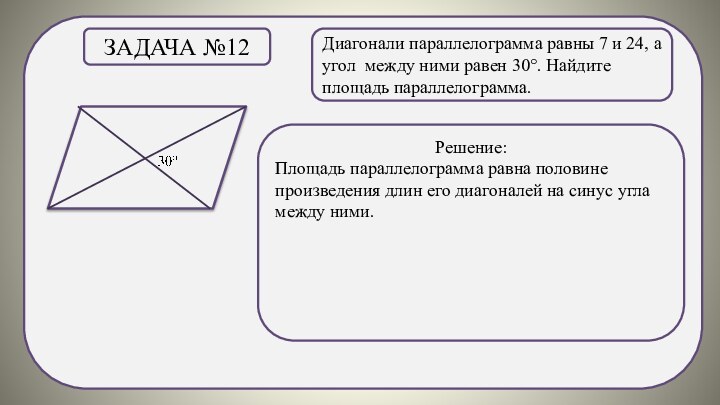
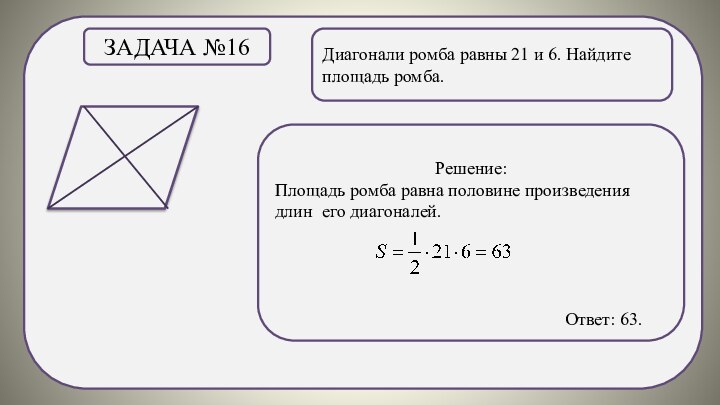
Задача №12
Задача №12
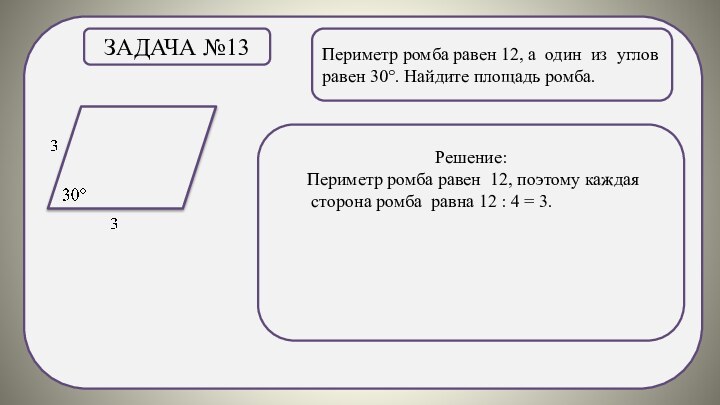
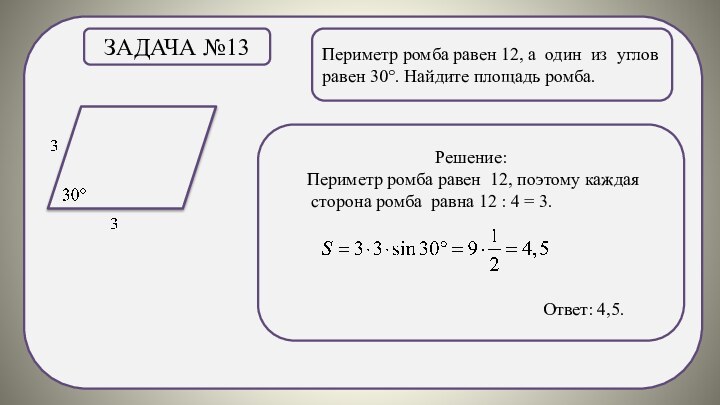
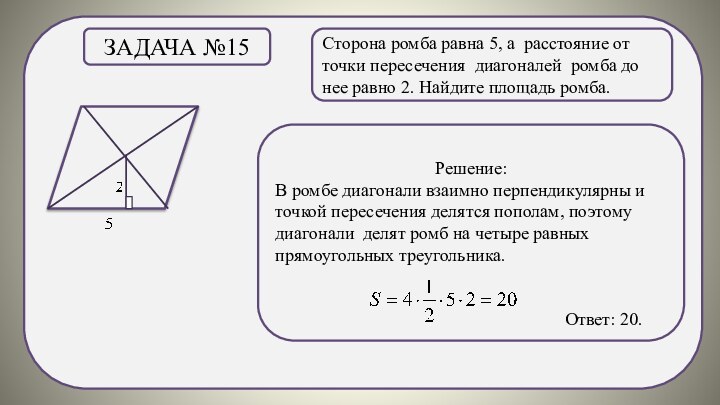
Задача №15
Задача №15
Решение:
В ромбе диагонали взаимно перпендикулярны и точкой пересечения делятся пополам, поэтому
диагонали делят ромб на четыре равных прямоугольных треугольника.
Ответ: 20.
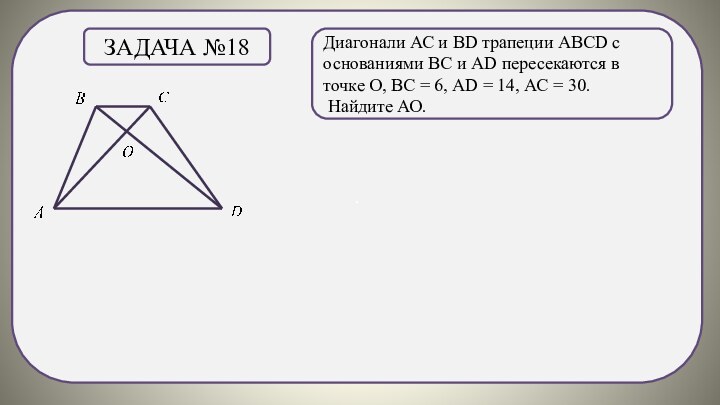
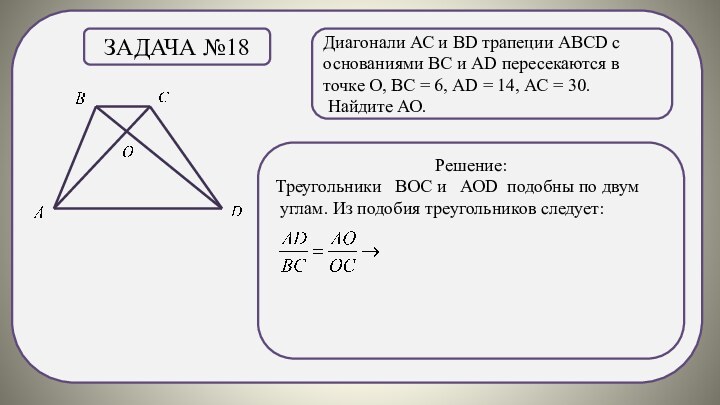
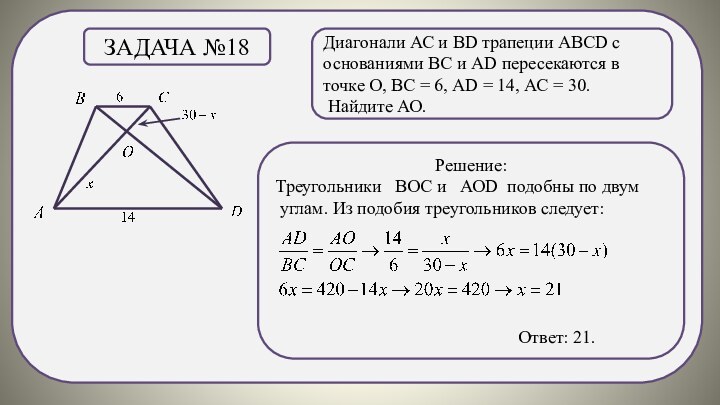
Задача №18
Задача №18
Решение:
Треугольники ВОС и АОD подобны по двум
углам. Из подобия треугольников следует:
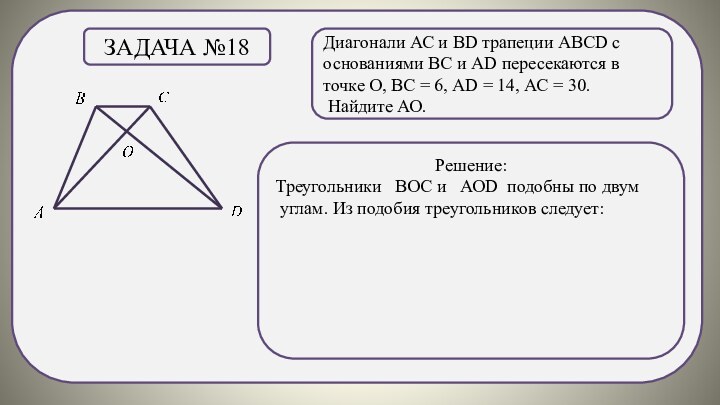
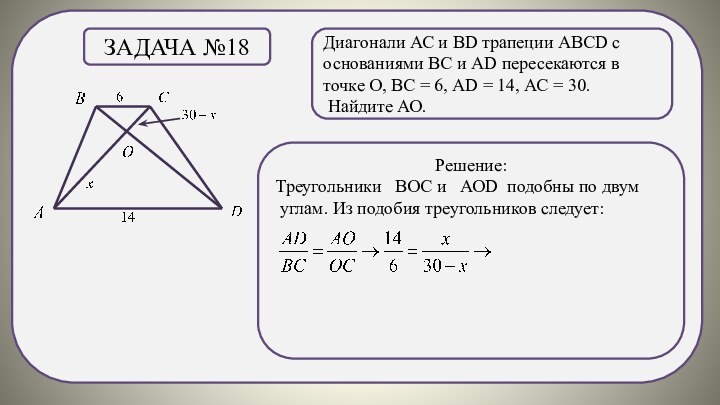
Задача №18
Решение:
Треугольники ВОС и АОD подобны по двум
углам. Из подобия треугольников следует:
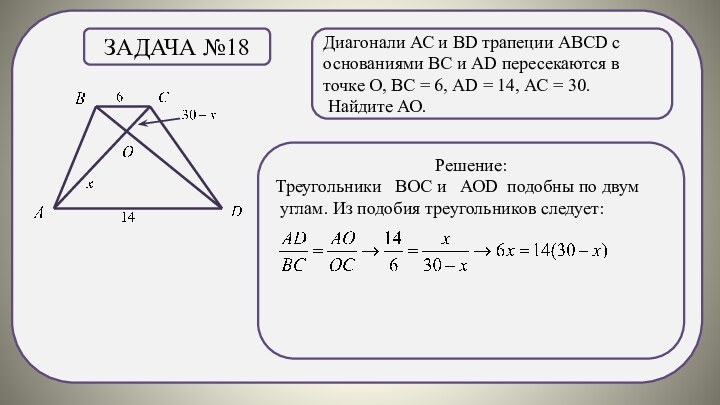
Задача №18
Решение:
Треугольники ВОС и АОD подобны по двум
углам. Из подобия треугольников следует:
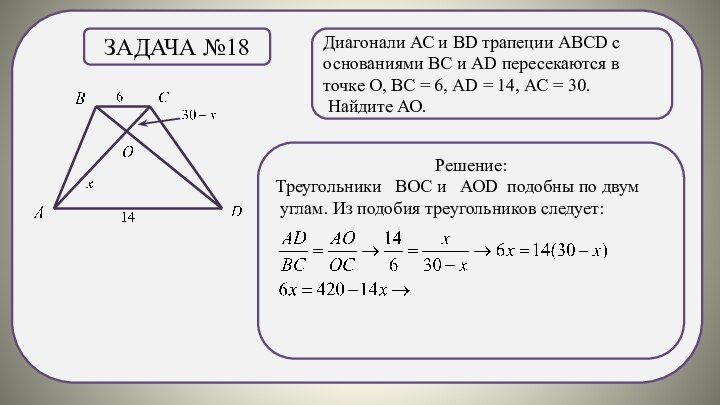
Задача №18
Решение:
Треугольники ВОС и АОD подобны по двум
углам. Из подобия треугольников следует:
Задача №18
Решение:
Треугольники ВОС и АОD подобны по двум
углам. Из подобия треугольников следует:
Задача №18
Решение:
Треугольники ВОС и АОD подобны по двум
углам. Из подобия треугольников следует:
Ответ: 21.
Задача №19
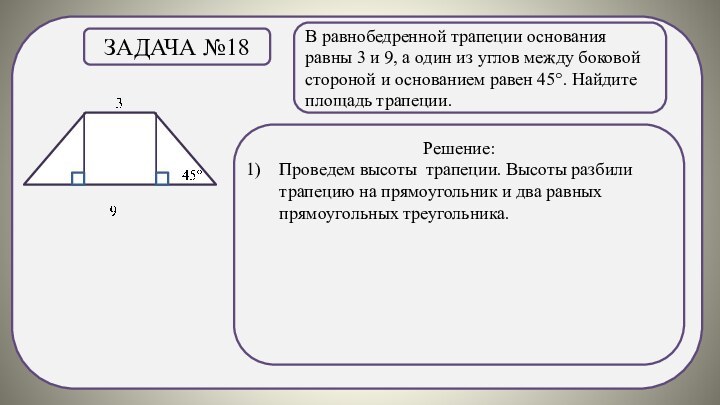
Задача №18
Решение:
Проведем высоты трапеции. Высоты разбили трапецию на прямоугольник и два равных прямоугольных треугольника.
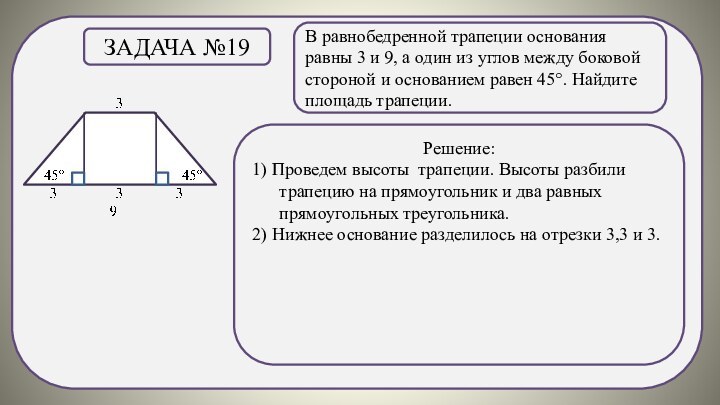
Задача №19
Решение:
1) Проведем высоты трапеции. Высоты разбили трапецию на прямоугольник и два равных прямоугольных треугольника.
2) Нижнее основание разделилось на отрезки 3,3 и 3.
Задача №19
Решение:
1) Проведем высоты трапеции. Высоты разбили трапецию на прямоугольник и два равных прямоугольных треугольника.
2) Нижнее основание разделилось на отрезки 3,3 и 3.
3) Каждый из прямоугольных треугольников
является равнобедренным, поэтому высота равна 3.
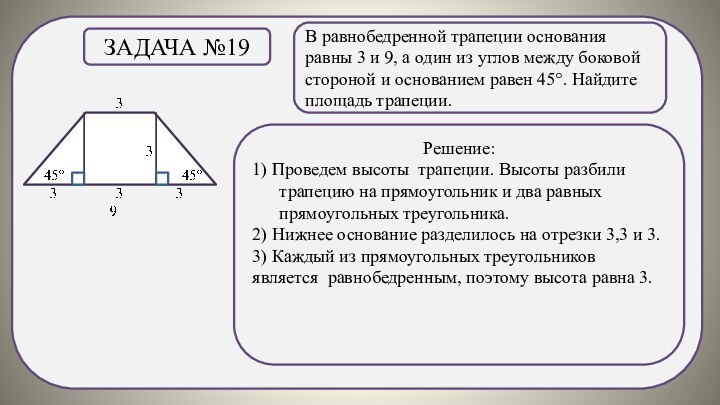
Задача №19
Решение:
1) Проведем высоты трапеции. Высоты разбили трапецию на прямоугольник и два равных прямоугольных треугольника.
2) Нижнее основание разделилось на отрезки 3,3 и 3.
3) Каждый из прямоугольных треугольников
является равнобедренным, поэтому высота равна 3.
Ответ: 18.