Слайд 2
Мы с вами уже знаем, что на любое
тело массой m, которое находится вблизи поверхности Земли, всегда
действует сила тяжести: Fт= mg.
Эта сила обусловлена притяжением Земли. Таким образом, Земля действует на тело, притягивая его к себе.
Слайд 3
По третьему закону Ньютона тело тоже притягивает к
себе Землю с такой же по модулю силой. Значит,
Земля и тело, находящееся вблизи ее поверхности, притягиваются др к др. Ньютон предположил, а потом и доказал, что не только Земля и любое тело вблизи ее поверхности, но и все тела во Вселенной притягиваются друг к другу.
Слайд 4
Все тела во Вселенной притягиваются друг к другу.
Силы этого притяжения называют силами всемирного тяготения или гравитационными
силами.
Слайд 5
Нужно определить, от чего зависит гравитационные силы взаимодействия
двух тел.
Рассмотрим знакомую схему силу тяжести Fт=mg, действующую на
тело массой m вблизи поверхности Земли. Ее модуль всегда пропорционален массе того тела, на которое она действует: Fт~m.
Тогда сделаем вывод: гравитационная сила всегда пропорциональна массе этого тела, на которое она действует.
Слайд 6
Гравитационная сила всегда пропорциональна массе этого тела, на
которое она действует.
Но так же эта сила является силой
взаимодействия двух тел.
По третьему закону Ньютона со стороны тела массой m на Землю действует такая же по модулю сила притяжения. Эта сила должна быть пропорциональна и массе Земли М, т.е. пропорциональна массе второго тела, который принимает участие в гравитационном взаимодействии: F~М
Слайд 7
Если в гравитационном взаимодействии участвуют два тела массами
m и М, то модуль силы этого взаимодействия пропорционален
произведению масс этих тел: F~m*M
Чтобы понять вид этой зависимости, Ньютон предположил, что движение Луны вокруг Земли происходит под действием силы тяготения
Fт со стороны Земли.
Другими словами, Земля действует на Луну с гравитационной силой, как и на любое тело, летящее вблизи ее поверхности.
Слайд 8
В результате гравитационного действия со стороны Земли и
тело (например, камень), и Луна приобретают ускорения. Модули этих
ускорений различны. Это предположительно обусловлено существенным различием в расстояниях от центра Земли до камня и до центра Луны.
Слайд 9
Ускорение, приобретаемое камнем- это ускорение g. Ускорение Луны
можно определить, зная траекторию ее движения. Во времена Ньютона
траектория Луны была хорошо известна из наблюдений по астрономии.
Благодаря этим наблюдениям, мы смогли определить ускорение Луны.
Его модуль оказался примерно в 3600 раз меньше, чем модуль g ускорения свободного падения вблизи поверхности Земли. Расстояние от центра Земли до центра Луны приблизительно в 60 раз больше расстояния от центра Земли до ее поверхности. Значит, увеличение расстояния в 60раз приводит к уменьшению ускорения, сообщаемого гравитационной силой, в 3600 раз.
Слайд 13
G- универсальная постоянная, которая называется гравитационной постоянной.
В настоящее
время она равна 6,67 *10^-11 Н*м^2/кг^2
Слайд 17
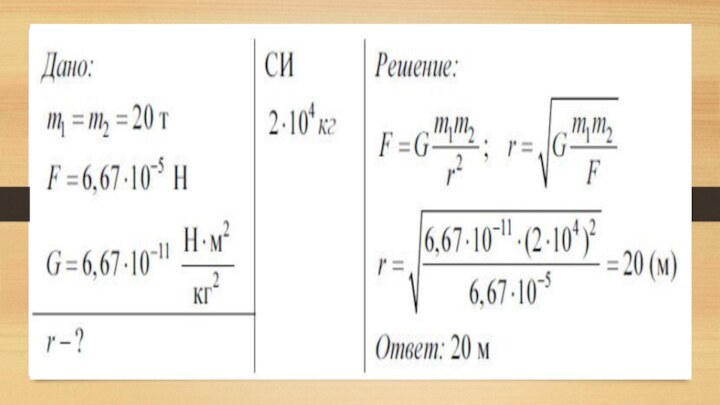
1. На каком расстоянии друг от друга находятся
два одинаковых шара массами по 20 т, если сила
тяготения между ними 6,67•10-5 Н?
Слайд 19
2.Масса Сатурна 5,7•10^26 кг, а его радиус— 6•10^7
м. Определите ускорение свободного падения на Сатурне.
Слайд 21
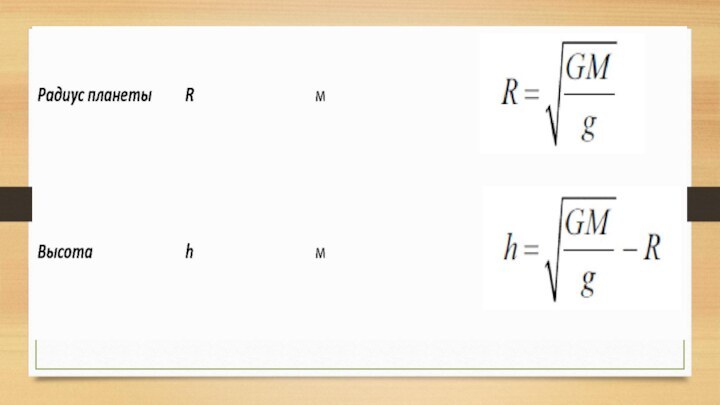
3. Чему равно ускорение свободного падения на высоте
над поверхностью Земли, равной двум ее радиусам?
Слайд 23
4. На какой высоте над поверхностью Земли сила
тяготения в 2 раза меньше, чем на поверхности Земли?
Слайд 26
6.Во сколько раз сила притяжения между Луной и
Солнцем больше, чем сила притяжения между Луной и Землей?
Слайд 28
7. При опытной проверке закона всемирного тяготения сила
взаимодействия между двумя свинцовыми шарами массами m1 = 5
кг и m2 = 500 г, расстояние между центрами которых r = 7 см, оказалась равной F = 34 нН. Вычислите по этим данным гравитационную постоянную.
Слайд 29
Согласно закону всемирного тяготения │F│=G*(??∗??)/?^?
Из этого выражения
следует, что
Подставим в эту формулу
результаты опыта, при этом все данные переведём в СИ: m2 = 500 г = 5 • 10-1 кг, r = 7 см = 7 • 10-2 м, F = 34 нН = 3,4 • 10-8 Н.
Слайд 30
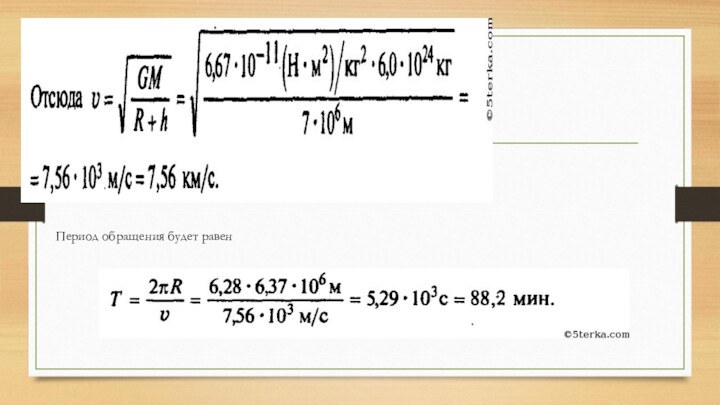
9. Какую скорость должен иметь искусственный спутник, чтобы
обращаться по круговой орбите на высоте 630 км над
поверхностью Земли? Каков период его обращения? (Спутник запускается в направлении с севера на юг.)
Слайд 31
Спутник вращается под действием силы тяжести Земли
которая в
данном случае является центростремительной силой. Так как
Слайд 33
10. Вычислите ускорение свободного падения и первую космическую
скорость у поверхности Луны.
Слайд 34
Ускорение свободного падения у поверхности Луны находим по
формуле
Первая космическая скорость на Луне равна
Слайд 35
11. Масса Луны в 81,3 раза а диаметр
в 3,67 раза меньше земных. Во сколько раз вес
астронавта был меньше на Луне, чем на Земле?
Слайд 36
F = G*Mm/R^2 - пусть с такой силой
человек притягивается к Земле.
М - масса Земли, m масса
астронавта, G - универсальная гравитационная постоянная, R - расстояние между центрами масс объектов (в данном случае приблизительно равен радиусу Земли) .
Астронавт притягивается к Луне с силой:
F2 = G(M/81,3)/(R/3,67)^2 = (3,67)^2/81,3*F = 0.166*F
Отношение сил притяжения:
F/F2 = 1/0.1657 = 6.035
Ответ: примерно в 6 раз
Слайд 37
12. Масса Юпитера равна 1,9 ∙ 1027 кг,
а его средний радиус — 70000 км. Определите ускорение
свободного падения вблизи поверхности планеты. Какую минимальную скорость нужно сообщить телу на Юпитере, чтобы оно стало искусственным спутником?
Слайд 39
Задача 13. Юпитер обладает массой 1,9*10^27 и радиусом
69 911 км. Определите ускорение свободного падения на Юпитере.
Слайд 41
M=1,9*10^27 кг
R=69911км
Fт=mg
F=G* M*m/R^2
mg=G*M*m/R^2
g=G*M/R^2=6,67*10^-11*1,9*10^27/69911000^2=25,9
м/с^2
Слайд 42
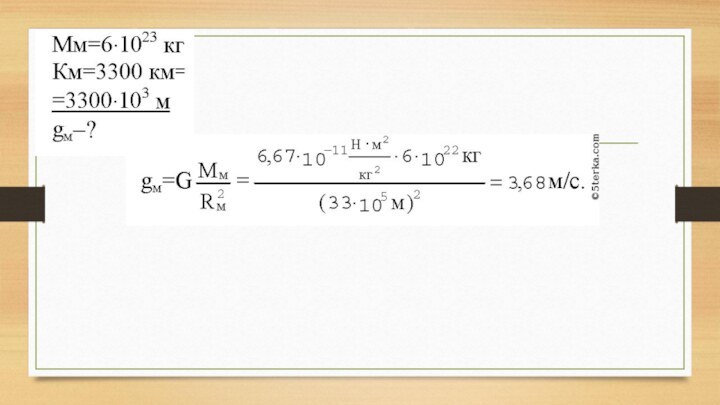
14.Вычислите ускорение свободного падения тел вблизи поверхности Марса.
Масса Марса равна 6⋅1023 кг, его радиус 3300 км.
Слайд 44
15.Найдите силу притяжения, действующую на тело вблизи поверхности
Луны. Масса тела 1 кг. Во сколько раз эта
сила отличается от силы тяжести, действующей на то же тело у поверхности Земли?
Слайд 47
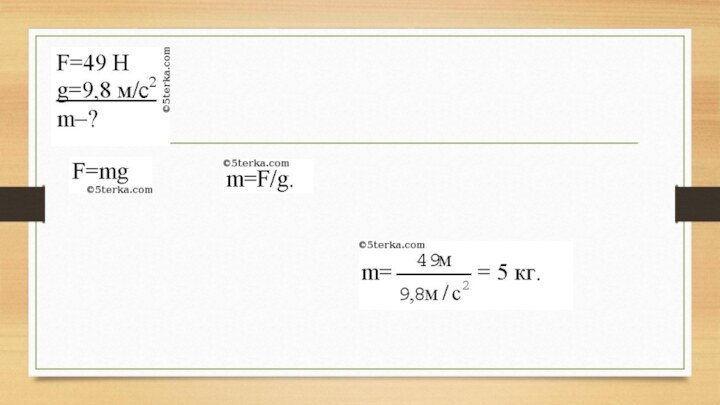
16. Какова масса тела, если сила тяжести, действующая
на него, равна 49 Н? Тело находится вблизи поверхности
Земли.
Слайд 49
17. Космонавт высадился на Луну. Его притягивают и
Луна и Земля. Во сколько раз сила притяжения космонавта
к Луне больше, чем к Земле? Радиус Луны равен 1730 км.