грамматикой архитектора»
Ле КорбюзьеЛе Корбюзье (1887 -1965гг.)
французский архитектор, художник, дизайнер
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Законы красоты в архитектуре Воронежа и Воронежской области
Содержание
- 2. «Прошли века, но роль геометрии не изменилась.
- 3. Могут ли архитекторы обойтись без знания математических законов при построении архитектурных шедевров?
- 4. Архитектура окружает нас везде, формирует эстетическую городскую
- 5. Цель : исследовать применение и роль математических
- 6. Гипотеза. Все архитектурные строения выполняются по законам
- 7. Практическая значимость: данный материал можно использовать для
- 8. Основные этапы работы
- 9. Архитектура — искусство и наука строить, проектировать здания и сооружения.Воронежский дворец
- 10. Архитектура зарождается вместе с человечеством, сопровождает его
- 11. Египетские пирамиды
- 12. Многогранник- это часть пространства, ограниченная плоскими многоугольниками- гранями.
- 13. Пирамида - многогранник, одна из граней которого
- 14. Многогранник, две грани которого - равные n-угольники, лежащие
- 15. Параллелепипед - шестигранник, противоположные грани которого попарно параллельны. ПараллелепипедБизнес центр Галереи ЧижоваГлавное здание управления ЮВЖД
- 16. Рамонский замокпос. Рамонь, Воронежская область
- 17. Многогранник называется правильным, если все его грани
- 18. ДодекаэдрПарк ДинамоДодекаэдр - это правильный многогранник, составленный из двенадцати равносторонних пятиугольников.
- 19. Гекса́эдр (куб) - шестигранник, все грани которого равны.Успенский Адмиралтейский храм
- 20. Церковь Вознесения ГосподняУсеченной пирамидой называется многогранник, у которого вершинами
- 21. Тела вращенияТелом вращения называют пространственную
- 22. ЦилиндрБизнес центр Премьер
- 23. Здание казначействагостиница «Mercure Воронеж Центр» Областной суд
- 24. ШарПамятник «Чупа-Чупсу» Стела "Слава советской науке" (памятник ДНК)
- 25. Кривые второго порядкаЭллиптический параболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением«Ротонда » здание Воронежской областной клинической больницы 1930-х годов,
- 26. Покровский Кафедральный собор Городская клиническая больница имени Пирогова
- 27. Смотровая на Спортивной набережной
- 29. Невырожденные кривые второго порядкаэллипсокружностьгиперболапарабола
- 30. Центральный стадион профсоюзов
- 31. Адмиралтейская площадьХрам Ксении ПетербургскойЗдание музея им. И.Крамского
- 32. Наиболее распространёнными геометрическими преобразованиями является симметрия. В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота».
- 33. Виды геометрических симметрийВиды симметрий, возможных для геометрического
- 34. Центральная симметрияХарактеризуется наличием центра симметрии — точки
- 35. Зеркальная симметрияТеатр оперы и балетаЭто отображение пространства
- 36. Зеркальная симметрияЗдание Воронежского областного краеведческого музеяЗдание администрации Воронежской области
- 37. Переносная симметрияДом с совой, на улице Алексеевского,
- 38. Результатом работы является интеллектуальный, творческий продукт, устанавливающий взаимосвязь математики и архитектуры.
- 39. Вывод:Поставленная цель достигнута. Мы убедились, что геометрия
- 40. Скачать презентацию
- 41. Похожие презентации
«Прошли века, но роль геометрии не изменилась. Она по-прежнему остается грамматикой архитектора»
Слайд 2 «Прошли века, но роль геометрии не изменилась. Она по-прежнему остается
грамматикой архитектора»
Ле КорбюзьеСлайд 3 Могут ли архитекторы обойтись без знания математических законов
при построении архитектурных шедевров?
Слайд 4 Архитектура окружает нас везде, формирует эстетическую городскую среду.
Наше настроение, мироощущение зависят от того, какие здания и
сооружения нас окружают. В наше время города и страны все более застраиваются. Появляются новые сооружения и направления в архитектуре, поэтому назрела необходимость исследования того многообразия объектов, которые появились в нашем мире. Это и обуславливает актуальность выбранной темы.Слайд 5 Цель : исследовать применение и роль математических закономерностей
и геометрических фигур в создании произведений архитектурного искусства.
Слайд 6 Гипотеза. Все архитектурные строения выполняются по законам геометрии,
в основе которых лежат геометрические формы. Комбинации этих форм
и использование их свойств способствуют созданию эстетического архитектурного сооружения.
Слайд 7
Практическая значимость: данный материал можно использовать для привития
интереса к математике; способствует углублению математических знаний, выходящих за
рами школьной программы и формированию представления о прикладных возможностях математики.
Слайд 9
Архитектура — искусство и наука строить, проектировать здания и сооружения.
Воронежский дворец
Слайд 10 Архитектура зарождается вместе с человечеством, сопровождает его в
историческом развитии. В ней отражаются мировоззрение, ценности, знания людей,
живших в различные исторические эпохи.менгиры
дольмены
кромлехи
Слайд 13 Пирамида - многогранник, одна из граней которого -
произвольный многогранник, а остальные грани - треугольники, имеющие одну
общую вершину.Пирамида
Памятник воинской Славы "Пирамида"
Слайд 14 Многогранник, две грани которого - равные n-угольники, лежащие в
параллельных плоскостях, а остальные n граней - параллелограммы, называется n-угольной призмой.
Призма
Ильинская
церковьСайт
Маршрут
Сохранить
Ильинская церковь
Слайд 15
Параллелепипед - шестигранник, противоположные грани которого попарно параллельны.
Параллелепипед
Бизнес
центр Галереи Чижова
Главное здание управления ЮВЖД
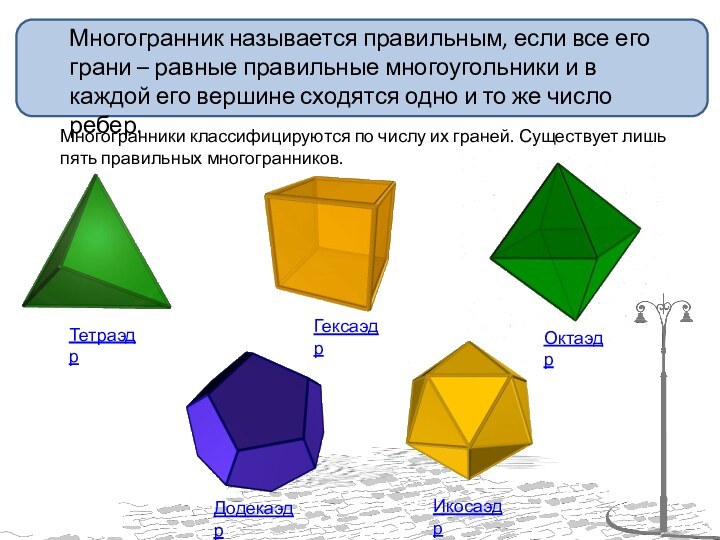
Слайд 17 Многогранник называется правильным, если все его грани –
равные правильные многоугольники и в каждой его вершине сходятся
одно и то же число ребер.Многогранники классифицируются по числу их граней. Существует лишь пять правильных многогранников.
Тетраэдр
Октаэдр
Гексаэдр
Додекаэдр
Икосаэдр
Слайд 18
Додекаэдр
Парк Динамо
Додекаэдр - это правильный многогранник, составленный из
двенадцати равносторонних пятиугольников.
Слайд 20
Церковь Вознесения Господня
Усеченной пирамидой называется многогранник, у которого вершинами служат
вершины основания и вершины ее сечения плоскостью, параллельной основанию.
Усеченная пирамида
Слайд 21
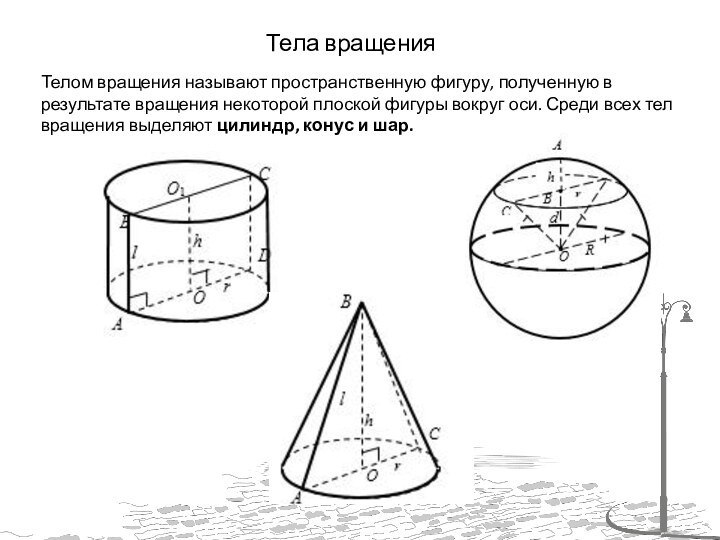
Тела вращения
Телом вращения называют пространственную фигуру,
полученную в результате вращения некоторой плоской фигуры вокруг оси.
Среди всех тел вращения выделяют цилиндр, конус и шар.
Слайд 25
Кривые второго порядка
Эллиптический параболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых
координатах уравнением
«Ротонда »
здание Воронежской областной клинической больницы 1930-х годов,
Слайд 28
Кривая второго порядка
Параболический цилиндр — цилиндрическая поверхность второго порядка, для которой образующей служит парабола. Ее получают при перемещении параболы по направляющей прямой.
Слайд 32 Наиболее распространёнными геометрическими преобразованиями является симметрия. В древности слово «СИММЕТРИЯ» употреблялось
в значении «гармония», «красота».
Слайд 33
Виды геометрических симметрий
Виды симметрий, возможных для геометрического объекта,
зависят от множества доступных геометрических преобразований и того, какие
свойства объекта должны оставаться неизменными после преобразования.Центральная симметрия
Зеркальная симметрия
Переносная симметрия
Слайд 34
Центральная симметрия
Характеризуется наличием центра симметрии — точки O,
обладающей определенным свойством: точка O является центром симметрии, если
при повороте вокруг нее на 180° фигура переходит сама в себя. Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм.Памятник воинской Славы «Ротонда»
Слайд 35
Зеркальная симметрия
Театр оперы и балета
Это отображение пространства на
себя, при котором любая точка переходит в симметричную ей
точку, относительно плоскости. Зеркально симметричным считается объект, состоящий из двух половинок, которые являются зеркальными двойниками по отношению друг к другу.
Слайд 36
Зеркальная симметрия
Здание Воронежского областного краеведческого музея
Здание администрации Воронежской
области
Слайд 37
Переносная симметрия
Дом с совой, на улице Алексеевского, 12
Состоит
в том, что части целой формы организованы таким образом,
что каждая следующая повторяет предыдущую и отстоит от неё на определённый интервал в определённом направлении.Слайд 38 Результатом работы является интеллектуальный, творческий продукт, устанавливающий взаимосвязь
математики и архитектуры.
Слайд 39
Вывод:
Поставленная цель достигнута. Мы убедились, что геометрия играет
