Слайд 2
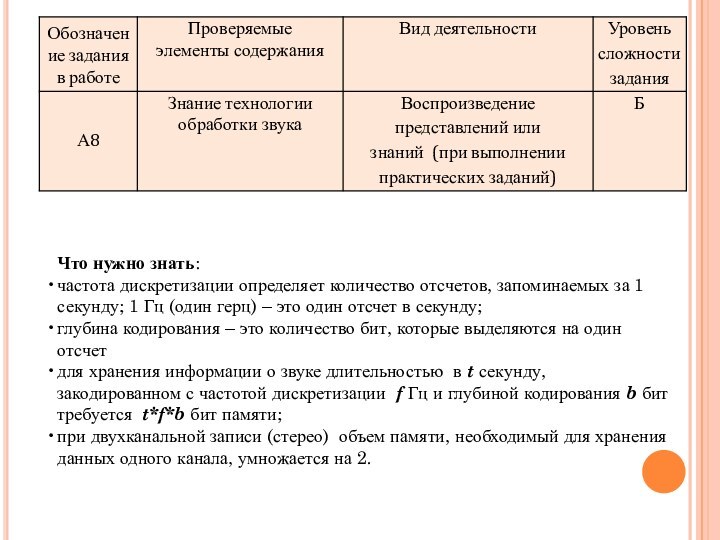
Что нужно знать:
частота дискретизации определяет количество отсчетов, запоминаемых
за 1 секунду; 1 Гц (один герц) – это
один отсчет в секунду;
глубина кодирования – это количество бит, которые выделяются на один отсчет
для хранения информации о звуке длительностью в t секунду, закодированном с частотой дискретизации f Гц и глубиной кодирования b бит требуется t*f*b бит памяти;
при двухканальной записи (стерео) объем памяти, необходимый для хранения данных одного канала, умножается на 2.
Слайд 3
Пример задания:
Производится одноканальная (моно) звукозапись с частотой дискретизации
8 кГц и глубиной кодирования 16 бита. Запись длится
2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?
1) 1 2) 2 3) 3 4) 4
8кГц=23*125*23=26*125Гц 2минуты=2*15*22=15*23
26*125*15*23*24
223
213*125*15
223
=
=
125*15
210
≈ 2
Слайд 4
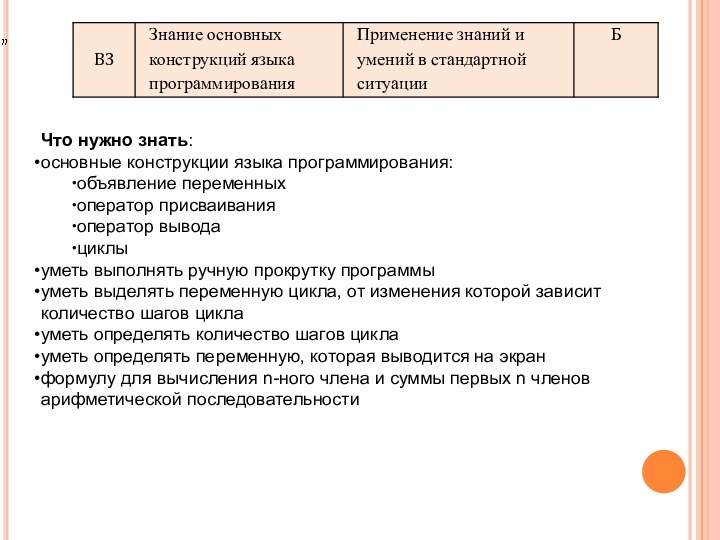
Что нужно знать:
основные конструкции языка программирования:
объявление переменных
оператор присваивания
оператор
вывода
циклы
уметь выполнять ручную прокрутку программы
уметь выделять переменную цикла, от
изменения которой зависит количество шагов цикла
уметь определять количество шагов цикла
уметь определять переменную, которая выводится на экран
формулу для вычисления n-ного члена и суммы первых n членов арифметической последовательности
Слайд 5
Пример задания:
Определите, что будет напечатано в результате работы
следующего фрагмента программы:
Var k, s : integer;
BEGIN
s:=0;
k:=0;
while s
103
Слайд 6
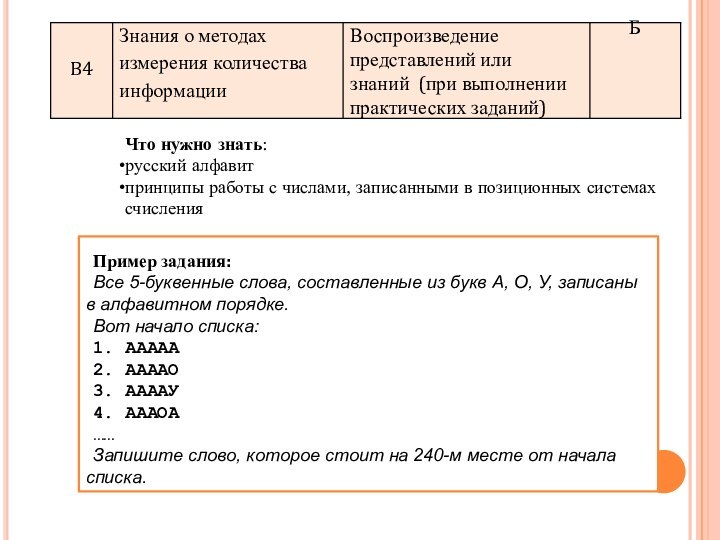
Что нужно знать:
русский алфавит
принципы работы с числами, записанными
в позиционных системах счисления
Пример задания:
Все 5-буквенные слова, составленные из
букв А, О, У, записаны в алфавитном порядке.
Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
……
Запишите слово, которое стоит на 240-м месте от начала списка.
Слайд 7
Решение ( идея М. Густокашина):
по условию задачи важно
только то, что используется набор из трех разных символов,
для которых задан порядок (алфавитный); поэтому для вычислений можно использовать три любые символа, например, цифры 0, 1 и 2 (для них порядок очевиден – по возрастанию)
выпишем начало списка, заменив буквы на цифры:
1. 00000
2. 00001
3. 00002
4. 00010
……
это напоминает (в самом деле, так оно и есть!) числа, записанные в троичной системе счисления в порядке возрастания: на первом месте стоит число 0, на втором – 1 и т.д.
тогда легко понять, что 240-м месте стоит число 239, записанное в троичной системе счисления
переведем 239 в троичную систему: 239 = 222123
заменяем обратно цифры на буквы: 22212 УУУОУ
Ответ: УУУОУ.
Слайд 8
Еще пример задания (автор – В.В. Путилов):
Все 5-буквенные
слова, составленные из 5 букв А, К, Л, О,
Ш, записаны в алфавитном порядке.
Вот начало списка:
1. ААААА
2. ААААК
3. ААААЛ
4. ААААО
5. ААААШ
4. АААКА
……
На каком месте от начала списка стоит слово ШКОЛА?
Решение:
по аналогии с предыдущим решением будем использовать пятеричную систему счисления с заменой А 0, К 1, Л 2, О 3 и Ш 4
слово ШКОЛА запишется в новом коде так: 413205
переводим это число в десятичную систему:
413205 = 454 + 153 + 352 + 251 = 2710
поскольку нумерация элементов списка начинается с 1, а числа в пятеричной системе – с нуля, к полученному результату нужно прибавить 1, тогда…
Ответ: 2711.
Слайд 9
Что нужно знать:
операции целочисленного деления (div) и взятия
остатка (mod)
как работают операторы присваивания, циклы и условные операторы
в языке программирования
Пример задания:
Ниже на 2-х языках записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 7.
Слайд 11
Что нужно знать:
если в город R можно приехать
только из городов X, Y, и Z, то число
различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть
где обозначает число путей из вершины A в некоторую вершину Q
число путей конечно, если в графе нет циклов – замкнутых путей
Слайд 12
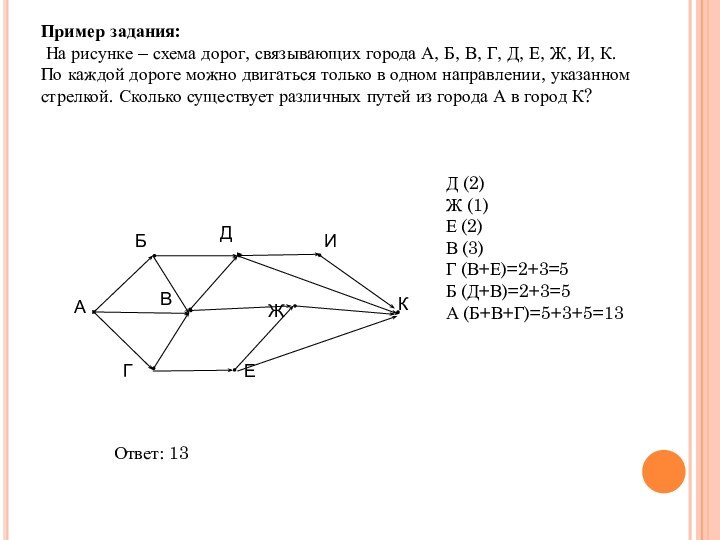
Пример задания:
На рисунке – схема дорог, связывающих
города А, Б, В, Г, Д, Е, Ж, И,
К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Ответ: 13
Д (2)
Ж (1)
Е (2)
В (3)
Г (В+Е)=2+3=5
Б (Д+В)=2+3=5
А (Б+В+Г)=5+3+5=13
Слайд 13
Что нужно знать:
уметь строить дерево решений
уметь искать одинаковые
числа в списке
уметь считать разные числа в списке
Пример задания:
У
исполнителя Калькулятор две команды:
1. прибавь 3,
2. вычти 2.
Первая из них увеличивает число на экране на 3, вторая – уменьшает его на 2 (отрицательные числа допускаются).
Программа для Калькулятора – это последовательность команд. Сколько различных чисел можно получить из числа 1 с помощью программы, которая содержит ровно 5 команд?
Слайд 14
Что нужно знать:
функция – это вспомогательный алгоритм, который
возвращает некоторое значение–результат
цикл для поиска наибольшего значения выглядит точно
так же, только знак < нужно заменить на знак >
если функция представляет собой квадратный трехчлен вида то абсцисса, соответствующая точке минимума, вычисляется по формуле
если квадратный трехчлен задан в виде , то абсцисса, соответствующая точке минимума, вычисляется по формуле
Слайд 15
Пример задания:
Определите, какое число будет напечатано в результате
выполнения следующего алгоритма
Бейсик Паскаль
Слайд 16
Обзор интернет ресурсов
по подготовке к ЕГЭ
http://scro.ru
http://www.it-n.ru
http://fipi.ru
http://ege.yandex.ru
http://kpolyakov.narod.ru
http://ege-go.ru