- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Развитие пространственных представлений и формирование геометрических понятий у учащихся начальной школы
Содержание
- 2. Представление опыта работыРазвитие пространственных представлений и формирование геометрических понятий у учащихся начальной школы
- 3. «Обучение геометрии может иметь смысл, если только
- 4. Цель – формирование пространственных представлений у младших
- 5. АктуальностьПространственные представления и пространственное воображение ребенка являются
- 6. АктуальностьРазвитие пространственных представлений является важнейшей частью интеллектуального
- 7. Наличие хорошего пространственного воображения необходимо и инженеру,
- 8. Научная обоснованность Формирование пространственных представлений у младших
- 9. Технология Методы обучения младших школьников, определяются, прежде
- 10. ТехнологияОперирование пространственными образами:Преобразуется пространственное положение и не
- 11. Технология. Виды работ. Формирование пространственных представлений с
- 12. Виды работ в 1 классе
- 13. Виды работ 2-4 классов
- 14. Технология Использование межпредметных связей на уроке
- 15. Задание: используя узоры народных промыслов, придумай и
- 16. Работы учеников 2 и 4 классов
- 17. Раскрась кольца пирамидки, если желтое кольцо находится
- 18. По щучьему велению ведра с
- 19. Мартышка, попугай, слоненок и удав
- 20. Два дома соединены пешеходными дорожками.
- 21. Дорисуй флажки, соблюдая закономерность их расположения .
- 22. Катя, Маша и Петя нарисовали пейзажи, которые
- 23. Упражнения на развитие умений представить мысленно различные
- 24. • •
- 25. Задачи на превращения геометрических фигур. На первом
- 26. Задание: найдите закономерность и угадай, какая следующая фигура, нарисуй её.
- 27. Какую фигуру справа можно получить при складывании
- 28. Задания на подборку фигуры заданной формы и
- 29. Какая фигура расположена слева? Как называется
- 30. Какая фигура, не имеющая объема, находится в
- 31. Условия эффективностиФормирование пространственных представлений должно отводиться постоянное
- 32. Результативность Таким образом, неизбежно вытекает
- 33. Результативность
- 34. Потенциальные возможностиИз курсов педагогики и методики математики
- 35. Скачать презентацию
- 36. Похожие презентации
Представление опыта работыРазвитие пространственных представлений и формирование геометрических понятий у учащихся начальной школы

































Слайд 2
Представление
опыта работы
Развитие пространственных представлений и формирование геометрических
понятий у учащихся
Слайд 3 «Обучение геометрии может иметь смысл, если только используются
связи с привычным пространством».
Г. Фройденталь (немецкий математик)
Формирование пространственных представлений
выстраиваются в сознании ребенка уже с самого раннего детства . Однако в связи с тем, что «владение пространственными представлениями и наличие пространственного воображения … являются одним из основных критериев образованности учащегося в области математики», как утверждал известный социальный психолог Г.Гибш, задача формирования этого вида мышления традиционно считается одной из задач математического образования ребенка.
Столь же традиционно эта задача связывается с изучением геометрического материала, как в начальной, так и в средней школе.
Слайд 4 Цель – формирование пространственных представлений у младших школьников.
Задачи:
Проанализировать систему формирования геометрических представлений в курсе математики начальной
школы; Развивать пространственные представления у младших школьников;
Знакомить ребенка с органическими для него геометрическими методами познания как естественной составляющей математических методов;
Готовить младших школьников к усвоению понятия о пространственности реального мира.
Слайд 5
Актуальность
Пространственные представления и пространственное воображение ребенка являются предпосылками
для формирования его пространственного мышления и обеспечиваются различными психическими
процессами, такими как восприятие (первоосновой которого являются ощущения), внимание, память, воображение при обязательном участии речи. Ведущую роль при этом играют логические приемы мышления: сравнение, анализ, синтез, классификация, обобщение, абстрагирование.
Слайд 6
Актуальность
Развитие пространственных представлений является важнейшей частью интеллектуального развития
в целом, поскольку играет большую роль не только при
изучении геометрии, но и других учебных дисциплин.Без сформированных пространственных представлений невозможно эффективное изучение рисования, черчения, физики, географии, технологии и ряда других школьных предметов.
Наличие хорошего пространственного воображения необходимо и инженеру, и дизайнеру, и компьютерщику, и экономисту и специалистам многих других профессий.
Слайд 7 Наличие хорошего пространственного воображения необходимо и инженеру, и
дизайнеру, и компьютерщику, и экономисту и специалистам многих других
профессий.Костюм с использованием элементов батика выполнен Лаврентьевой Н.В.
Слайд 8
Научная обоснованность
Формирование пространственных представлений у младших школьников
способствует развитию восприятия, памяти, внимания, выработке у младших школьников
математических понятий.Переход от наглядно-образного к наглядно-действенному мышлению требует сложной аналитико-синтетической работы, выделения деталей, сопоставления их друг с другом.
В этом процессе большое значение принадлежит и речи, которая помогает назвать признак, сопоставить признаки.
Только на основе развития наглядно-действенного и наглядно-образного мышления начинает формироваться формально-логическое мышление, которое является основой умственного развития младшего школьника.
Слайд 9
Технология
Методы обучения младших школьников, определяются, прежде всего,
особенностями познавательных возможностей детей, а также самим предметом геометрии
как науки о свойствах геометрических фигур.
Слайд 10
Технология
Оперирование пространственными образами:
Преобразуется пространственное положение и не затрагивается
структура образа;
Преобразуется структура образа путём различных трансформаций;
Исходный образ преобразуется
длительно и неоднократно.Слайд 11 Технология. Виды работ. Формирование пространственных представлений с первых
уроков 1 класса
раскрасить предметные картинки;
нарисовать «дорожку»;
обозначить предметы буквами;
сравнить
фигуры и найти лишнюю;вырезать и составить заданную фигуру из деталей;
измерь, начерти;
решить графическую или геометрическую головоломку и др.
Слайд 14
Технология
Использование межпредметных связей на уроке математики по развитию
графических умений (минутки графического творчества на уроках математики)
Слайд 15 Задание: используя узоры народных промыслов, придумай и нарисуй
свой узор. Работы учеников 1
класса 3 класса
Слайд 17
Раскрась кольца пирамидки, если желтое кольцо находится между
красным и синим кольцами, а синее между желтым и
зеленым
Слайд 18
По щучьему велению ведра с водой
ходят в избу сами так, что озеро всегда остается
от Емели справа. Нарисуй дорожку, по которой ходит Емеля
Слайд 19
Мартышка, попугай, слоненок и удав отправляются
в путешествие. «Все садятся в вагоны, следующие за моим»,
- приказала мартышка. «Я поеду между слоненком и удавом», - сказал попугай. «А я поеду за попугаем», - промолвил слоненок. Обозначьте нужной буквой вагон, в котором поедет каждый из друзей
Слайд 20
Два дома соединены пешеходными дорожками. Нарисуй
линией путь, по которому можно обойти все дорожки только
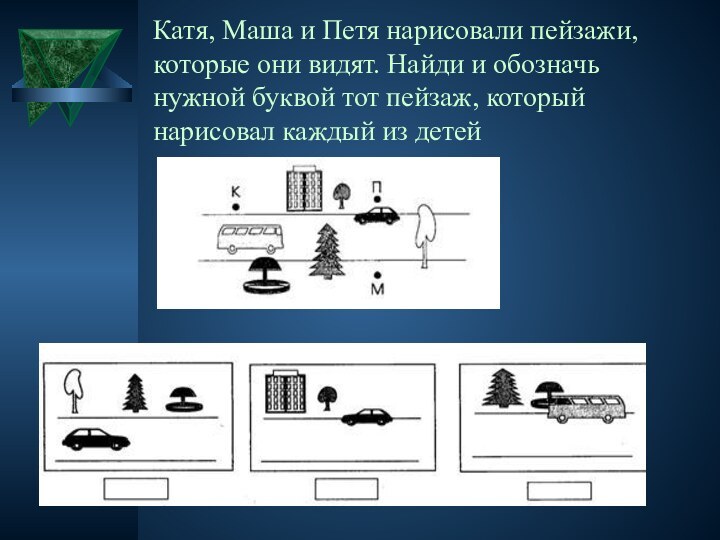
по одному разу, если прогулку надо начать и закончить у дома, изображенного слева.Слайд 22 Катя, Маша и Петя нарисовали пейзажи, которые они
видят. Найди и обозначь нужной буквой тот пейзаж, который
нарисовал каждый из детейСлайд 23 Упражнения на развитие умений представить мысленно различные положения
и форму предметов при изучении многогранников. Развитие таких умений
должно опираться на практические упражнения с развертками многогранников: - из данной развертки склеить куб ; - отметить на развертке одним цветом ребра, которые необходимо склеить, чтобы получить данную фигуру.Слайд 24 • • •
•
•
•
•
•
•
•
•
На доске или плакате рисуется несколько последовательностей лучей,
например
таких, какие изображены на рисунке.
С помощью вопросов типа:
Что интересное заметили?
Как меняется
направление линий?
и подобных детям
предлагается найти
закономерность
в каждом ряде и
продолжить этот ряд.
Слайд 25
Задачи на превращения геометрических фигур.
На первом этапе
работы с такими задачами ученики выполняют задания, используя фигуры,
вырезанные из цветного картона. На втором этапе, после приобретения соответствующих навыков, задания выполняются мысленно с последующей проверкой верности своего выбора путем сбора фигуры.Слайд 27 Какую фигуру справа можно получить при складывании данных
частей, расположенных слева;
Как называются выбранные вами фигуры? Чем они
похожи? Чем отличаются? Какие еще фигуры можно собрать из двух фигур, изображенных слева? и т.д.
Слайд 28 Задания на подборку фигуры заданной формы и размера
«Подбери заплатку».
Задания выполняются путем логического мышления; предположения детей проверяются
практически, так как все детали съёмные.
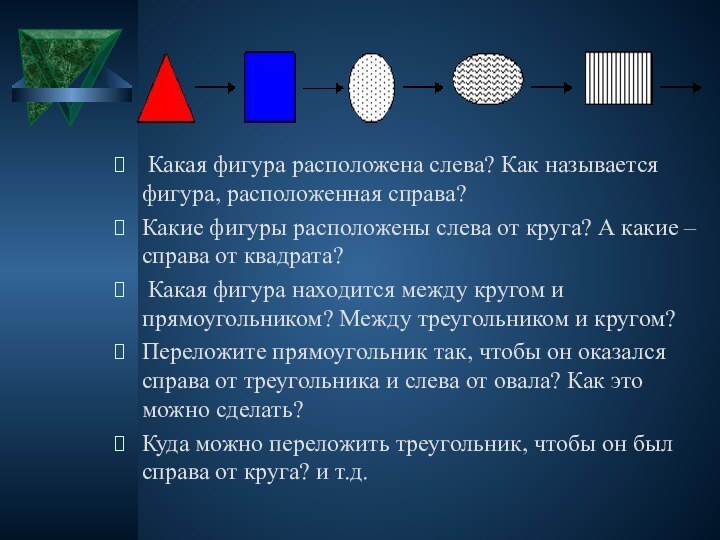
Слайд 29
Какая фигура расположена слева? Как называется фигура,
расположенная справа?
Какие фигуры расположены слева от круга? А какие
– справа от квадрата?Какая фигура находится между кругом и прямоугольником? Между треугольником и кругом?
Переложите прямоугольник так, чтобы он оказался справа от треугольника и слева от овала? Как это можно сделать?
Куда можно переложить треугольник, чтобы он был справа от круга? и т.д.
Слайд 30
Какая фигура, не имеющая объема, находится в верхнем
ряду?
Как нужно переставить фигуры, чтобы все плоские находились внизу?
Между
какими фигурами находится цилиндр?Назовите фигуры, расположенные выше красного треугольника и левее пирамиды?
Как переставить фигуры, чтобы квадрат стал выше и правее треугольника? И т.п.
Слайд 31
Условия эффективности
Формирование пространственных представлений должно отводиться постоянное внимание
не только на отдельных уроках (с ответствующими темами), а
в течение всего периода обучения математике в начальной школе, содержащих геометрический материал.При этом необходимо опираться на практическую деятельность учеников в сочетании с дидактически обоснованной игровой формой.
Слайд 32
Результативность
Таким образом, неизбежно вытекает вывод
о том, что, обучая младших школьников математике, необходимо так
ставить вопросы и организовывать познавательную деятельность, чтобы задания были направлены не только на формирование математических понятий, но и на развитие пространственного мышления детей, без которого невозможно развитие общеинтеллектуальных умений и навыков.
Слайд 34
Потенциальные возможности
Из курсов педагогики и методики математики известно,
что деятельность может быть репродуктивной и продуктивной.
Продуктивная деятельность
связана с активной работой мышления.Она находит своё выражение в таких операциях, как анализ и синтез, сравнение, классификация и обобщение.
Включение этих операций в процесс усвоения содержания обеспечивает реализацию продуктивной деятельности младших школьников.





























