Слайд 2
Новые знакомые Незнайки.
Однажды Знайка вышел из дома. Он

хотел прогуляться по городу, зайти в библиотеку. Не успел
он выйти, как навстречу ему Незнайка с рюкзаком. Знайка спросил у него, куда тот направляется. Незнайка рассказал, что он только что вернулся из похода, в который их водил Пулька. Знайка удивился и спросил почему его не взяли. Незнайке стало стыдно и он сказал Знайке, что сам о походе узнал в последний момент. Знайка стал интересоваться что интересного было в походе. Незнайка рассказал ему о всех впечатлениях от похода, но самым главным впечатлением было вот что:
-У меня появилось три новых друга! Самое интересное: каждый из нас познакомился ровно с тремя!- с восторгом рассказал он.
- А сколько вас всего было?- спросил Знайка.
- Сейчас сосчитаю: Пулька, Пончик, Чудик, Топик, Гунька, Носик, Гвоздик, Трубач и я. Всего девять человек.
Знайка покачал головой:
- Не может такого быть!
- Какого такого?- с подозрением спросил Незнайка.
- А такого, что каждый познакомился ровно с тремя малышами.
- Ну и ну,- возмутился Незнайка. – Тебя с нами не было, а ты говоришь так, как будто это вдел. Я познакомился с Чудиком, Топиком и Трубачом, Пулька- с носиком, Топиком и... я точно не помню! Но то что каждый познакомился с тремя это я точно знаю.
- Этого не может быть и я тебе это докажу путем логических рассуждений!
Слайд 3
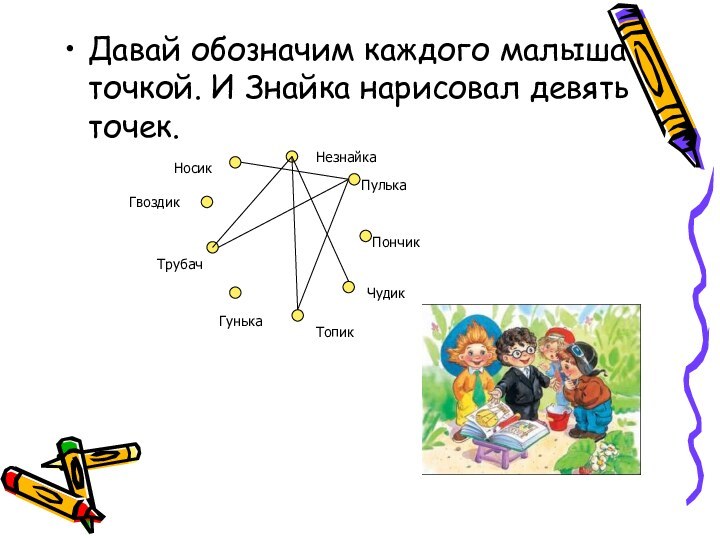
Давай обозначим каждого малыша точкой. И Знайка нарисовал
девять точек.
Незнайка
Пулька
Пончик
Чудик
Топик
Гунька
Трубач
Гвоздик
Носик
Слайд 4
-Так как Пулька познакомился с Носиком, то

Носик познакомился с Пулькой. Соединим эти точки между собой.
-
Но он же познакомился еще с Трубачем и... допустим с Топиком.
- Поэтому соединим Пулькину точку с Трубачевой и Топиковой.
- Я понял! Я тоже познакомился с тремя и от моей точки тоже должны отходить три линии!
- Соединим линией каждую пару новых знакомых,- предложил Знайка.
- Но я забыл кто с кем познакомился!
- Не беда. Мы докажем, что невозможно каждому познакомиться ровно с тремя.
- Опять ты за свое! Я же сказал, что я сам при этом был!
- Хорошо,- улыбнулся Знайка.- Предположим, что такие знакомства возможны. Если точки обозначают малышей, а линии – знакомства, то ты должен нарисовать картинку, где девять точек, а из каждой точки выходит по три линии.
- У меня не получается...- уныло произнес Незнайка.
- А у тебя и не получится, ты сказал, что каждый из малышей познакомился с тремя. Значит всех знакомств было 3 х 9= 27.
- Но если я познакомился с Топиком, то он познакомился со мной, значит знакомств было в два раза меньше!
- Конечно, - согласился Знайка.- На рисунке каждое знакомство соответствует линии между двумя точками. Значит на рисунке должно быть 27:2=13,5 линии.
- Но такого же не может быть!
- Правильно, не может, значит, и обязательных трех знакомств у каждого быть не может.
Незнайка задумался, хочешь - не хочешь, а Знайка прав.
- Ты помнишь что такое четное число?
- Конечно,- ответил Незнайка.
- А знаешь, что такое граф?
- Нет, но я помню только что граф это такой господин который жил в средние века в замке.
- Правильно. И наше слово тоже древнего происхождения: биография – жизнеописание; география – землеописание; графит- стержень для письма и т.д.
Слайд 5
Граф, про который мы сейчас говорим, состоит из
точек и линий, соединяющих некоторые пары точек. Точки называются
вершинами, а линии – ребрами. Две вершины, которые соединены ребром, называются смежными.
- Я понял! Та картинка, которую мы нарисовали , является графом! Вершины обозначают малышей, а ребра – знакомства между ними!
- Правильно, так давай нарисуем граф полностью!
Слайд 6
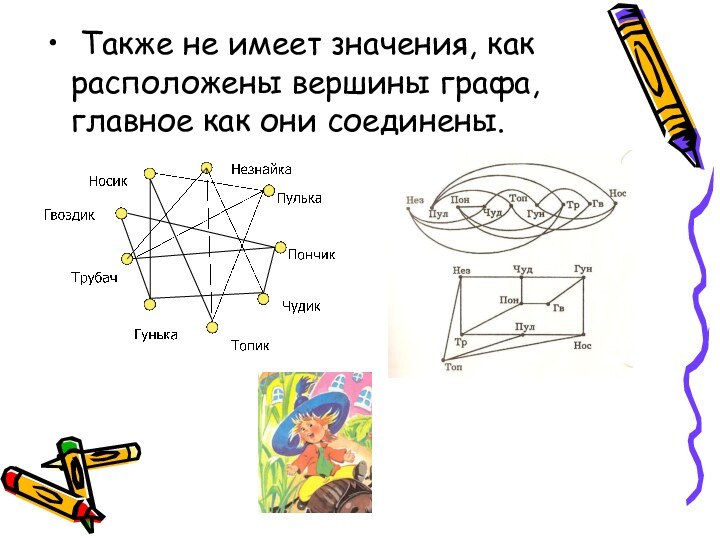
Также не имеет значения, как расположены вершины
графа, главное как они соединены.
Слайд 7
-Посмотрите: Носик познакомился с Пулькой, Топиком и Гунькой
и на первом и на втором и на третьем
рисунке. А если между Незнайкой и Пулькой нет линий на первом рисунке, то их нет и на втором и на третьем.Эти рисунки задают точно такой же граф знакомств.
Внимательно посмотрев, Незнайка убедился в том, что это правда.
- Такие графы называются изоморфными. Они устроены одинаково, хоть и нарисованы по разному.
- Я немного ошибся,- сказал Незнайка. – У всех по три знакомства а у гвоздика два.
- Давайте посмотрим на наш граф знакомств. Сложим числа знакомств всех малышей:
ЧИСЛО ЗНАКОМСТВ НЕЗНАЙКИ
+
ЧИСЛО ЗНАКОМСТВ ПУЛЬКИ
+
ЧИСЛО ЗНАКОМСТВ ПОНЧИКА
+
ЧСИЛО ЗНАКОМСТВ ГУНЬКИ
+
ЧИСЛО ЗНАКОМСТВ ТОПИКА
+
ЧИСЛО ЗНАКОМСТВ ЧУДИКА
+
ЧИСЛО ЗНАКОМСТВ ТРУБАЧА
+
ЧИСЛО ЗНАКОМСТВ ГВОЗДИКА
+
ЧИСЛО ЗНАКОМСТВ НОСИКА
_______________________________
Слайд 8
- Под чертой получилась сумма знакомств, а так
как каждое знакомство считается дважды, то у нас получилось
удвоенное число знакомств. Количество ребер, выходящих из вершины графа, называется степенью вершины.
Таким образом мы доказали теорему:
В графе сумма степеней вершин равна удвоенному количеству ребер.
Слайд 9
Это утверждение верно для графов с любым числом
вершин. Оно носит название леммы о рукопожатии. Лемма о
рукопожатии помогает доказать, что число вершин нечетной степени в любом графе четное.
Слайд 10
Шахматный турнир.
Однажды шел Незнайка по улице и
вдруг увидел объявление о начале шахматного матча. В списке
участвующих оказались 16 малышей. Незнайка предложил провести чемпионат города. Те, кто займет первые четыре места, составят команду. Каждый малыш должен будет сыграть партию с пятнадцатью. Состоится несколько партий в день.
Слайд 11
- Интересно, а сколько при круговой системе пришлось
бы сыграть партий?- спросил Шпунтик.
-Число партий легко подсчитать,- сказал
Знайка и нарисовал 16 точек.-16 точек- это 16 шахматистов.
Слайд 12
-Если два шахматиста играют между собой, соединим их
точки линией. Т.к. каждый играет с каждым мы соединим
каждую точку с остальными, но у нас их 16, поэтому сначала нарисуем с восемью.
Слайд 13
Точки(вершины) этого графа – шахматисты, а ребра

– партии. Такой граф, в котором каждая вершина соединена
со всеми остальными называется полным. Если мы хотим узнать, сколько партий сыграют восемь шахматистов, мы должны подсчитать число ребер в полном графе с восемью вершинами.
- Что здесь считать, - сказал Торопыжка. Из каждой точки выходят семь линий, значит, всего линий будет 8 х 7= 56
-Поспешишь людей насмешишь! Ведь каждая линия выходит из двух точек, значит ты сосчитал ее два раза, а нужно было всего один! Но эту проблему легко решить: разделим полученное число на два, в этом графе 28 ребер.
- Правильно, давайте посчитаем, сколько ребер будет в полном графе с шестнадцатью вершинами?
- Любая точка соединена с пятнадцатью другими: 16 х 15= 240. Я тоже посчитал каждую линию дважды, 240 делим на 2, получаем 120 линий. Нам нужно сыграть 120 партий. Понадобится семь с половиной дней, если каждый день будут играть по две партии.
- Многовато,- сказал Незнайка.
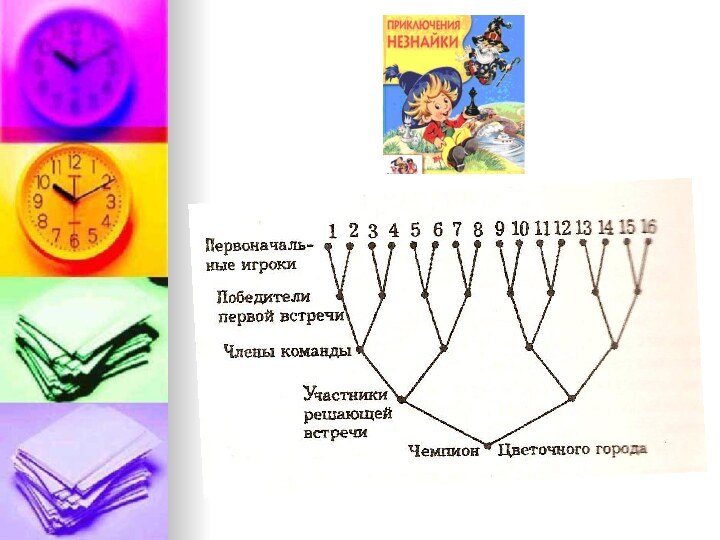
- Поэтому я предлагаю другую систему: олимпийскую. Шестнадцать малышей разобьем на восемь пар. Малыши в каждой паре встречаются между собой. Восемь победителей составят четыре новые пары. После встречи в этих парах останутся четыре малыша, которые и войдут в команду. А еще через две встречи мы и узнаем, кто чемпион нашего города. Олимпийскую систему можно изобразить следующим графом:
Слайд 15
Такой граф называется корневым деревом.
- Если вам
не нравится такая система то я могу предложить другую,
- заговорил Знайка- Шестнадцать игроков делятся на четыре группы по четыре игрока в группе. В группе каждый малыш играет с каждым. Победители групп образуют команду. Они же разыграют звание чемпиона.
Знайка нарисовал такую схему:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Слайд 16
Получилось четыре полных графа с четырьмя вершинами
каждый.
- Да, - согласился Знайка.- можно считать, что на
этом рисунке нарисованы четыре графа, но можно считать, что это один граф, состоящий из частей, каждые части графа называются компонентой. Если от одной вершины графа до другой можно перейти по ребрам, то эти вершины принадлежат одной компоненте, а если нельзя, то разным.
Слайд 17
- А если от каждой вершины можно
по ребрам перейти к любой другой, то у графа
будет одна компонента?- спросил Незнайка.
- Конечно. Такой граф называется связным. А если граф имеет больше чем одну компоненту, то он называется несвязным.
-Каждому малышу придется сыграть по три встречи, - продолжил Знайка.
-Три раза не будет, а один – возможно. Кроме того, те малыши, которые окажутся в одной группе с тобой, имеют мало шансов попасть в команду.
Слайд 18
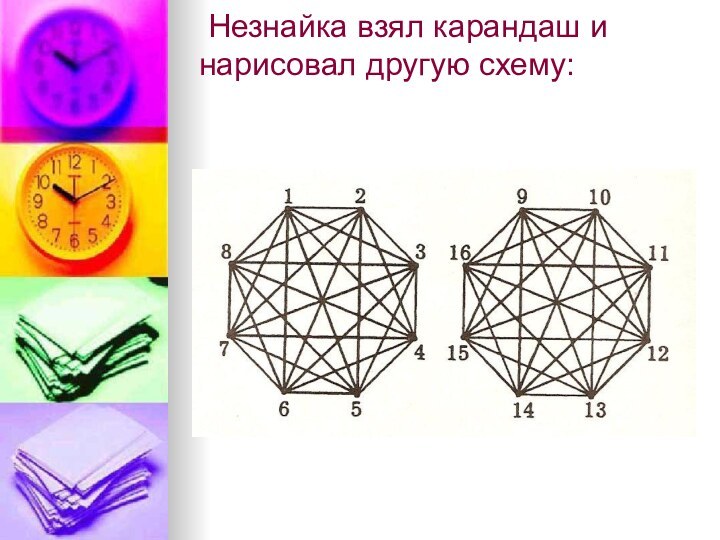
Незнайка взял карандаш и нарисовал другую
схему:
Слайд 19
-Мы разобьем всех игроков на две группы
по восемь малышей в группе. В группах будет играть
каждый с каждым. По два победителя из каждой группы образуют команду. Так будет справедливее.
- А как будем играть с малышками?
- Они предлагают, чтобы каждый из нашей команды сыграл с каждым из их команды. Это можно изобразить таким графом:
Слайд 20
Это двудольный граф. Вершины двудольного графа можно разбить
на две части так, что каждое ребро будет соединять
вершины разных долей. А если каждая вершина одной доли будет соединена с каждой вершиной второй доли, как в этом графе, то получается полный двудольный граф.
Слайд 21
Выбор маршрута.
Через пять дней малыши собрались в
условном месте. Два отборочных турнира подходили к концу. Хотя
еще не все партии были сыграны, но и победители, и команда уже определились.
Незнайка подошел к Знайке, когда тот сидел на лавочке.
- Послушай, я хочу узнать у тебя кое-что...
- В нашей группе было восемь малышей. Они играли с разной скоростью. Торопыжка все свои партии закончил в первый день и все проиграл. А Сиропчик вообще заболел и не сыграл не одной. Но я заметил, что в каждый момент времени обязательно были хотя бы два игрока, которые сыграли одинаковое число партий. Это всегда так?
-Конечно, - ответил Знайка.- Я тебе сейчас все объясню, только ты наверно хотел сказать что Торопыжка сыграл все партии кроме партий с Сиропчиком?
-Да, я сказал неточно.
-Давай нарисуем граф встреч. Вершины графа – это игроки, а если два игрока сыграли партию, то соединим их вершины ребром.
Слайд 22
- Наибольшее количество партий, которое может сыграть
каждый игрок – семь. А для того, чтобы все
игроки сыграли различное количество партий, один игрок должен сыграть семь партий, второй – шесть, третий – пять, четвертый – четыре, пятый – три, шестой – две, седьмой – одну, а восьмой не должен играть вообще. Других вариантов нет.
- Не существует графа, с восемью вершинами, у которого все вершины имеют различные степени.
- Таким образом мы доказали теорему:
В любом графе хотя бы две вершины имеют одинаковую степень
Слайд 23
Пока Знайка и Незнайка разговаривали, к ним подошли
другие малыши.
- Команда для встречи с малышками определилась,
пора определить чемпиона нашего города.- Объявил Знайка.
- А у меня есть предложение: давайте пойдем в поход, а потом разыграем кубок.- Предложил Пулька.
- Давайте, чтобы было удобно, переберем все маршруты, а потом выберем из них лучший!
- Маршрутов не много, - сказал Знайка- Если договориться идти только по тем дорогам которые приближают нас к Зеленому городу, то число маршрутов легко сосчитать. Давайте нарисуем граф дорог. Вершинами этого графа будут города и перекрестки дорог, а ребрами – дороги, соединяющие эти точки.
Слайд 25
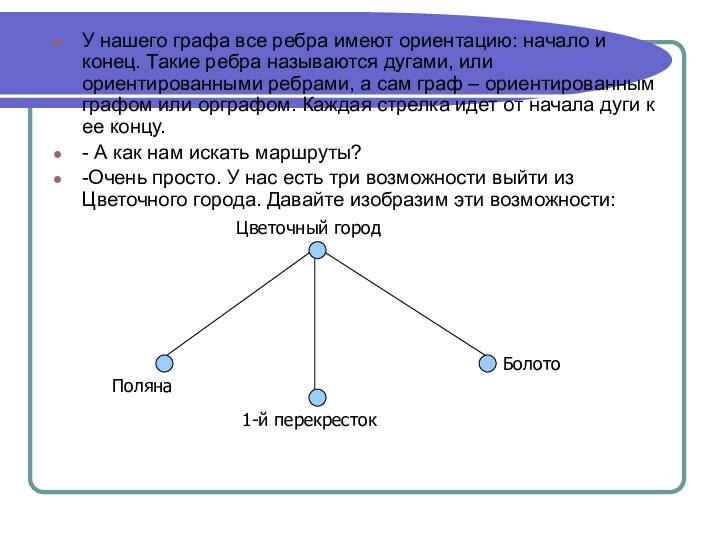
У нашего графа все ребра имеют ориентацию: начало
и конец. Такие ребра называются дугами, или ориентированными ребрами,
а сам граф – ориентированным графом или орграфом. Каждая стрелка идет от начала дуги к ее концу.
- А как нам искать маршруты?
-Очень просто. У нас есть три возможности выйти из Цветочного города. Давайте изобразим эти возможности:
Цветочный город
Болото
1-й перекресток
Поляна
Слайд 26
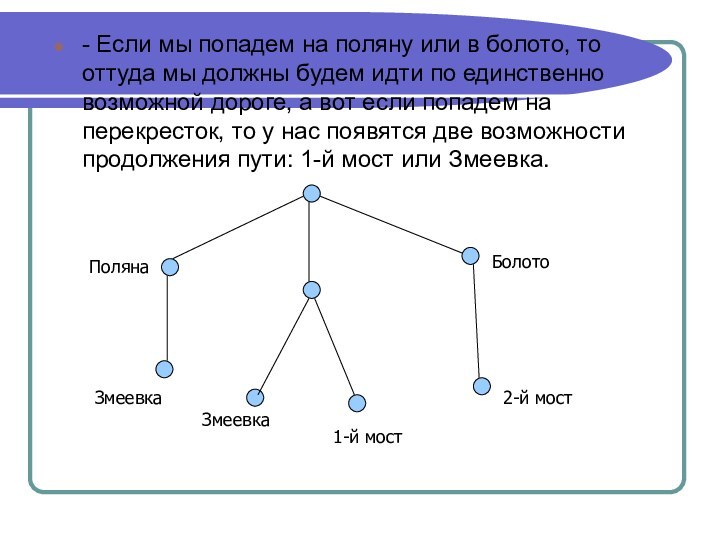
- Если мы попадем на поляну или в
болото, то оттуда мы должны будем идти по единственно
возможной дороге, а вот если попадем на перекресток, то у нас появятся две возможности продолжения пути: 1-й мост или Змеевка.
Болото
2-й мост
1-й мост
Змеевка
Змеевка
Поляна
Слайд 27
- Мы видим, что существуют четыре маршрута,
которые начинаются в Цветочном городе и содержат ровно две
дуги.
- Сейчас мы не учитываем длины дорог, нас интересует только количество разных путей, возразил Знайка.- От первого моста у нас три возможности продолжить путь. От Змеевки – две...
- От второго моста приходим в Зеленый город! Конец пути!
А Знайка нарисовал все возможные продолжения:
Слайд 28
Это корневое дерево. Та вершина которая вверху,
- корень. А то, что дерево растет вниз –
не беда. Мы же говорили . Что не имеет значения, как рисовать граф. Давайте нарисуем остальные варианты маршрутов.
Слайд 29
- Используя построенное дерево, можно найти все
маршруты из Цветочного города в Зеленый. Наше дерево имеет
тринадцать листьев. Значит у нас тринадцать различных маршрутов. Переходя по ребрам дерева от корня к какому-нибудь листу, мы получаем маршрут, соединяющий наши города.