Слайд 2
Unit 1-2
Data Classification
Слайд 3
Types of Data
When doing a study, it is
important to know the kind of data involved. The
nature of the data you are working determines the amount of information contained in the data and indicates the most appropriate data summarization and statistical analysis. In this section, you will learn how to classify data by type and by level of measurement. Data sets can consist of two types of data:
Qualitative Data: consists of attributes, labels or nonnumerical entries. (statistical analysis is fairly limited)
Quantitative Data: consists of numerical measurements or counts.
Слайд 4
Example1
The base prices of several vehicles are shown
in the Table to the left. Which data are
qualitative and which are quantitative? Explain your reasoning.
Слайд 5
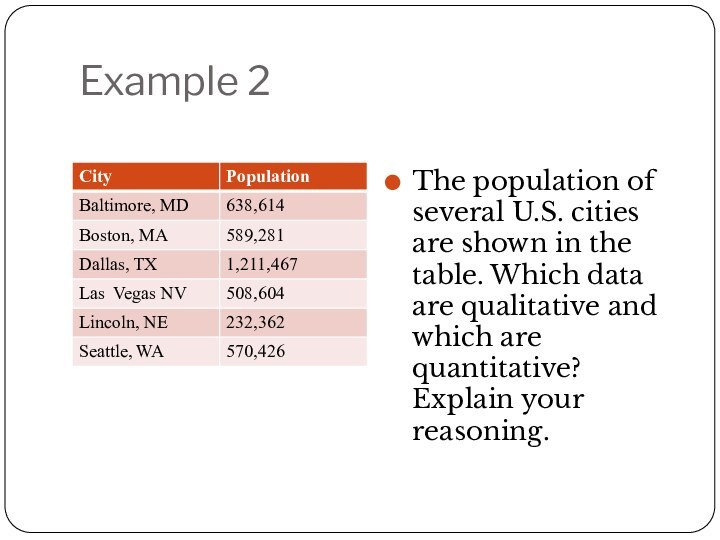
Example 2
The population of several U.S. cities are
shown in the table. Which data are qualitative and
which are quantitative? Explain your reasoning.
Слайд 6
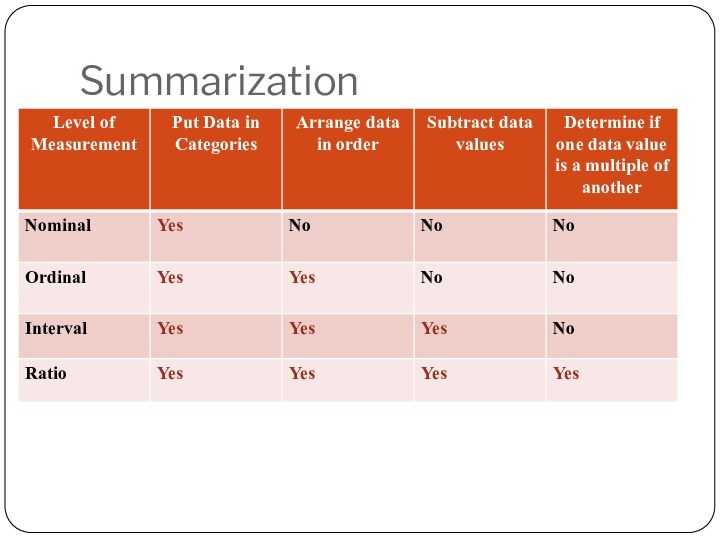
Levels of Measurement
Another characteristic of data is it’s

level of measurement. The level of measurement determines which
statistical calculations are meaningful. The four levels of measurement, in order from lowest to highest, are nominal, ordinal, interval, and ratio.
Data at the nominal level of measurement are qualitative only. Data at this level are categorized using names, labels or qualities. No mathematical computations can be made at this level.
Data at the ordinal level of measurement are qualitative or quantitative. Data at this level can be arranged in order, but differences between data entries are not meaningful.
Data at the interval level of measurement are quantitative. The data can be ordered, and you can calculate meaningful differences between data entries. At the interval level, a zero entry simply represents a position on a scale; the entry is not an inherent zero. (implies “none”)
Data at the ratio level of measurement are similar to data at the interval level, with the added property that a zero entry is an inherent zero. A ratio of two data values can be formed so one data value can be expressed as a multiple of another.
Слайд 7
Inherent Zero
An inherent zero is a zero that
implies “none”. For instance, the amount of money you
have in a savings account could be zero dollars. In this case, the zero represents no money; it is an inherent zero. On the other hand, a temperature of 0˚ C does not represent a condition in which no heat is present. The 0˚ C temperature is simply a position on the Celsius scale. It is NOT an inherent zero.
An easy way to distinguish between the interval and ratio level is to determine whether the expression ”twice as much” has any meaning in the context of the data. For example $2 is twice as much as $1, so these data are at the ratio level. On the other hand, 2˚ C is not twice as warm as 1˚ C, so these data are at the interval level.
Слайд 8
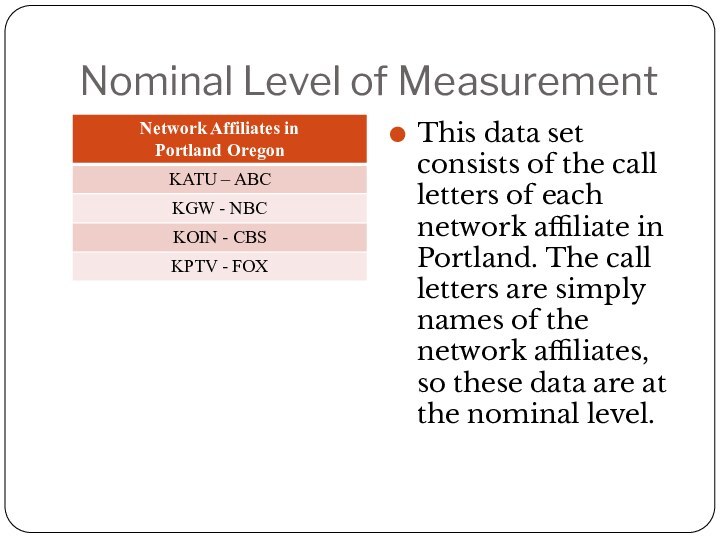
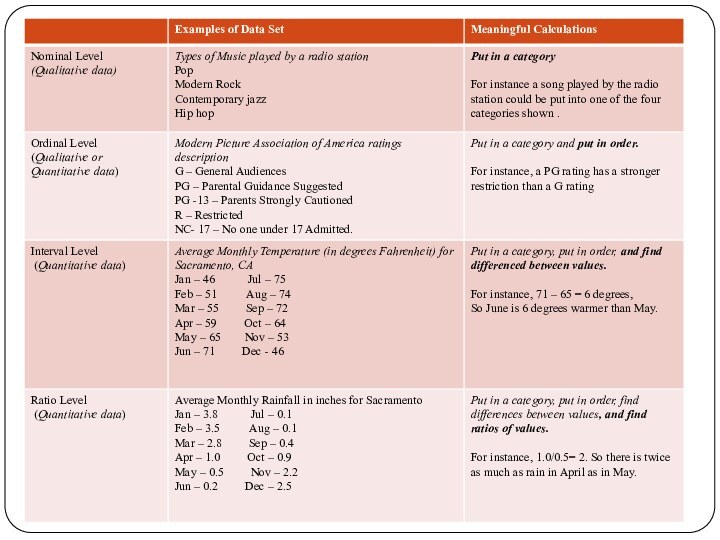
Nominal Level of Measurement
This data set consists of
the call letters of each network affiliate in Portland.
The call letters are simply names of the network affiliates, so these data are at the nominal level.
Слайд 9
Ordinal Level of Measurement
This data set lists the
rank of 5 TV programs. The data consist of
the ranks 1,2, 3, 4, and 5. Because the rankings can be listed in order, these data are at the ordinal level. Note: The difference between the rank of 1 and 5 has no mathematical meaning.
Слайд 10
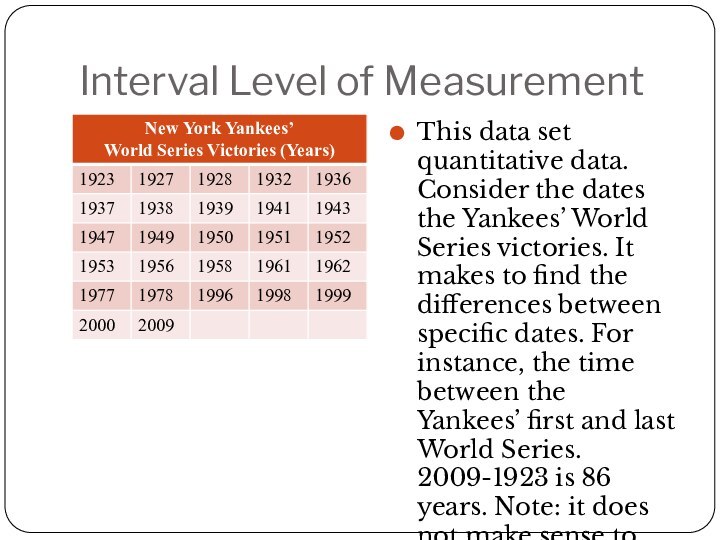
Interval Level of Measurement
This data set quantitative data.
Consider the dates the Yankees’ World Series victories. It
makes to find the differences between specific dates. For instance, the time between the Yankees’ first and last World Series. 2009-1923 is 86 years. Note: it does not make sense to write a ratio using these dates. So, these data are at the interval level.
Слайд 11
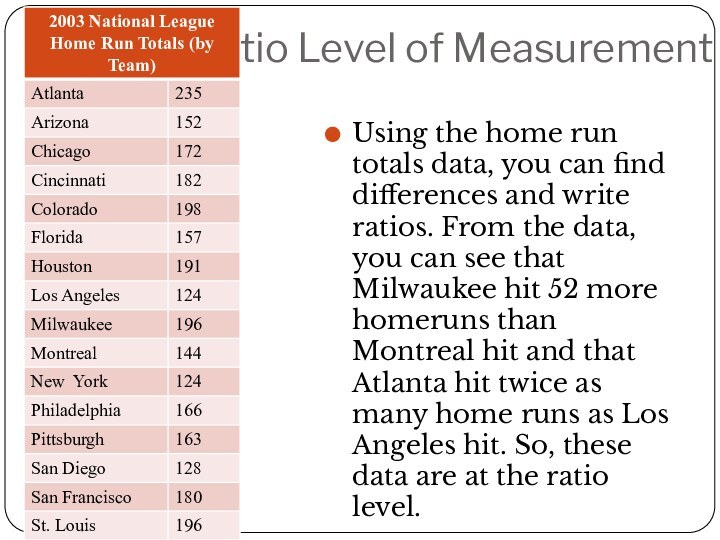
Ratio Level of Measurement
Using the home run totals
data, you can find differences and write ratios. From
the data, you can see that Milwaukee hit 52 more homeruns than Montreal hit and that Atlanta hit twice as many home runs as Los Angeles hit. So, these data are at the ratio level.
Слайд 13
Practice
Consider the following data sets. For each data
set, decide whether the data are at the nominal
level or at the ordinal level.
The final standings for the Northeast Division of the National Hockey league.
A collection of phone numbers.
Слайд 14
Practice
Consider the following data sets. For each data
set, decide whether the data are at the interval
level or at the ratio level.
The body temperature (in degree’s Fahrenheit) of an athlete during an exercise session.
The heart rates ( in beats per minute) of an athlete during an exercise session.