Слайд 2
ВЫВОДЫ:
Плоскость является поверхностью первого порядка. В общем
случае она задается уравнением Ax+By+Cz+D=0,
где A,B,C,D – числа.
2) Коэффициенты A, B, C не обращаются в ноль одновременно, так как с геометрической точки зрения это координаты вектора, перпендикулярного плоскости.
Слайд 3
ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ ПЛОСКОСТИ
Если в уравнении Ax+By+Cz+D =
0 все коэффициенты A,B,C и D отличны от нуля,
то уравнение называют полным; если хотя бы один из коэффициентов равен нулю – неполным.
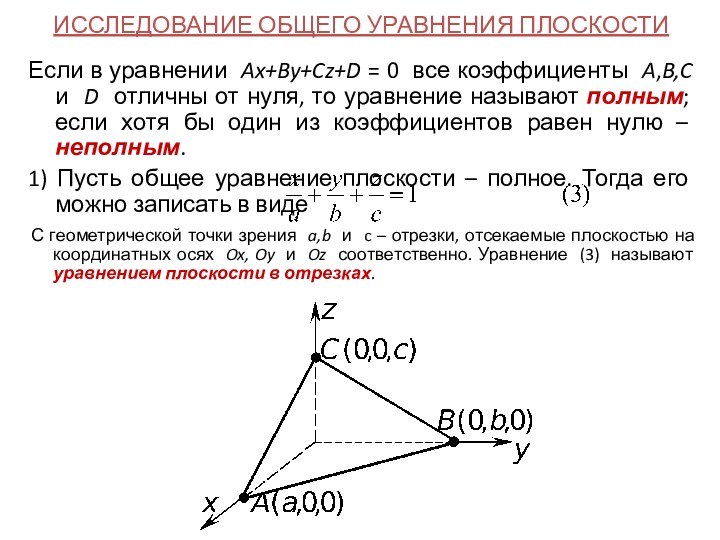
1) Пусть общее уравнение плоскости – полное. Тогда его можно записать в виде
С геометрической точки зрения a,b и c – отрезки, отсекаемые плоскостью на координатных осях Ox, Oy и Oz соответственно. Уравнение (3) называют уравнением плоскости в отрезках.
Слайд 4
2) Пусть в общем уравнении плоскости коэффициенты A,
B и C – ненулевые, а D = 0,
т.е. уравнение плоскости имеет вид
Ax+By +Cz = 0.
Такая плоскость проходит через начало координат O(0;0;0).
ℓ1: By+Cz = 0 (пересечение с плоскостью Oyz)
ℓ2: Ax+By = 0 (пересечение с плоскостью Oxy)
ℓ3: Ax+Сz = 0 (пересечение с плоскостью Oxz)
Слайд 5
а) плоскость отсекает на осях Ox и Oy
отрезки a и b соответственно и параллельна оси Oz;
3)
Пусть в общем уравнении плоскости один из коэффициентов A, B или C – нулевой, а D 0, т.е. уравнение плоскости один из следующих трех видов:
а) Ax+By+D = 0 б) Ax+Cz+D = 0 в) By+Cz+D = 0.
Эти уравнения можно записать соответственно в виде
Слайд 6
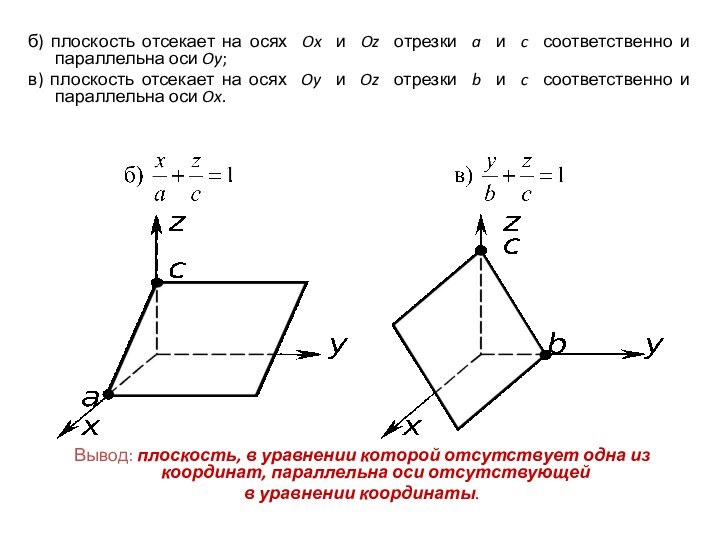
б) плоскость отсекает на осях Ox и Oz
отрезки a и c соответственно и параллельна оси Oy;
в)
плоскость отсекает на осях Oy и Oz отрезки b и c соответственно и параллельна оси Ox.
Вывод: плоскость, в уравнении которой отсутствует одна из координат, параллельна оси отсутствующей
в уравнении координаты.
Слайд 7
4) Пусть в уравнении плоскости (2) два из
трех коэффициентов A, B или C – нулевые, а D
0, т.е. уравнение плоскости имеет вид: а) Ax+D = 0 или б) By+D = 0 или в) Cz+D = 0.
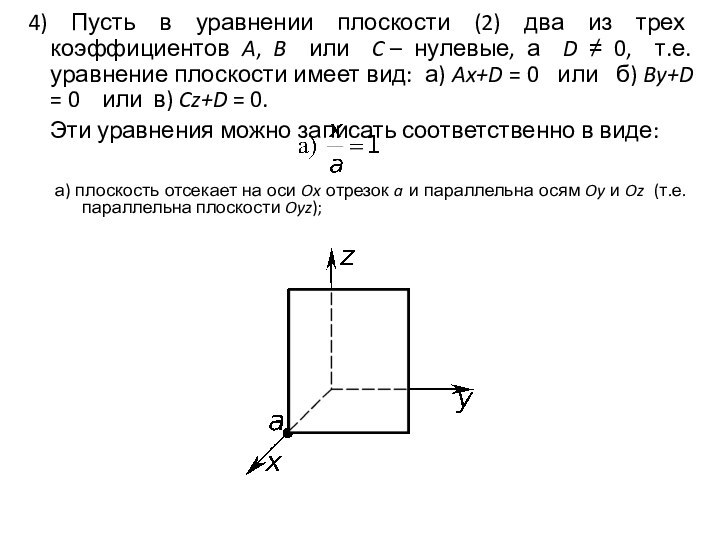
Эти уравнения можно записать соответственно в виде:
а) плоскость отсекает на оси Ox отрезок a и параллельна осям Oy и Oz (т.е. параллельна плоскости Oyz);
Слайд 8
б) плоскость отсекает на Oy отрезок b и
параллельна осям Ox и Oz (т.е. параллельна плоскости Oxz);
в)
плоскость отсекает на Oz отрезок c и параллельна осям Ox и Oy (т.е. параллельна плоскости Oxy).
Вывод: плоскость, в уравнении которой отсутствуют две координаты, параллельна координатной плоскости, проходящей через оси отсутствующих в уравнении координат.
Слайд 9
5) Пусть в общем уравнении плоскости (2) D
= 0 и один из коэффициентов A, B или
C тоже нулевой, т.е. уравнение плоскости имеет вид:
а) Ax+By = 0 или б) Ax+Cz = 0 или в) By+Cz = 0.
Вывод: Плоскость проходит через начало координат и ось отсутствующей в уравнении координаты.
Слайд 10
6) Пусть в общем уравнении плоскости (2) три
коэффициента равны нулю, т.е. уравнение плоскости имеет вид
а)
Ax = 0 или б) By = 0 или в) Cz = 0.
Эти уравнения можно записать соответственно в виде:
а) x = 0 – уравнение координатной плоскости Oyz;
б) y = 0 – уравнение координатной плоскости Oxz,
в) z = 0 – уравнение координатной плоскости Oxy.
Слайд 11
2. Другие формы записи уравнения плоскости
Уравнение плоскости, проходящей
через точку
параллельно двум неколлинеарным векторам
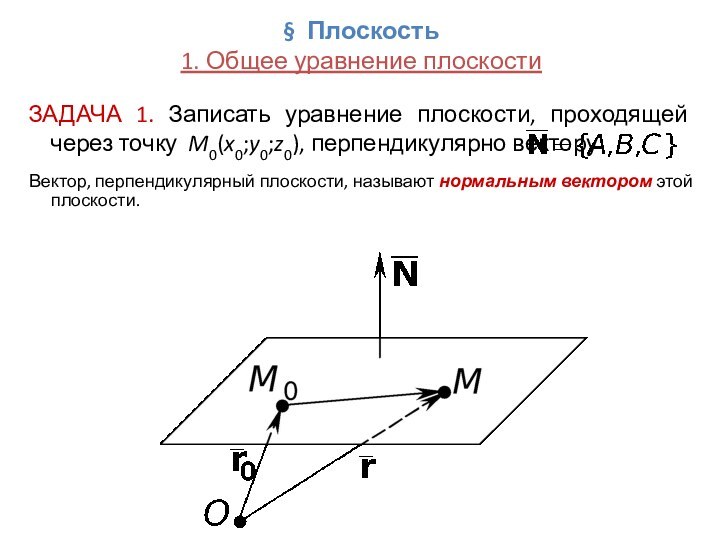
ЗАДАЧА
2. Записать уравнение плоскости, проходящей через точку M0(x0;y0;z0), параллельно неколлинеарным векторам
Другие формы записи:
Уравнение плоскости, проходящей через точку параллельно двум неколлинеарным векторам;
Уравнение плоскости, проходящей через три точки;
Слайд 13
Уравнение плоскости, проходящей через три точки, не
лежащие на одной прямой – частный случай уравнения
(4)
Пусть плоскость проходит через три точки M1(x1;y1;z1), M2(x2;y2;z2) и M3(x3;y3;z3), не лежащие на одной прямой.
Слайд 14
3. Взаимное расположение плоскостей
В пространстве две плоскости
могут:
а) быть параллельны, б) пересекаться.
Пусть плоскости λ1 и λ2 заданы общими уравнениями:
λ1: A1x + B1y + C1z + D1 = 0
λ2: A2x + B2y + C2z + D2 = 0
Тогда:
Слайд 15
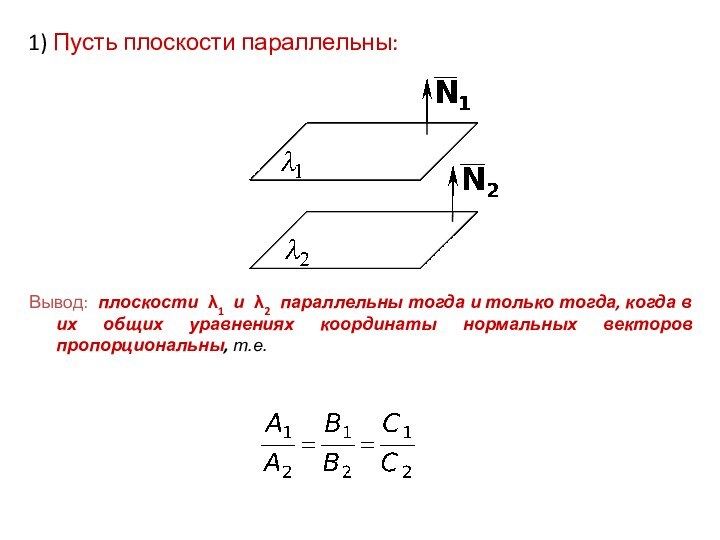
1) Пусть плоскости параллельны:
Вывод: плоскости λ1 и λ2
параллельны тогда и только тогда, когда в их общих
уравнениях координаты нормальных векторов пропорциональны, т.е.
Слайд 16
2) Пусть плоскости пересекаются
где знак плюс берется, когда
надо найти величину острого угла, а знак минус –
когда надо найти величину тупого угла.
Слайд 17
Частный случай – плоскости перпендикулярны, т.е.
(критерий перпендикулярности плоскостей,
заданных общими уравнениями)
Слайд 18
4. Расстояние от точки до плоскости
ЗАДАЧА 3. Пусть
плоскость λ задана общим уравнением
Ax + By +
Cz + D = 0 ,
M0(x0;y0;z0) – точка, не принадлежащая плоскости λ .
Найти расстояние от точки M0 до плоскости λ .
Слайд 19
§ Прямая в пространстве
1. Уравнения прямой в пространстве
Пусть A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 – уравнения любых двух
различных плоскостей, содержащих прямую ℓ . Тогда координаты любой точки прямой ℓ удовлетворяют одновременно обоим уравнениям, т.е. являются решениями системы
Систему (1) называют общими уравнениями прямой в пространстве.
Слайд 20
Другие формы записи уравнений прямой в пространстве –
ПАРАМЕТРИЧЕСКИЕ и КАНОНИЧЕСКИЕ уравнения.
ЗАДАЧА 1. Записать уравнение прямой в
пространстве, проходящей через точку M0(x0;y0;z0) , параллельно вектору
Вектор, параллельный прямой в пространстве, называют направляющим вектором этой прямой.
Слайд 21
называют параметрическими уравнениями прямой в пространстве (в векторной
и координатной форме соответственно).
Слайд 22
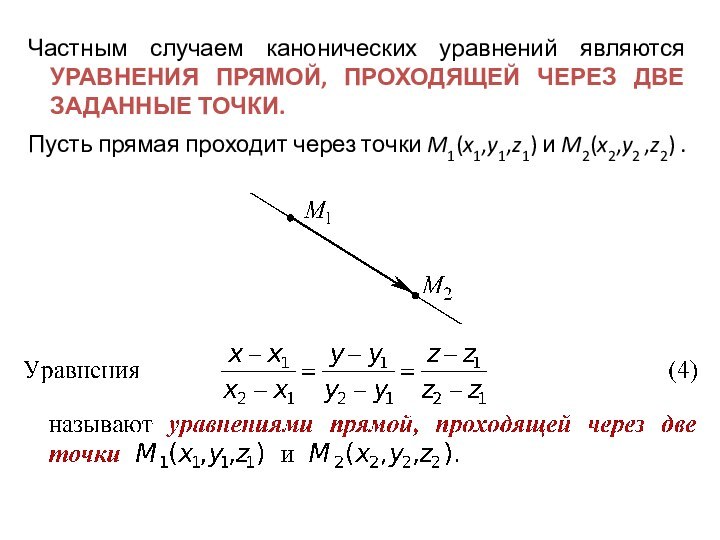
Частным случаем канонических уравнений являются УРАВНЕНИЯ ПРЯМОЙ, ПРОХОДЯЩЕЙ
ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ.
Пусть прямая проходит через точки
M1(x1,y1,z1) и M2(x2,y2 ,z2) .
Слайд 23
2. Переход от общих уравнений прямой к каноническим
Пусть прямая ℓ задана общими уравнениями:
Чтобы записать канонические
(параметрические) уравнения этой прямой, необходимо найти ее направляющий вектор и координаты какой-нибудь точки M0(x0;y0;z0) на прямой.
а) Координаты точки M0 – это одно из решений системы (1).
б) Направляющий вектор
Слайд 24
3. Взаимное расположение прямых в пространстве
В пространстве
две прямые могут:
а) быть параллельны,
б) пересекаться, в) скрещиваться.
Пусть прямые ℓ1 и ℓ2 заданы каноническими уравнениями:
1) Пусть прямые ℓ1 и ℓ2 параллельны:
Слайд 25
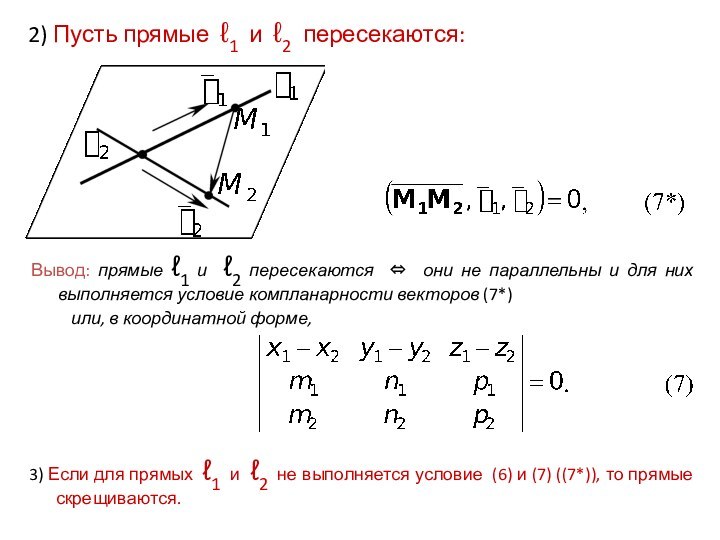
2) Пусть прямые ℓ1 и ℓ2 пересекаются:
Вывод: прямые
ℓ1 и ℓ2 пересекаются они не параллельны и
для них выполняется условие компланарности векторов (7*)
или, в координатной форме,
3) Если для прямых ℓ1 и ℓ2 не выполняется условие (6) и (7) ((7*)), то прямые скрещиваются.
Слайд 26
4. Задачи, связанные с возможным взаимным расположением прямых
Возможное
расположение прямых в пространстве приводит к следующим задачам:
1) параллельные
прямые расстояние между прямыми
(т.е. расстояние от точки до прямой)?
2) пересекающиеся прямые а) угол между прямыми?
б) точка пересечения прямых?
3) скрещивающиеся прямые а) угол между прямыми?
б) расстояние между прямыми?
Слайд 27
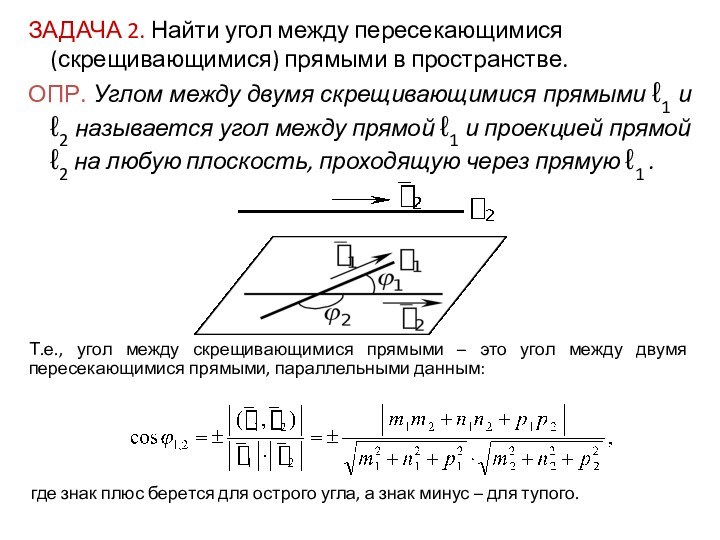
ЗАДАЧА 2. Найти угол между пересекающимися (скрещивающимися) прямыми
в пространстве.
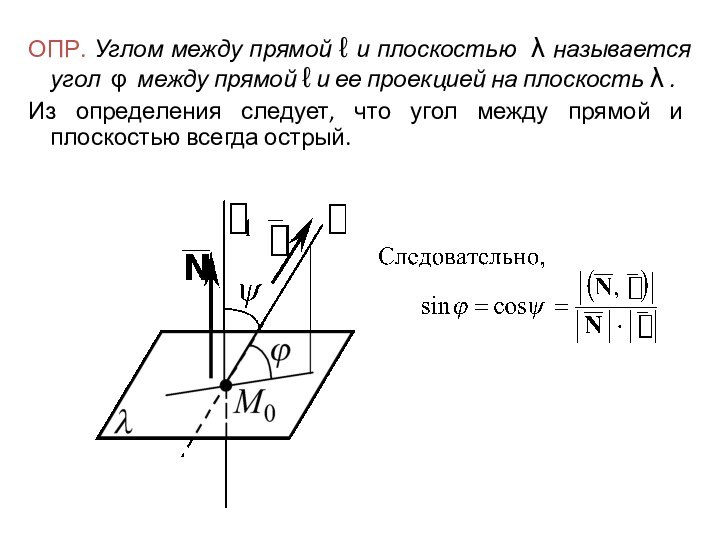
ОПР. Углом между двумя скрещивающимися прямыми ℓ1 и
ℓ2 называется угол между прямой ℓ1 и проекцией прямой ℓ2 на любую плоскость, проходящую через прямую ℓ1 .
Т.е., угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, параллельными данным:
где знак плюс берется для острого угла, а знак минус – для тупого.
Слайд 28
ЗАДАЧА 3. Найти расстояние от точки до прямой
в пространстве.
Слайд 29
ЗАДАЧА 4. Найти расстояние между скрещивающимися прямыми.
ОПР. Расстоянием между двумя скрещивающимися прямыми называется длина их
общего перпендикуляра.
где Ax + By + Cz + D = 0 – общее уравнение плоскости λ ,
M2(x2; y2; z2) – любая точка на прямой ℓ2 .
Слайд 30
Тогда d – высота пирамиды (параллелепипеда), опущенная
из точки M2.
Следовательно:
Слайд 31
ЗАДАЧА 5. Найти точку пересечения прямых.
Пусть M0(x0;y0;z0)
– точка пересечения прямых. Тогда (x0;y0;z0) – решение системы
уравнений
Слайд 32
5. Взаимное расположение прямой и плоскости в пространстве
Пусть в пространстве заданы плоскость λ и прямая ℓ
. Они могут 1) быть параллельны;
2) прямая может лежать в плоскости;
3) прямая и плоскость могут пересекаться в одной точке.
Слайд 33
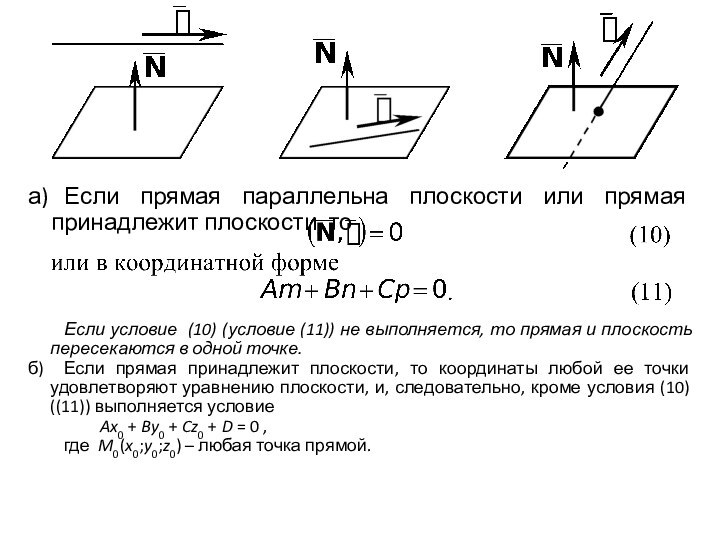
а) Если прямая параллельна плоскости или прямая принадлежит плоскости,
то
Если условие (10) (условие (11)) не выполняется, то
прямая и плоскость пересекаются в одной точке.
б) Если прямая принадлежит плоскости, то координаты любой ее точки удовлетворяют уравнению плоскости, и, следовательно, кроме условия (10) ((11)) выполняется условие
Ax0 + By0 + Cz0 + D = 0 ,
где M0(x0;y0;z0) – любая точка прямой.
Слайд 34
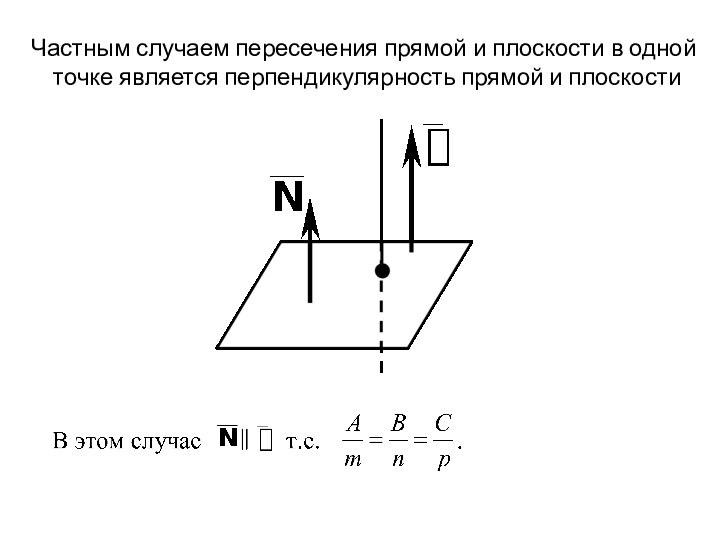
Частным случаем пересечения прямой и плоскости в одной
точке является перпендикулярность прямой и плоскости