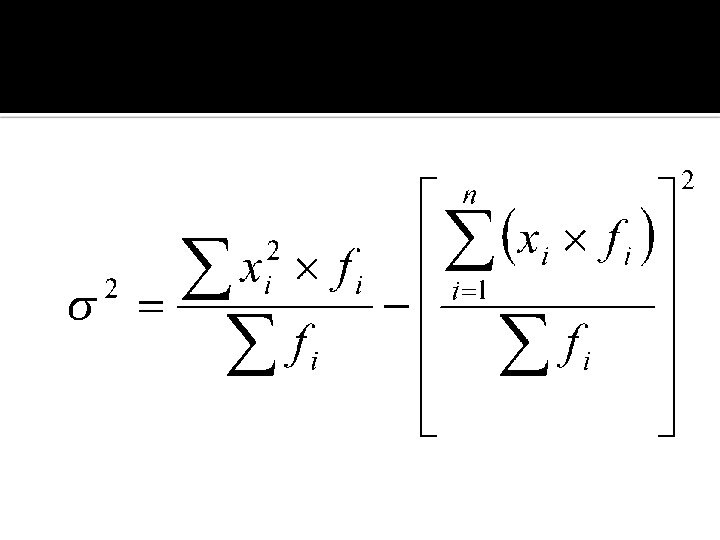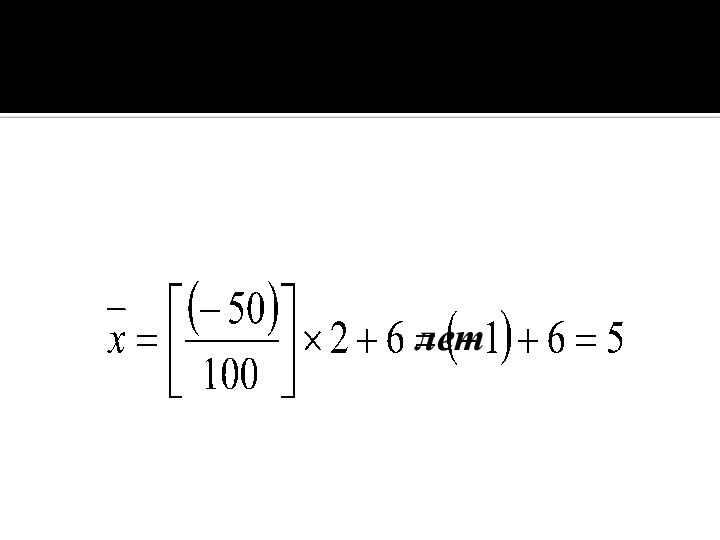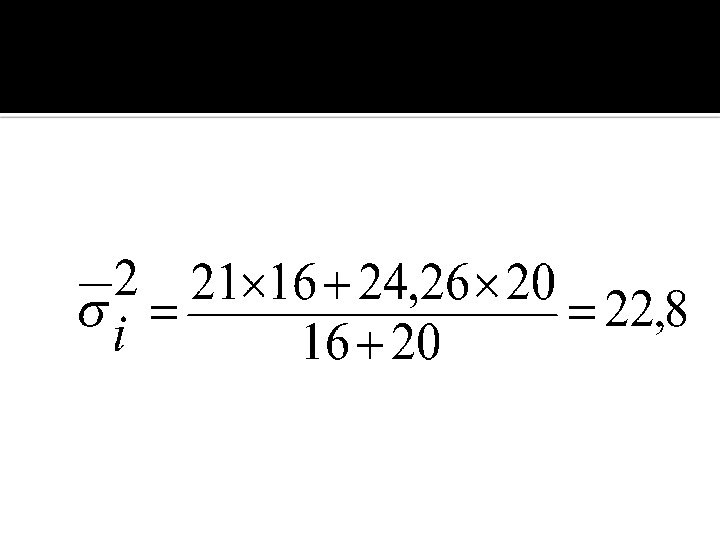Слайд 2
1. Понятие, причины и показатели вариации
Вариация –
различие значений какого-либо признака у разных единиц совокупности за
один и тот же промежуток времени.
Причиной возникновения вариации являются различные условия существования разных единиц совокупности.
Слайд 3
Определение вариации необходимо при выборочном наблюдении, статистическом моделировании,
проведении экспертных опросов.
По степени вариации судят об однородности совокупности,
устойчивости значений признака, типичности средней, о взаимосвязи между признаками.
Слайд 4
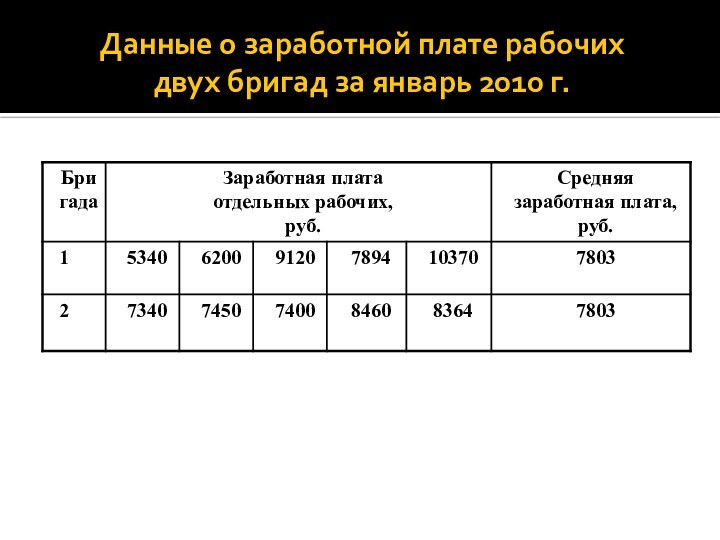
Данные о заработной плате рабочих
двух бригад за
январь 2010 г.
Слайд 5
При оценке социально-экономических явлений нельзя ограничиваться расчетом только
средней величины, надо знать её устойчивость и масштабы отклонения
от средней.
Слайд 6
Для измерения степени колеблемости отдельных значений признака от
средней исчисляются абсолютные и относительные показатели вариации.
Абсолютные показатели
вариации:
размах вариации;
среднее линейное отклонение;
дисперсия;
среднее квадратическое отклонение.
Относительные показатели вариации:
коэффициент вариации;
коэффициент осцилляции и др.
Слайд 7
Размах вариации (R) является наиболее простым способом измерения
колеблемости и рассчитывается как разность между максимальным и минимальным
значениями признака:
R = хmах – хmin .
Слайд 8
Среднее линейное отклонение ( ) рассчитывается
как средняя из модулей отклонений вариантов признака от средней.
Для ранжированного ряда:
Слайд 9
Для вариационного ряда распределения:
где хi – индивидуальные значения
признака;
– среднее значение признака;
n – объем совокупности;
f – частота значений признака.
Слайд 10
Дисперсия (2) – это средняя арифметическая квадратов отклонений
отдельных значений признака от их средней арифметической.
Дисперсия является
основным показателем вариации.
Слайд 11
Дисперсия для ранжированного ряда рассчитывается по формуле:
Слайд 12
Для вариационного ряда распределения:
Слайд 13
Среднее квадратическое отклонение () - представляет собой квадратный
корень из среднего квадрата отклонений отдельных значений признака от
их средней, т. е. корень квадратный из дисперсии.
Слайд 14
Для ранжированного ряда показатель рассчитывается по формуле:
Слайд 15
Для вариационного ряда распределения:
Слайд 16
Коэффициент вариации (γ) является относительным показателем вариации и
представляет собой процентное отношение среднего квадратического отклонения к средней
арифметической:
Слайд 17
По коэффициенту вариации судят о степени вариации признака,
об однородности совокупности.
Совокупность считается однородной, а среднее значение признака
– типичным для совокупности, если коэффициент вариации не превышает 33-35 %.
Слайд 18
Пример 1: Данные о распределении работников банка по
стажу работы:
Слайд 19
Определить:
Средний стаж работников
Размах вариации
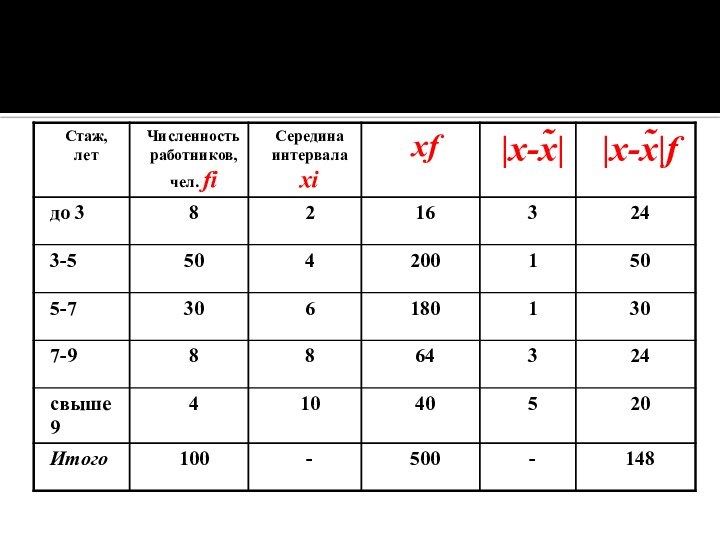
Среднее линейное отклонение
Дисперсию
Среднее квадратическое отклонение
Коэффициент
вариации
Слайд 20
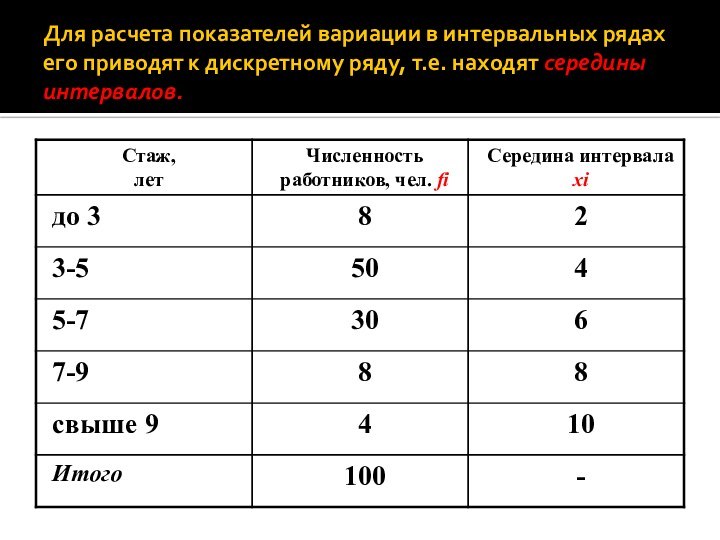
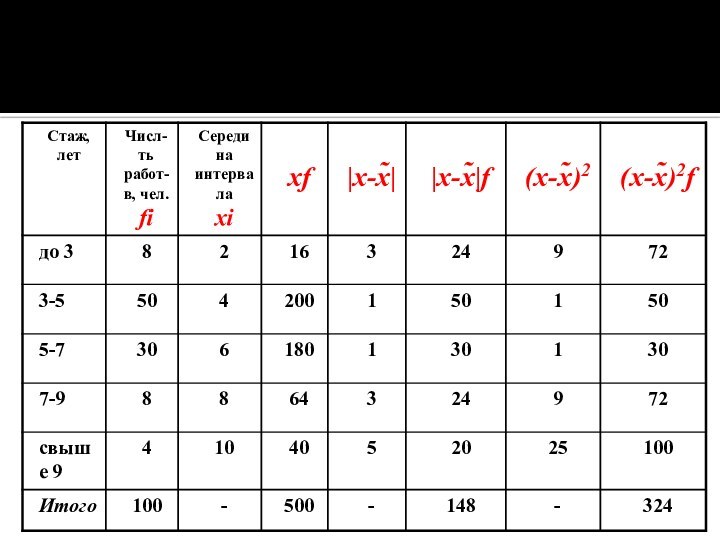
Для расчета показателей вариации в интервальных рядах его
приводят к дискретному ряду, т.е. находят середины интервалов.
Слайд 22
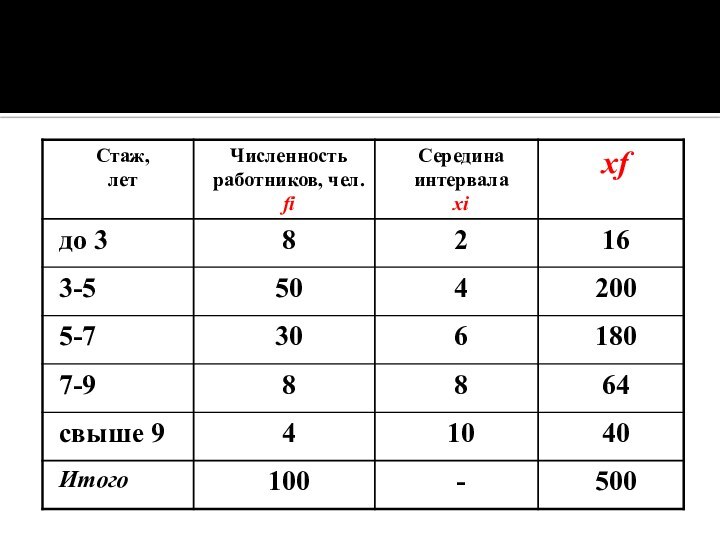
При определении среднего стажа работников используем формулу средней
арифметической взвешенной.
Слайд 23
Размах вариации определяем по формуле:
R = хмах –хмin
= 10 – 2 = 8 (лет).
Слайд 28
Среднее квадратическое отклонение:
лет
Слайд 30
2. Расчеты дисперсии сокращенными способами
Дисперсия сокращенным способом определяется
по формуле:
где k – величина интервала; А – условный
нуль, в качестве которого удобно использовать середину интервала с наибольшей частотой.
Слайд 31
Формула расчёта дисперсии
по «методу моментов»:
2 = k2
(m2 – m12),
Слайд 34
В случае, когда А = 0 и, следовательно,
не вычисляются отклонения, формула расчета дисперсии «от условного нуля»
принимает вид:
2 = х2 –
Слайд 36
Пример 2: По данным о стаже работников банка
определить дисперсию по способу «от условного нуля» и «методом
моментов»:
Слайд 38
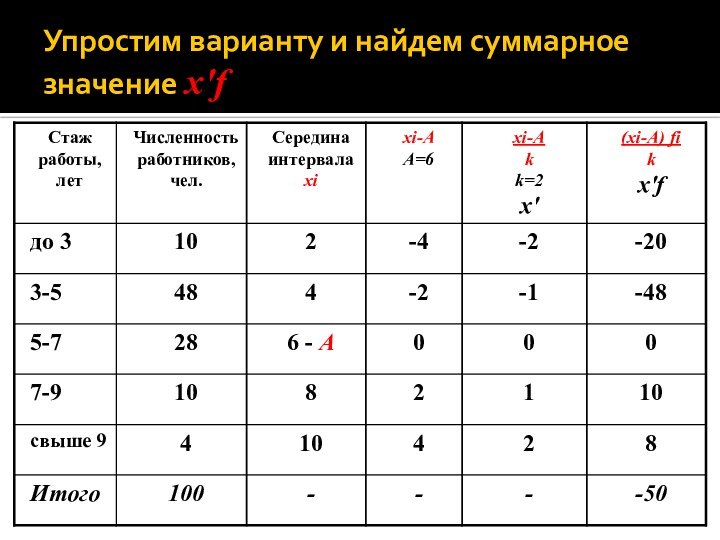
Упростим варианту и найдем суммарное значение x'f
Слайд 40
2. Дисперсия по способу расчёта «от условного нуля»:
Слайд 41
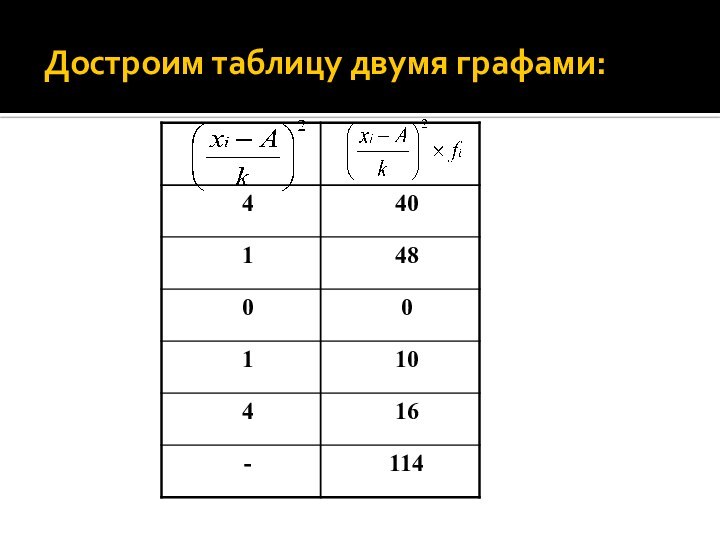
Достроим таблицу двумя графами:
Слайд 42
Рассчитаем дисперсию «от условного нуля»:
Слайд 43
По способу "моментов" получаем:
2 = k2 (m2
– m12),
Слайд 44
3. Виды дисперсий. Правило сложений дисперсий
Если совокупность разбивается
на группы по изучаемому признаку, то для этой совокупности
вычисляются дисперсии:
общая (σ²);
внутригрупповые (частные) (σ²і);
средняя из внутригрупповых ( );
межгрупповая (δ²).
Слайд 45
«правило сложения дисперсий»
Общая дисперсия равна
сумме средней из
внутригрупповых
и межгрупповой дисперсий:
Слайд 46
Внутригрупповая дисперсия отражает случайную вариацию, происходящую
под влиянием
неучтённых факторов.
Слайд 47
Средняя из внутригрупповых дисперсий:
Слайд 48
Межгрупповая дисперсия является объясненной дисперсией.
Она вызывается влиянием фактора,
положенного в основу группировки.
Слайд 49
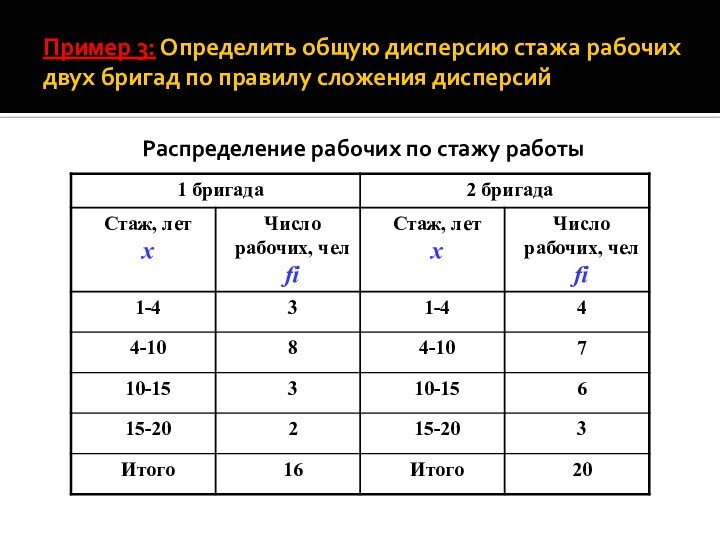
Пример 3: Определить общую дисперсию стажа рабочих двух
бригад по правилу сложения дисперсий
Распределение рабочих по стажу работы
Слайд 50
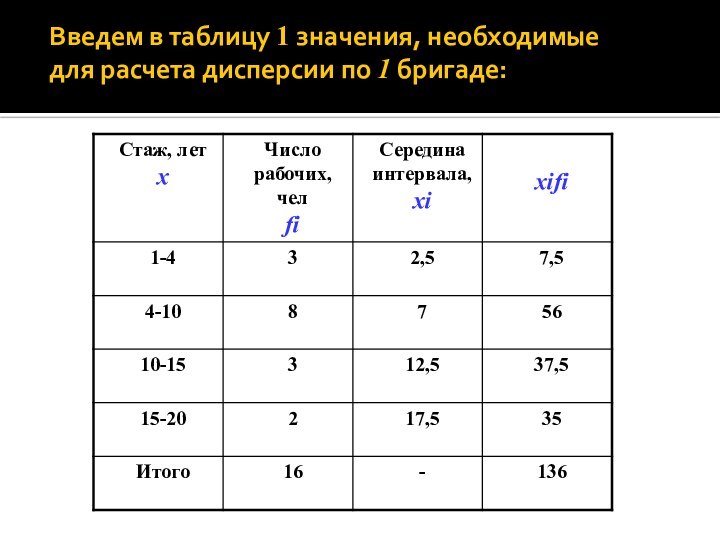
Введем в таблицу 1 значения, необходимые
для расчета
дисперсии по 1 бригаде:
Слайд 51
Средний стаж у рабочих 1 бригады:
лет
Слайд 52
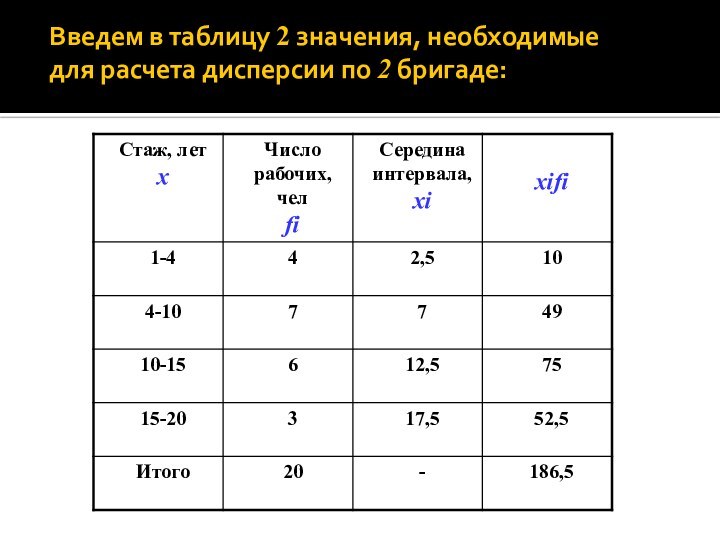
Введем в таблицу 2 значения, необходимые
для расчета
дисперсии по 2 бригаде:
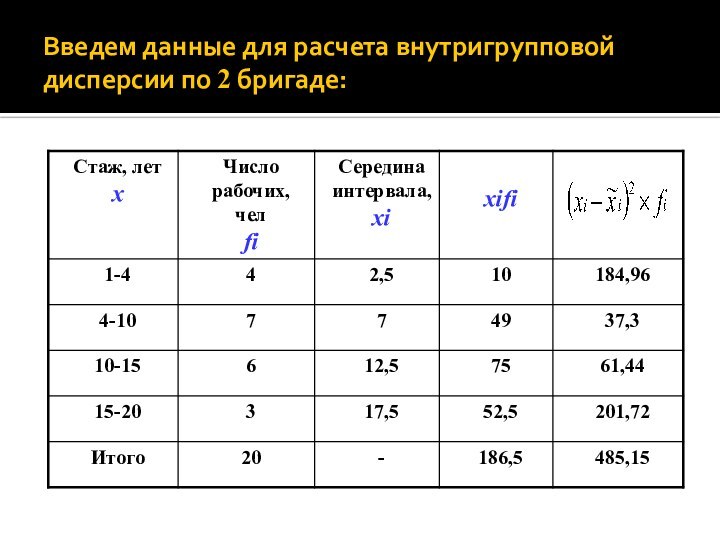
Слайд 53
Средний стаж у рабочих 2 бригады:
лет
Слайд 54
Введем данные для расчета внутригрупповой дисперсии по 1
бригаде:
Слайд 55
Внутригрупповая дисперсия для рабочих:
Слайд 56
Внутригрупповая дисперсия по 1 бригаде:
Слайд 57
Введем данные для расчета внутригрупповой дисперсии по 2
бригаде:
Слайд 58
Внутригрупповая дисперсия по 2 бригаде:
Слайд 59
Средняя из внутригрупповых дисперсий:
Слайд 61
Для межгрупповой дисперсии δ2 рассчитаем средний стаж для
рабочих двух бригад вместе:
Слайд 62
Определим межгрупповую дисперсию δ2:
Слайд 64
Используя правило сложений дисперсий, определяем общую дисперсию:
σ2 =
22,8 + 0,16 = 22,96.
Слайд 65
Для характеристики оценки тесноты связи между факторным и
результативным признаками используются показатели:
эмпирического коэффициента детерминации (η2);
эмпирического корреляционного
отношения (η).
Слайд 66
Эмпирический коэффициент детерминации :
Слайд 67
Если η2 = 100 %, то вариация результативного
признака целиком определяется изменением факторного;
если η2 = 0,
то группировочный фактор не влияет на изменение результативного;
если 0< η2 <100, то на измерение результативного влияет не только группировочный, но и другие признаки.
Слайд 68
Эмпирическое корреляционное отношение :
Слайд 69
Значения эмпирического корреляционного отношения находятся в пределах от
0 до 1 и характеризуют тесноту связи между факторным
и результативным признаком:
0,0-0,3 –связь слабая
0,3-0,5 – умеренная
0,5-0,7 – заметная
0,7-0,9 – высокая
0,9-0,99 – очень высокая.
Слайд 70
4. Дисперсия альтернативного признака
Существуют качественные признаки, которые имеют
лишь два противоположных значения: имеется этот признак или нет
(наличие высшего образования, наличие стипендии, бракованность продукции и т. д.).
Слайд 71
Таким качественным признакам можно придать условные
количественные значения:
1
– наличие признака;
0 – отсутствие признака
Слайд 72
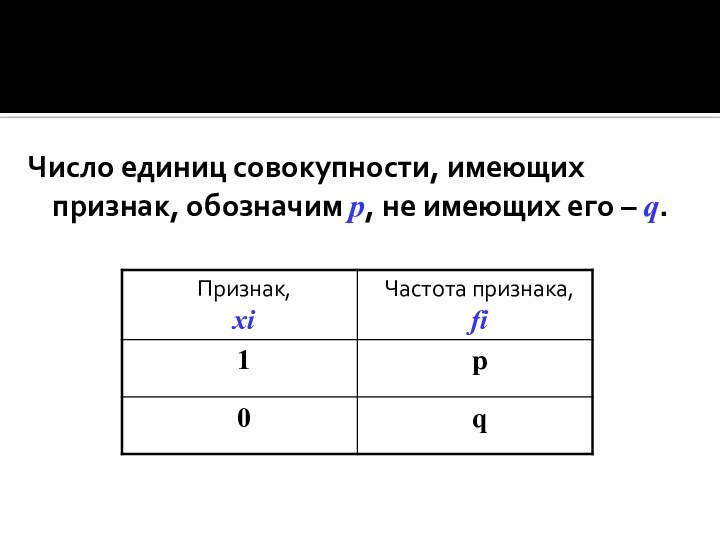
Число единиц совокупности, имеющих признак, обозначим p, не
имеющих его – q.
Слайд 73
Cреднее значение признака во всей совокупности (по формуле
средней арифметической взвешенной) будет равно:
Слайд 74
Находим дисперсию альтернативного признака (по обычной формуле):
Слайд 75
Значение дисперсии альтернативного признака не может превышать 0,25,
так как:
0,1 х 0,9=0,09
0,2 х 0,8=0,16
0,3 х 0,7=0,21
0,4 х
0,6=0,24
0,5 х 0,5=0,25.