- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему дипломной работы Методика изучения правильных многогранников в школьном курсе математики
Содержание
- 2. Цель: рассмотреть определение и основные свойства правильных
- 3. Задачи:- изучить и проанализировать педагогическую, методическую литературу
- 4. Виды правильных многогранников:тетраэдргексаэдр (куб)додекаэдроктаэдрикосаэдр
- 6. Свойства правильного тетраэдра:
- 7. Многогранник называется правильным, если выполняются такие условия:
- 8. ЗАДАЧИ: 1. Задачи на различные определения
- 9. Существует ли сечение куба, являющееся правильным шестиугольником?Решение: Существует.
- 10. «Многогранники: виды задач и методы их решения»
- 11. Темы:- Выпуклые многогранники- Построение сечений многогранников- Вычисление
- 12. - Природные многогранники (кристаллы).- Простейшие
- 13. Выводы:При написании работы было изучено множество учебников
- 14. Скачать презентацию
- 15. Похожие презентации
Цель: рассмотреть определение и основные свойства правильных многогранников, методику их изучения; возможность более глубокого изучения темы «Правильные многогранники».



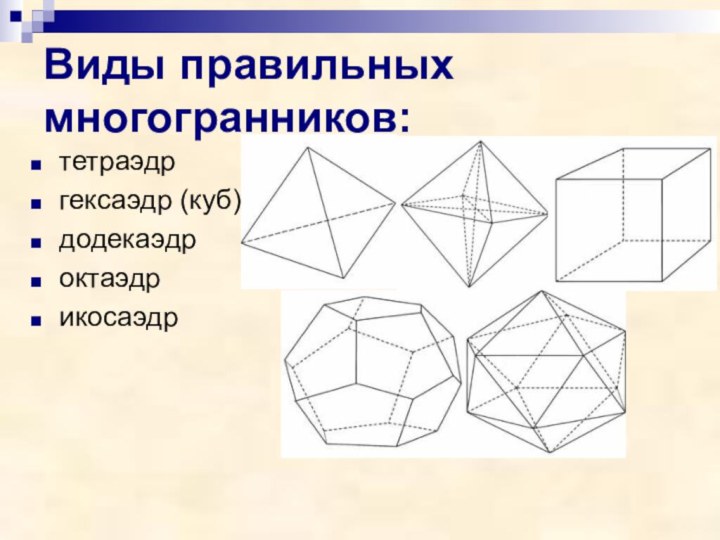
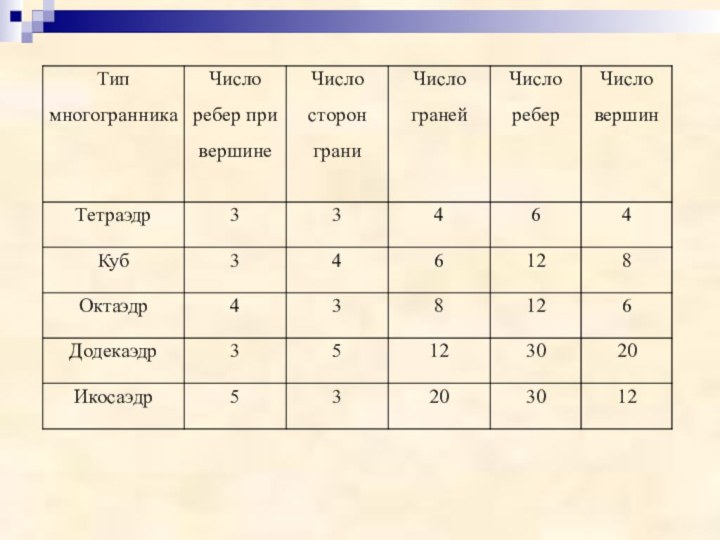









Слайд 3
Задачи:
- изучить и проанализировать педагогическую, методическую литературу по
теме исследования;
- раскрыть теоретические особенности изучения данной темы;
- подобрать
различные задачи по теме «Правильные многогранники» и примерный элективный курс по данной теме.Слайд 7 Многогранник называется правильным, если выполняются такие условия: он
выпуклый; одинаковое количество ребер сходится в каждой из его
вершин; все грани его - правильные многоугольники, равные друг другу; все двугранные углы его равны.Слайд 8 ЗАДАЧИ: 1. Задачи на различные определения правильных многогранников, 2. Задачи
на нахождение элементов правильных многогранников, 3. Задачи на проекции и
сечения правильных многогранников.
Слайд 9
Существует ли сечение куба, являющееся правильным шестиугольником?
Решение:
Существует. Докажем
это:
У куба ABCDA1B1C1D1 существует сечение в виде правильного треугольника
A1C1DМожно построить сечение в виде правильного шестиугольника так: вершины шестиугольника разместить на середине ребер AD, DC, CC1, C1B1, B1A1, A1A.
Этот шестиугольник правильный, так как его стороны параллельны сторонам треугольника A1C1D и в два раза меньше их.
Слайд 10
«Многогранники: виды задач и методы их решения»
Элективный курс
Цель курса: расширить представления учащихся о методах,
приемах, подходах к решению задач по стереометрии в системе подготовки к ЕГЭ по математике.
Слайд 11
Темы:
- Выпуклые многогранники
- Построение сечений многогранников
- Вычисление расстояния
между точками. Вычисление расстояния от точки до прямой. Вычисление
расстояния между прямыми.- Вычисление углов между прямыми, между прямой и плоскостью, между плоскостями
- Площадь поверхности многогранника
- Объем многогранника
- Правильные многогранники. Полуправильные многогранники. Звездчатые многогранники.
Слайд 12
- Природные многогранники (кристаллы).
- Простейшие задачи
на построение сечений куба.
- Простейшие задачи на построение сечений
тетраэдра.- Задачи на нахождение наибольших и наименьших значений площадей и периметров сечений куба и тетраэдра.
- Куб и тетраэдр: вычисление расстояний между точками, от точки до прямой, между прямыми.
- Куб и тетраэдр: вычисление углов между прямыми, межу прямой и плоскостью, между плоскостями.
- Куб и тетраэдр: вычисление площадей и объёмов.
- Нахождение угла между плоскостью сечения и одной из граней многогранника.
- Вычисление объемов многогранников, на которые разбивается данный плоскостью сечения.
- Задачи на нахождение наибольших и наименьших значений площадей и периметров сечений.
Слайд 13
Выводы:
При написании работы было изучено множество учебников и
учебных пособий по геометрии по вопросу исследования правильных многогранников;
Изучение свойств правильных многогранников способствует повышению интереса у учащихся к предмету, развитию пространственных представлений, изобретательности, формированию логического мышления, необходимых практических навыков в моделировании и конструировании пространственных фигур;
Чтобы дать учащимся полное представление о правильных многогранниках, необходимо более глубокое изучение их свойств на дополнительных занятиях.





























