- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Уникурсальные фигуры
Содержание
- 2. К XVIII в. через реку Прегель, протекавшую
- 3. Рассказывают, что однажды один из жителей города
- 4. Этой задачей заинтересовались многие, однако решить её
- 5. Решая задачу о семи мостах, Эйлер поступил
- 6. Эйлер подсчитал число дуг, исходящих из каждой
- 7. Свойства графа:Число нечетных вершин графа всегда четно.
- 8. Поскольку число нечетных вершин графа, соответствующего задаче
- 9. Задача 1Можно ли привязать к гвоздям A,
- 10. Из рисунка видно, что из вершин A,
- 11. Начертим теперь без отрыва карандаша от бумаги
- 12. Подсчитаем теперь число дуг, исходящих из этих
- 13. Фигура (граф), которую можно начертить одним росчерком
- 14. Задача 2В небольшой роще находится заяц. Выскочив
- 15. Будем считать каждое дерево вершиной графа, а
- 16. Задачи и упражнения1. У какой уникурсальной фигуры
- 17. 2. У какой уникурсальной фигуры начальная и
- 18. 3. Какие из фигур, изображенных на рисунке,
- 19. 4. Какие буквы русского алфавита уникурсальны?Б, Г, З, И, Л, М, О, П, Р, С, Я
- 20. 5. Однажды пионеры попросили пионервожатую организовать экскурсию
- 21. 6. Каково наименьшее число росчерков, которыми можно
- 22. Скачать презентацию
- 23. Похожие презентации


















Слайд 3 Рассказывают, что однажды один из жителей города спросил
у своего соседа, сможет ли он пройти по всем
мостам так, чтобы на каждом из них побывать лишь один раз и вернуться к тому месту, откуда начал прогулку.Перед вами план Кёнигсберга. Можете попробовать!
Слайд 4 Этой задачей заинтересовались многие, однако решить её никто
из жителей города так и не смог.
В дальнейшем задача
привлекла внимание разных стран. Решить её удалось в 1736 г. известному швейцарскому математику Леонарду Эйлеру. Причем Эйлер не только решил эту задачу, но и сумел найти общий метод решения аналогичных задач.Слайд 5 Решая задачу о семи мостах, Эйлер поступил следующим
образом. Он изобразил точками B и C берега реки,
точками A и D острова, а линиями мосты.Такую фигуру называют графом, точки A, B, C, D называют вершинами графа, а отрезки кривых, соединяющие вершины, - дугами (ребрами) графа.
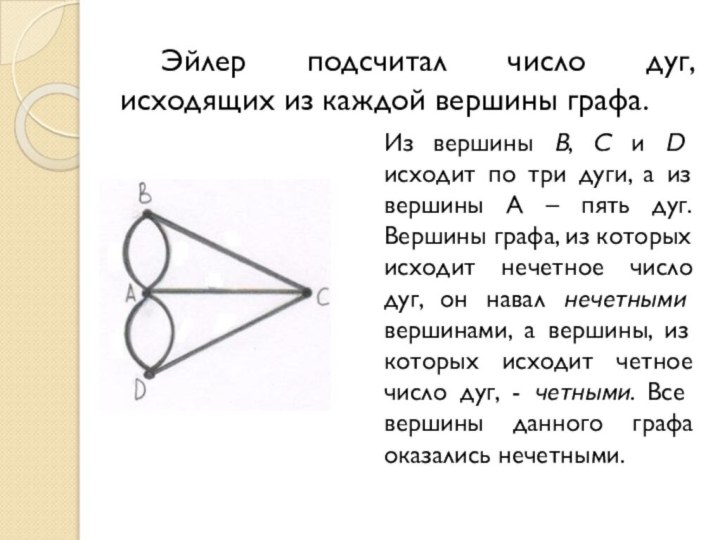
Слайд 6 Эйлер подсчитал число дуг, исходящих из каждой вершины
графа.
Из вершины B, C и D исходит по три
дуги, а из вершины A – пять дуг. Вершины графа, из которых исходит нечетное число дуг, он навал нечетными вершинами, а вершины, из которых исходит четное число дуг, - четными. Все вершины данного графа оказались нечетными.
Слайд 7
Свойства графа:
Число нечетных вершин графа всегда четно. Невозможно
начертить граф, который имел бы нечетное число нечетных вершин.
Если
все вершины графа четные, то можно одним росчерком начертить граф, при этом движение можно начать с любой вершины и закончить его в той же вершине.Граф только с двумя нечетными вершинами можно начертить одним росчерком, при этом движение нужно начать с одной из нечетных вершин и закончить в другой.
Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.
Леонард Эйлер
(1707-1783 гг.)
Слайд 8 Поскольку число нечетных вершин графа, соответствующего задаче о
семи мостах, оказалось равным четырем, то такой граф нельзя
изобразить одним росчерком, а следовательно, невозможно пройти по всем семи мостам, побывав на каждом из них по одному разу, и вернуться в начало пути.Достаточно было построить еще один мост через Преголю, например соединяющий участки B и D, и задача обхода одним маршрутом восьми мостов, каждого по одному разу, становится разрешимой.
Слайд 9
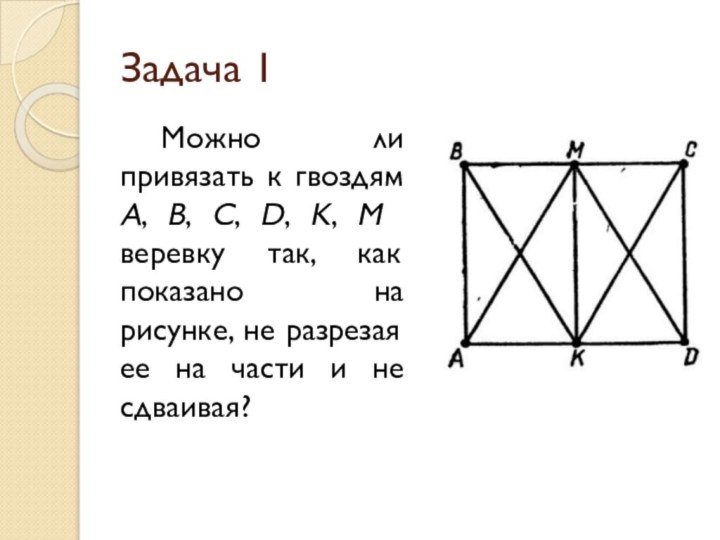
Задача 1
Можно ли привязать к гвоздям A, B,
C, D, K, M веревку так, как показано на
рисунке, не разрезая ее на части и не сдваивая?Слайд 10 Из рисунка видно, что из вершин A, B,
C и D исходят по три ребра, а из
вершин M и K – по пять. Получили, что все шесть вершин нечетны. Согласно свойству 4, найденному Эйлером, привязать веревку так, как требуется в условии задачи, невозможно.Слайд 11 Начертим теперь без отрыва карандаша от бумаги любую
самопересекающуюся кривую так, чтобы в одном случае росчерк закончить
в той же точке, с которой начали (рис. а), а в другом – в точке, отличной от начальной (рис. б). У нас получился граф, если точки самопересечения линии, а также ее начало и конец считать вершинами.Слайд 12 Подсчитаем теперь число дуг, исходящих из этих вершин.
Мы видим, что из любой вершины графа на рисунке
а исходит четное число дуг и из любой вершины графа на рисунке б, кроме вершин A и B, исходит также четное число дуг.Слайд 13 Фигура (граф), которую можно начертить одним росчерком (без
отрыва карандаша от бумаги и без повторения движения по
каждой из дуг), называется уникурсальной фигурой.
Слайд 14
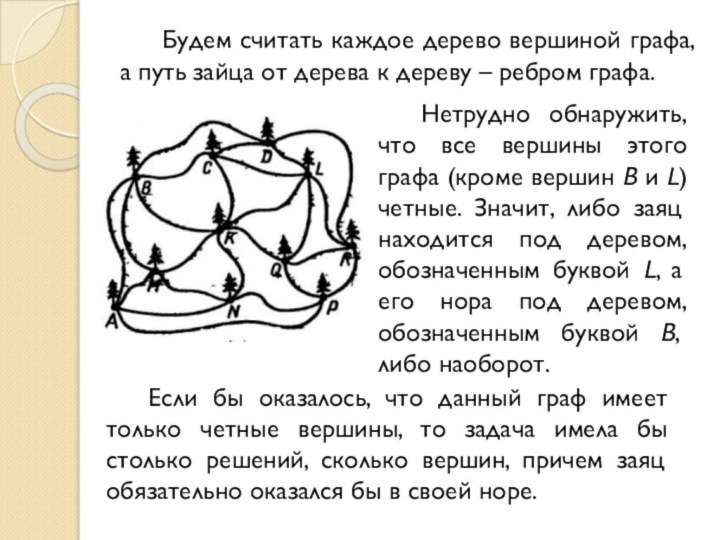
Задача 2
В небольшой роще находится заяц. Выскочив из
норы и бегая по снегу от дерева к дереву,
он оставил следы и, наконец, спрятался под одним из этих деревьев.Где сейчас находится заяц? Под каким деревом находится его нора? Сколько решений имеет задача?
Слайд 15 Будем считать каждое дерево вершиной графа, а путь
зайца от дерева к дереву – ребром графа.
Нетрудно обнаружить,
что все вершины этого графа (кроме вершин B и L) четные. Значит, либо заяц находится под деревом, обозначенным буквой L, а его нора под деревом, обозначенным буквой B, либо наоборот.Если бы оказалось, что данный граф имеет только четные вершины, то задача имела бы столько решений, сколько вершин, причем заяц обязательно оказался бы в своей норе.
Слайд 16
Задачи и упражнения
1. У какой уникурсальной фигуры начальная
и конечная точки совпадают? Начертите одну такую фигуру.
У фигуры,
у которой все вершины четные. Например, треугольник.Слайд 17 2. У какой уникурсальной фигуры начальная и конечная
точки не совпадают? Начертите одну такую фигуру.
У фигуры, у
которой только две нечетные вершины.Слайд 18 3. Какие из фигур, изображенных на рисунке, являются
уникурсальными? Изобразите стрелками один из вариантов обхода каждой из
уникурсальных фигур.Т.е. уникурсальными являются фигуры под буквами а, г и д.
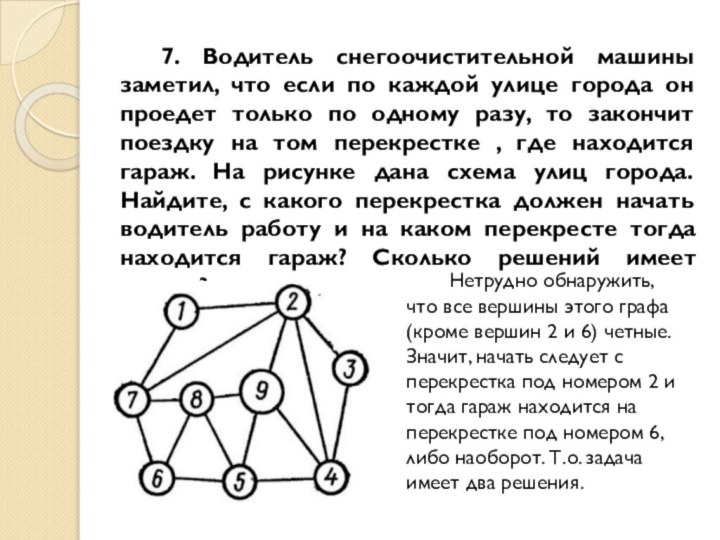
Слайд 20 5. Однажды пионеры попросили пионервожатую организовать экскурсию в
большой городской парк. Пионервожатая, показав ребятам план парка, предложила
им решить следующую задачу: «Найдите тот перекресток, откуда можно пройти по всем дорожкам только по одному разу». Решите и вы эту задачу.Нетрудно обнаружить, что все вершины этого графа (кроме вершин 6 и 7) четные. Значит, начать экскурсию следует с перекрестка под номером 6 и закончить на перекрестке под номером 7 либо наоборот.
Слайд 21 6. Каково наименьшее число росчерков, которыми можно начертить
каждую из данных на рисунке фигур?
Наименьшее число росчерков равно
половине числа нечетных вершин.а) 12:2=6
б)4:2=2
в) 5:2=2,5 (2 или 3; наименьшее 2)





























