- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему НАҚТЫ САННЫҢ n - ШІ ДӘРЕЖЕЛІ ТҮБІРІ ЖӘНЕ ОНЫҢ ҚАСИЕТТЕРІ
Содержание
- 2. Отан
- 3. 1. Функцияның анықталмаған интегралы дегеніміз не?
- 4. 2. Қисық сызықты трапеция дегенімізне?
- 5. 3. Қандай формуланы Ньютон – Лейбниц формуласы деп атайды?
- 6. 4. Анықталмаған интегралдың анықталған интегралдан айырмашылығы неде?
- 7. III. Жаңа сабаққа дайындық кезеңі:Дм.3. Жаңа сабақ
- 8. IV. Жаңа сабақДм.4 n-ші дәрежелі түбірдің
- 9. a санының n- ші дәрежелі түбірі
- 10. 2. Бөлшектен (қатынастан) түбір шығару үшін алымынан
- 11. 5 – мысал. 1)
- 12. 7 – мысал.
- 13. V. Жаңа сабақтан алған білімдерін тексеруДм.5 Венн
- 14. VI. Жаңа сабақты бекіту кезеңі:Дм.6 Есептер шығарту
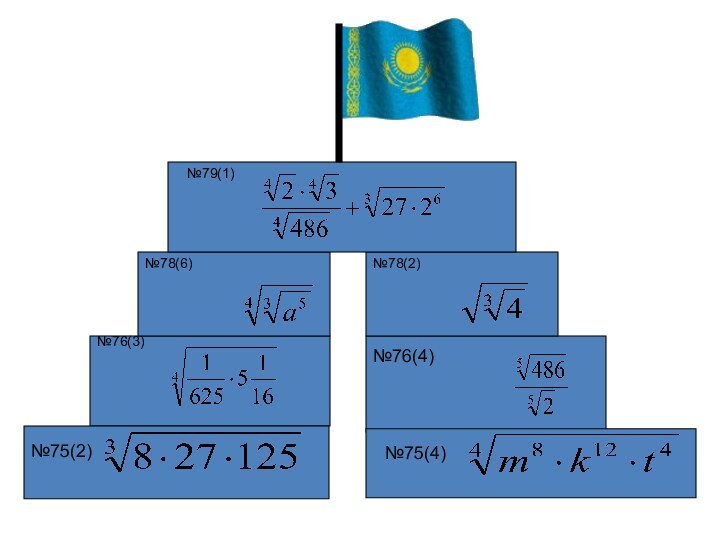
- 15. №76(3)№76(4)
- 16. Скачать презентацию
- 17. Похожие презентации
Отан















Слайд 7
III. Жаңа сабаққа дайындық кезеңі:
Дм.3. Жаңа сабақ жоспары:
Нақты
санның түбірі анықтамасымен танысасыңдар;
n-ші дәрежелі түбірдің қасиеттерімен танысамыз
және оларға мысалдар келтіреміз;n-ші дәрежелі түбірлерді салыстыруды мысалдар арқылы үйренеміз.
Слайд 8
IV. Жаңа сабақ
Дм.4 n-ші дәрежелі түбірдің анықтамасын
дәптерге жаздыру;
Дм5. анықтаманы және n-ші дәрежелі түбірдің қасиеттерін
түсіндіру;Анықтама. а санының n ші дәрежелі түбірі деп n ші дәрежесі а санына тең болатын b санын айтады.
Анықтама бойынша
мұндағы
Мұндағы n – түбірдің көрсеткіші және бірден өзгеше кез келген натурал сан, a – түбір таңбасының ішіндегі сан.
1 – мысал 8 санының үшінші дәрежелі түбірі 2-ге тең, себебі
2 – мысал. 3 және -3 сандары 81 санының төртінші дәрежелі түбірінің мәндері, өйткені
және демек
Слайд 9
a санының n- ші дәрежелі түбірі
болсын, онда анықтама бойынша
теңдеуін аламыз. Шыққан теңдеудің тақ болғанда бір ғана шешімі, жұп сан болғанда екі шешімі болатыны сәйкесінше 1-ші және 2- ші мысалдардан шығады.Дм.5 Енді n-ші дәрежелі түбірдің қасиеттерімен танысамыз:
1. Көбейтіндіден түбір шығару үшін әрбір көбейткіштен түбір шығарып, алынған нәтижелерді көбейту керек (көбейтіндіден түбір шығару ережесі):
3- мысал есептейік.
Шешуі. (1) формуланы қолданамыз:
Жауабы: -120
Дм.6 дәптермен жұмыс
(1) ережені оңнан солға қарай оқып, оған кері тұжырымдама беріңдер.
Слайд 10
2. Бөлшектен (қатынастан) түбір шығару үшін алымынан және
бөлімінен жеке түбір шығарып, бірінші нәтижені екінші нәтижеге бөлу
керек (бөлшектен түбір шығару ережесі):(2)
(2 ) ережені оңнан солға қарай оқып, оған кері тұжырымдама беріңдер.
4 – мысал. 1) 2) түбірлерінің мәндерін табайық.
Шешуі. (2) формуланы қолданамыз:
1) 2) Жауабы: 1) 2)
3. Түбірдің дәреже көрсеткіші мен түбір таңбасының ішіндегі өрнектің көрсеткішін қысқарту ережесі:
Слайд 11
5 – мысал. 1)
; 2)
түбірлерінің мәндерін ықшамдайық. Шешуі. (3) формуланы қолданамыз: 1) 2) Жауабы:1) ; 2)4. Түбірді дәрежеге шығару үшін түбір таңбасының ішіндегі өрнекті осы дәрежеге шығару керек (түбірді дәрежеге шығару ережесі);
(4)
6 – мысал 1) ; 2) түбірлерінің мәндерін анықтайық.
Шешуі. (4) формуланы қолданамыз:
1) 2)
Жауабы: 1)9; 2)
5. Түбірден түбір шығару үшін түбір таңбасының ішіндегі өрнекті өзгеріссіз қалдырып, көрсеткіші берілген екі түбірдің көрсеткіштерінің көбейтіндісіне тең түбірден шығару керек(түбірден түбір шығару ережесі)
(5)
Слайд 12 7 – мысал.
Түбірінің мәндерін есептейік.
Шешуі. (4) формуланы
қолданамыз:Жауабы: 2.
8- мысал 1) және сандарын салыстырайық.
демек
Жауабы:
2 ) және сандарын салыстырайық.
демек
Жауабы:
Слайд 13
V. Жаңа сабақтан алған білімдерін тексеру
Дм.5 Венн диаграммасы
бойынша жұмыс:
n – дәрежелі түбірдің n тақ болғанда
неше түбірі болады?n – дәрежелі түбірдің n жұп болғанда неше түбірі болады?





























