Слайд 2
Цели исследовательской работы:
Кем же был Я. Трахтенберг
и что его толкнуло к разработке
своей системы устного счета?
Какие
способы умножения содержит система устного счета у
Я. Трахтенберга?
Изучить методы и приемы быстрого счета и показать
возможность их использования для улучшения качества вычислений и для саморазвития.
Задачи:
Изучить приемы умножения многозначных чисел по системе
Я. Трахтенберга и проанализировать материал по данной теме.
Выбрать наиболее оптимальные методы и приемы быстрого
счета, познакомить с ними одноклассников и учащихся других классов.
Слайд 4
Математическая система Якова Трахтенберга описана в изданной в
США книге для детей «Мгновенная математика».
Ее автор — журналистка,
корреспондент Ассошиэйтед Пресс, Анна Кутлер
Слайд 5
Эта книга вышла в свет под названием «Быстрая
система элементарной математики Трахтенберга».
Тем временем в Цюрихе Яаков, чтобы доказать,
что систему может освоить каждый, начал заниматься с больным десятилетним ребенком.
Его «умственную отсталость» зафиксировали врачи.
В ходе этой работы выяснилось, что система имеет весьма неожиданные «побочные» свойства.
Слайд 6
Мальчик не только научился быстро производить сложнейшие вычисления,
но и значительно повысил свой коэффициент умственного развития.
Оказалось, что
процессы, которые происходят в мозге человека, когда он делает расчеты в уме
(это — один из неотъемлемых элементов системы Трахтенберга) заметно улучшают память и способность концентрироваться.
Сегодня многие медики пропагандируют систему Трахтенберга, рекомендуя пожилым пациентам тренировать ум и память, чтобы предотвратить нежелательные эффекты, которые возникают обычно в процессе старения.
Слайд 7
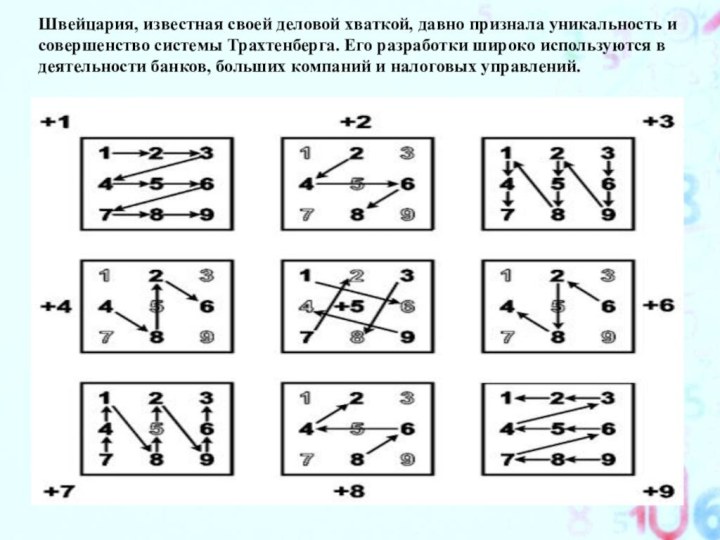
Швейцария, известная своей деловой хваткой, давно признала уникальность
и совершенство системы Трахтенберга. Его разработки широко используются в деятельности
банков, больших компаний и налоговых управлений.
Слайд 8
В огромном мире людей с давних пор известны
обладатели феноменальных способностей устного счета.
Ими владели многие ученые,
в частности Андре Ампер и Карл Гаусс.
А также и многие люди, чья профессия была далека от математики и науки в целом.
Ранее на эстраде были популярны выступления специалистов в устном счете.
Иногда они устраивали показательные соревнования между собой, проводившиеся в том числе и в стенах уважаемых учебных заведений, включая, например, Московский государственный университет имени М. В. Ломоносова.
Начиная с 2004 года, один раз в два года проводится Мировой чемпионат по вычислениям в уме, на который собираются лучшие из ныне живущих феноменальных счётчиков планеты
Слайд 9
Умножение на 11
Основные правила умножения на 11 заключаются
в следующем:
Последующая цифра множимого (число, которое умножается) записывается
как самая правая цифра результата.
Каждая следующая цифра множимого складывается со своим правым соседом и записывается в результат.
Первая цифра множимого становится самой левой цифрой результата.
Это последний шаг.
По системе Трахтенберга вы пишите результат, по одной цифре справа налево, точно так, как вы это делали ранее.
Слайд 10
Умножение на 12
Правило умножения на 12 заключается в
следующем:
Нужно удваивать поочередно каждую цифру и прибавлять к
ней ее «соседа».
В отличие от умножения на 11.
Теперь каждую цифру удваиваем, прежде чем прибавлять к ней «соседа»
Слайд 11
Умножение на 9
Правило умножения на 9: Вычитаем правую
цифру большого числа из десяти.
Это дает правую цифру
результата.
Возьмем поочередно каждую из следующих цифр самой последней, вычитаем ее из 9 и прибавляем соседа. В последнем шаге, когда будем рассматривать цифру 0, стоящую перед длинным числом, вычитаем из соседа, и полученное число будет самой левой цифрой результата
Слайд 12
Умножение на 7
Правило умножения на 7 очень похоже
на правило умножения на 6:
Мы смотрим только на
"цифру”:
если цифра четная, прибавляем к ней "половину” "соседа”, если цифра нечетная, то, кроме "половины” "соседа”, прибавляем еще 5.
Слайд 13
Умножение на 6
Правило умножения на 6: Прибавьте к
каждой цифре "половину” "соседа” и еще 5 в том
случае, если цифра четная и не имеет "соседа”; напишем ее снизу. Является ли "сосед” четным или нечетным - никакой роли не играет. Мы смотрим только на "цифру”: если она четная, прибавляем к ней "половину” "соседа”, если нечетная, то, кроме "половины” "соседа”, прибавляем еще 5.
Слайд 14
Умножение на 5
Вместо того чтобы прибавлять цифру, или
удваивать её мы используем цифру только для того, чтобы
определить её четность или нечетность. Если цифра нечетная, берём половину «соседа» и прибавляем 5; если цифра четная, пишем половину «соседа».
Слайд 15
Умножение на 4
Полностью правила таковы: Вычислите самую правую
цифру данного числа из 10 и прибавьте 5, если
цифра нечетная. Вычтите поочередно каждую цифру данного числа из 9, прибавьте 5, если цифра нечетная, и прибавьте половину соседа. Напишите под нулем перед заданным числом половину соседа этого нуля минус 1.
Слайд 16
Умножение на 3
Правило умножения на три выглядит следующим
образом: Первая цифра: вычтем ее из 10 и удвоим.
Если цифра не четная то прибавим. Средние цифры: вычтем из 9 и удвоим, затем прибавим половину соседа и 5, если цифра не четная. Самая левая цифра: разделим на 2 самую левую цифру большого числа и вычтем 2.
Слайд 17
Практическая значимость. В ходе работы мною было решено
множество примеров с различными алгоритмами умножениями многозначных чисел несколькими
альтернативными способами.
Это может заинтересовать одноклассников для расширения математического кругозора и послужит началом новых экспериментов.
Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны.
В старину пользовались более громоздкими и медленными приемами.
И если бы современный школьник мог отправиться на пятьсот лет назад, он поразил бы всех быстротой и безошибочностью своих вычислений.
Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.
Слайд 18
В книге В. Беллюстина «Как постепенно дошли люди
до настоящей арифметики» изложено 27 способов умножения, причем автор
замечает: «весьма возможно, что есть и еще способы, скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках».
И все эти приемы умножения соперничали друг с другом и усваивались с большим трудом. Рассмотрим наиболее интересные и простые способы умножения.
Слайд 19
Маленький замок
Способ очень похож на наш современный
«столбик».
Да еще и сразу определяются цифры старших разрядов.
Это бывает важно, если нужно быстро оценить величину.
Слайд 20
Решетчатый
Умножение чисел методом «ревность» или «решётчатое умножение»
Умножим, например,
числа 6827 и 345:
1. Вычерчиваем квадратную сетку и пишем
один из множителей над колонками, а второй - по высоте.
2. Умножаем число каждого ряда последовательно на числа каждой колонки. Последовательно умножаем 3 на 6, на 8, на 2 и на 7 .
4. Складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали.
Из результатов сложения цифр по диагоналям составляется число 2355315, которое и является произведением чисел 6827 и 345, то есть 6827 ∙ 345 = 2355315.
Вывод. Способ «решетчатое умножение» ничуть не хуже, чем общепринятый. Он даже проще, поскольку в клетки таблицы заносятся числа прямо из таблицы умножения без одновременного сложения, присутствующего в стандартном методе.
Слайд 21
Китайский способ
(графический)
Китайский способ
Предположим надо умножить 12
на 321.
На листе бумаги поочередно рисуем линии, количество
которых определяется из данного примера.
Рисуем первое число – 12.
Для этого сверху вниз, слева на право, рисуем:
одну зелёную палочку (1)
и две оранжевых (2).
Рисуем второе число – 321, снизу вверх, слева на право: три голубых палочки (3);
две красные (2); одну сиреневую (1).
Теперь простым карандашом отделяем точки пересечения и приступим к их подсчёту.
Двигаемся справа налево (по часовой стрелке): 2, 5, 8, 3.
Полученный результат прочитаем слева направо – 3852
Вывод.
Интересный способ, но проводить 9 прямых при умножении на 9 как-то долго и неинтересно, а потом еще точки пересечения считать.
Без сноровки сложно разобраться в делении числа на разряды.
В общем, без таблицы умножения не обойтись!
Слайд 22
Японский способ (круги)
Японский способ
Умножим 12 на 34.
Так как второй множитель двузначное число, а первая цифра
первого множителя 1, строим два одиночных круга в верхней строке и два двоичных круга в нижней строке, так как вторая цифра первого множителя равна 2.
Так как первая цифра второго множителя 3, а вторая 4, делим круги первого столбца на три части, второго столбца на четыре части.
Количество частей, на которые разделились круги и является ответом, то есть 12 х 34 = 408.
Вывод.
Способ очень похож на китайский графический.
Только прямые заменены кругами.
Легче определять разряды у числа, однако рисовать круги – менее удобно.
Слайд 23
Таблица Василия Оконешникова
Требуется умножить 15647 х 5.
Сразу вспоминаем большую «кнопку» 5 (она посередине) и на
ней мысленно находим маленькие кнопочки 1, 5, 6, 4, 7 (они также расположены, как на калькуляторе).
Им соответствуют числа 05, 25, 30, 20, 35. Полученные числа складываем: первая цифра 0 (остаётся без изменения), 5 мысленно складываем с 2, получаем 7 – это вторая цифра результата, 5 складываем с 3, получаем третью цифру - 8, 0+2=2, 0+3=3 и остаётся последняя цифра произведения – 5. В результате получилось 78 235.
Вывод.
Способ очень удобный, но нужно выучить наизусть или всегда иметь под рукой таблицу.
Слайд 24
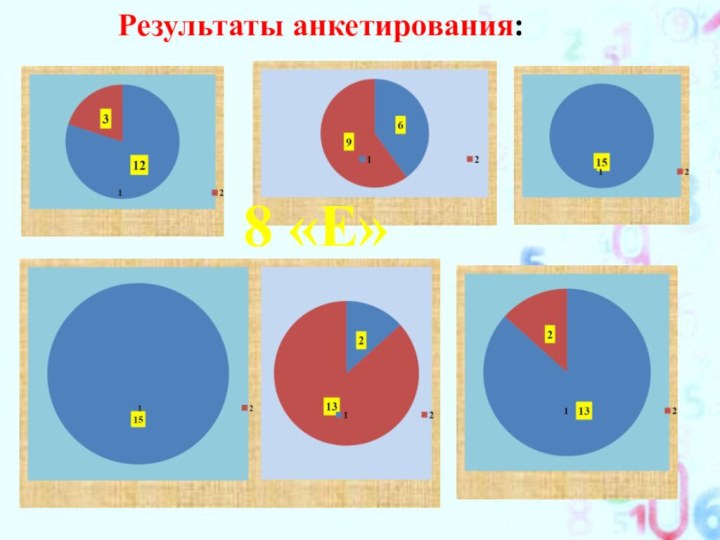
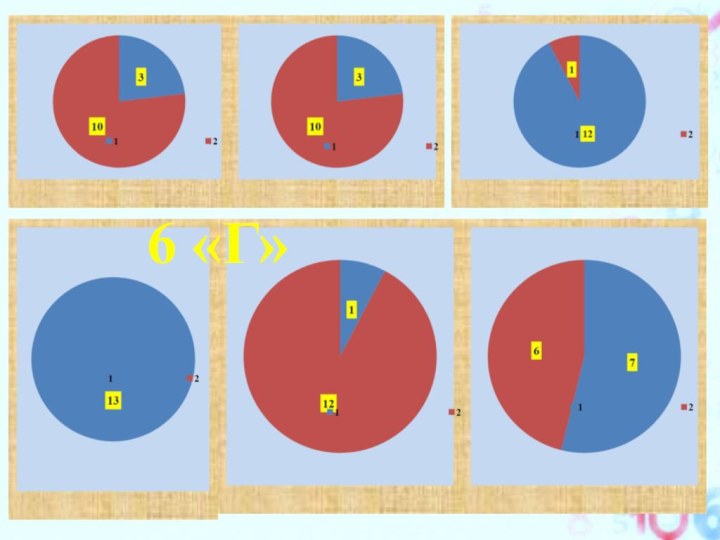
Только факты
Я провела анкетирование учащихся 6-ых и 8-ых
классов по следующим вопросам:
Умеешь ли ты быстро и
правильно считать?
Как часто ты пользуешься калькулятором?
Знаешь ли ты какие-либо приемы быстрого счета?
Как ты думаешь, развивает ли умение считать такие
функции, как память, внимание, способность сосредоточиться?
5. Знаете ли вы способы умножения системы устного счета у Я. Трахтенберга?
6. Будете ли вы использовать "приёмы быстрого счёта" на уроках математики?