Слайд 2
«Великая цель образования – это
не знания, а действия. … Дороги не те знания,
которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы»
Герберт Спенсер
Слайд 3
Целями проблемного обучения являются:
усвоение результатов научного познания,
а также овладение способами познания;
формирование и развитие интеллектуальной,
мотивационной
сфер школьника;
- развитие индивидуальных способностей учащихся.
Слайд 4
Три вида проблемного обучения:
проблемное изложение знаний.
привлечение
учащихся к поиску
на отдельных этапах изложения знаний.
исследовательский метод.
Слайд 5
Учебный процесс в условиях проблемного
обучения имеет следующую
структуру:
Слайд 6
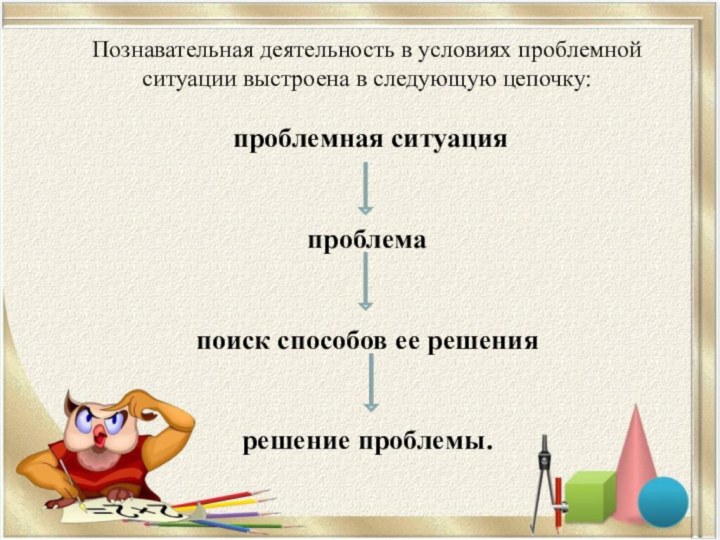
Познавательная деятельность в условиях проблемной
ситуации выстроена в
следующую цепочку:
проблемная ситуация
проблема
поиск способов ее решения
решение проблемы.
Слайд 7
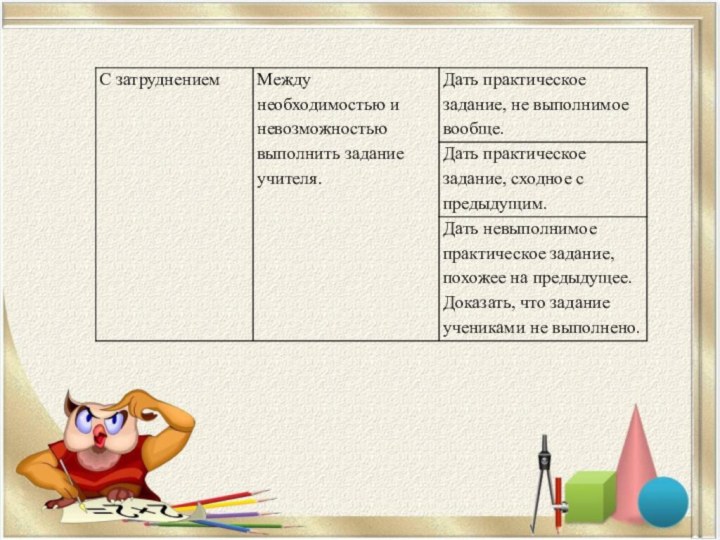
Проблемные ситуации бывают двух типов:
возникшие с удивлением
и
возникшие с затруднением.
Слайд 11
Подвести обучающихся к противоречию и предложить
им самим
найти способ его разрешения.
5 класс. Тема: «Сложение и вычитание
смешанных чисел»
- Вычислить:
Возможные варианты ответа:
Слайд 12
Создание проблемных ситуаций через умышленно допущенные учителем ошибки.
7
класс.
Тема «Линейные уравнения с одной переменной».
Решаю быстро
уравнение:
(3х + 7) ∙ 2 – 3 = 17
6х + 14 – 3 = 17
6х = 17 – 14 – 3
6х = 0
х = 0
Естественно при проверке ответ не сходится. Проблемная ситуация. Ищут ошибку, решают проблему.
Лучше предложить найти ошибку в уже записанном решении.
Результат - внимательность и заинтересованность на уроке.
Слайд 13
2.Создание проблемных ситуаций через использование занимательных заданий.
7 класс.
Тема: «Линейная функция»
Приглашаю к доске ученика, даю ему карточку,
на которой
написано у = х + 5. На доске заготовлена таблица:
Ученик из класса называет какое-нибудь значение х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение у. Затем другой ученик из класса называет другое значение х и ученик у доски проделывает те же операции. Задача класса – “угадать” формулу, записанную на карточке. Проблемная ситуация создана. Выигрывает тот ученик, который первый назовет формулу.
Результат – активизация мыслительной деятельности.
Слайд 14
3. Создание проблемных ситуаций через решение задач, связанных
с жизнью.
5 класс. Тема «Проценты»
До проведения акции стиральная машина
стоила 11750 рублей. Продавец снизил ее стоимость на 15%. Какую сумму нам надо будет заплатить при покупке этой стиральной машины?
Вопрос: «А как же мы вам поможем, если мы не знаем, что такое процент?»
Проблемная ситуация создана. В конце урока решают задачу до конца.
Слайд 15
6. Создание проблемных ситуаций через выполнение небольших исследовательских
заданий.
9 класс. Тема «Длина окружности»
Ещё древние греки находили длину
окружности по формуле С= π ∙ d, где d - это диаметр окружности.
Вопрос: а что же такое π?
Работаем в парах, выполняя необходимые измерения.
1. Построить окружность заданного радиуса и ниткой измерить длину своей окружности, распрямить нитку, длина нитки примерно равна длине окружности . Чтобы получить более точный результат, нужно это проделать несколько раз.
Слайд 16
Занесите данные в следующую таблицу.
2.Вычислите диаметр окружности. Данные
занесите в таблицу.
3.Найдите значение π, как неизвестного множителя.
4.Каждой
паре занести вычисленное значение π в таблицу на доске.
Исследование проведено. На уроке кроме исследовательской работы удачно использовалась работа в парах. Проблема решена.
Слайд 17
4. Создание проблемных ситуаций через выполнение практических заданий.
7
класс. Тема: «Неравенство треугольника».
Теорему о неравенстве треугольника вводим
при изучении темы «Построение треугольника по трем элементам», решая задачу на построение треугольника по трем его сторонам. Предлагаем ученикам построить с помощью циркуля и линейки треугольник со сторонами: а) 5см; 6см; 7см; б) 1см; 2см; 3см.
Ребята работают самостоятельно и приходят к тому, что построить треугольник в последнем примере не удается. Возникает проблема: «При каких же условиях существует треугольник»? Чертежи, полученные учащимися при решении этой задачи дают возможность легко сделать вывод: «Каждая сторона треугольника меньше суммы двух других сторон». Доказываем полученную теорему.
Слайд 18
5. Создание проблемных ситуаций через противоречие нового материала
старому, уже известному.
7 класс. Тема «Формулы сокращенного умножения»
Вычисляем (2
∙ 5)²= 2² ∙5² = 100
(3 ∙ 4)²= 3² ∙ 4² = 9 ∙ 16 = 144
(5 : 6)² = 5² : 6² = 25 : 36
(3 + 4)² = 3² + 4² = 9 + 16 = 25
Попробуйте сосчитать иначе - ( 3 + 4)² =7² = 49
Проблемная ситуация создана. Почему разные результаты?
( 3 +4)² ≠ 3² + 4²
В результате возникает необходимость ввести формулу кварата суммы и разности двух выражений.
Слайд 19
7. Создание проблемных ситуаций через решение задач с
недостающими данными.
7 класс. Тема: Внешний угол треугольника.
Внешний угол равнобедренного
треугольника равен 75°. Найдите углы этого треугольника.
Возникает проблема, где именно располагается внешний угол. При дальнейшем анализе условия появляются и два способа решения этой задачи.
Слайд 20
Побуждение делать сравнения, обобщения,
выводы из ситуации, сопоставлять
факты.
5 класс. Тема: «Упрощение выражений»
Ранее мы изучили свойства
сложения и умножения, я предлагаю,
используя эти свойства решить устно заданные примеры, назвать свойство,
которое применяется в каждом примере:
А) 27+174+73;
Б) 50∙19∙2;
В) 64+(79+36);
Г) 135∙12+8∙135.
Слайд 21
«Обманные задачи»:
1. Постройте прямоугольник со сторонами 2, 3
и 5 см.
2. Больший угол треугольника равен 50°.
Найдите остальные углы.
3. Две стороны треугольника перпендикулярны третьей. Определите вид треугольника.
4. Внешний угол при основании равнобедренного треугольника равен 75°. Найдите углы треугольника.
5. Диагональ ромба в два раза больше его стороны. Найдите углы ромба.
Слайд 22
Создание проблемных ситуаций через решение задач , связанных
с жизнью
5 кл. Тема «Периметр прямоугольника»
Семья Димы летом переехала
в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный м. изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей.
Проблемная ситуация: нужно найти длину изгороди (периметр прямоугольника).
Слайд 23
Создание проблемных ситуаций на уроках математики не только
формирует ту систему математических знаний, умений и навыков, которая
предусмотрена программой, но и самым естественным образом развивает у школьников творческую активность.
Нельзя заставлять ребёнка слепо штудировать предмет в погоне за общей успеваемостью. Необходимо давать ему возможность экспериментировать и не бояться ошибок, воспитывать у учащихся смелость быть не согласным с учителем.
ЗАКЛЮЧЕНИЕ