Слайд 2
Механические характеристики АДФ и АДК:
Асинхронные электродвигатели нашли широкое
применение в промышленности благодаря простоте конструкции, надежности и экономичности
в эксплуатации, минимальной стоимости и возможности питания от электрической сети переменного тока.
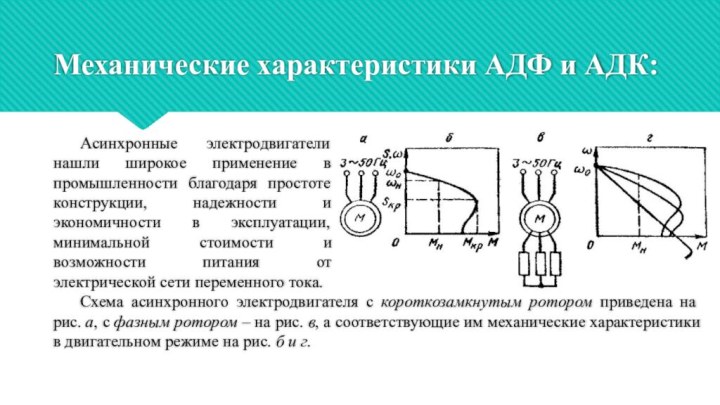
Схема асинхронного электродвигателя с короткозамкнутым ротором приведена на рис. а, с фазным ротором – на рис. в, а соответствующие им механические характеристики в двигательном режиме на рис. б и г.
Слайд 3
Особенности электромеханических процессов в АД:
Несмотря на простоту физических
явлений полное математическое описание процессов в асинхронной машине весьма
сложно. Эта сложность порождена несколькими причинами:
– все напряжения, токи, потокосцепления – переменные, т.е. характеризуются частотой, амплитудой, фазой или соответствующими векторными величинами;
– взаимодействуют движущиеся контуры, взаимное положение которых изменяется в пространстве;
– магнитный поток нелинейно связан с намагничивающим током (проявляется насыщение магнитной цепи), активные сопротивления роторных цепей зависят от частоты (проявляется эффект вытеснения тока), сопротивления всех цепей существенно зависят от температуры и т.п.
Слайд 4
Допущения при расчете механических характеристик АД:
Для расчета статической
механической характеристики принимают следующие допущения:
– ЭДС, токи, потокосцепления –
синусоидальны во времени и пространстве;
– проводимость намагничивающего контура постоянна (не учитывается кривая намагничивания);
– параметры цепей постоянны (активные сопротивления и индуктивности не зависят от частоты, насыщение не влияет на индуктивные сопротивления рассеяния х1 и х2);
– не учитываем моменты, создаваемые высшими гармониками потока и тока, расчет ведем по первой гармонике;
– гистерезис и вихревые токи отсутствуют;
– механические потери на трение и вентиляцию отсутствуют (отнесены к статическому моменту).
Слайд 5
П-образная схема замещения АД:
Слайд 6
Математическое описание характеристик АД:
Для получения математического описания характеристик
АД применяется его схема замещения, в которой цепи статора
и ротора объединены электрически, хотя в действительности эти цепи связаны только электромагнитно. Получить такую схему замещения позволяет приведение параметров цепи ротора к цепи статора. Приведение (перерасчет) осуществляется с помощью коэффициента трансформации двигателя по ЭДС:
где Е1 и Е2к – фазные ЭДС статора и ротора при неподвижном роторе; Uфн – фазное напряжение сети.
Слайд 7
Математическое описание характеристик АД:
Формулы приведения:
где приведенные значения имеют
индекс «пр».
Зависимость приведенного тока ротора от скольжения I2пр(s) описывается
выражением, полученным на основании схемы замещения:
где Хк=Х1+Х2пр – индуктивное сопротивление КЗ из схемы замещения АД
Слайд 8
Электромеханическая характеристика АД:
На рис. представлены электромеханические характеристики АД
как зависимости ω=f(I1), ω = f(I'2), S = f(I'2,I1).
Проведем
анализ характеристик.
1. При S = 0; ω= ω0; I'2 = 0; I1 = I0 – точка идеального холостого хода.
2. При S = 1; ω = 0; I1 = Iкз = Iпуск – точка короткого замыкания.
3. При S = –R'2/R1; ω = ω 0(1 – S1); I'2 = Imax = Uф/Xк – точка максимального тока ротора, лежащая в области отрицательных скольжений.
Слайд 9
Электромеханическая характеристика АД:
4. При
Слайд 10
Механическая характеристика АД:
Для построения механической характеристики АД рассмотрим
баланс мощности в цепи ротора.
Потери мощности в цепи ротора
где Pэм – электромагнитная мощность; Р2 – полезная механическая мощность на валу.
Так как потери в роторе ΔP2 зависят от S, их называют потерями скольжения. С другой стороны, ΔP2 = 3I22'R2', тогда M = (3I22'R2')/(ω0S), подставив I2', получим уравнение механической характеристики АД:
Слайд 11
Механическая характеристика АД:
Если в выражении уточненной формулы Клосса
принять R1 = 0 (для двигателей большой и средней
мощности R1 = 0,1…0,15·XK), тогда a = R1 / R′2 = 0, то мы получим упрощенную формулу Клосса
Также критическое скольжение можно определить по формуле:
где Sн – номинальное скольжение; λк – отношение критического момента к номинальному.
Слайд 12
Механическая характеристика АД:
На рис. представлена механическая характеристика АД
в различных режимах работы.
Проведем анализ механической характеристики АД .
При
S = 0, ω = ω0, M = 0 – точка идеального холостого хода АД.
При S = 1, ω= 0, M = Mкз = Mпуск – точка короткого замыкания АД.
При S = Sк(двиг), M = Mк(двиг), S = –Sк(ген), M = Mк(ген), – точки экстремума (максимума М).
Слайд 13
Задача:
Рассчитать естественную механическую характеристику АДК типа А2-72-4 с
Рн=30 кВт; Uн=380 В; nн=1460 об/мин; λк =2.
Решение:
1. Номинальный
момент двигателя Мн = Рн /ωн = Рн /(π nн /30);
2. Критический момент АД Мк = λк Мн ;
3. Номинальное скольжение sн = (n0 – nн) / n0 ;
4. Критическое скольжение
5. Уравнение механической характеристики М = 2Мк/(s/sк + sк/s)
Слайд 14
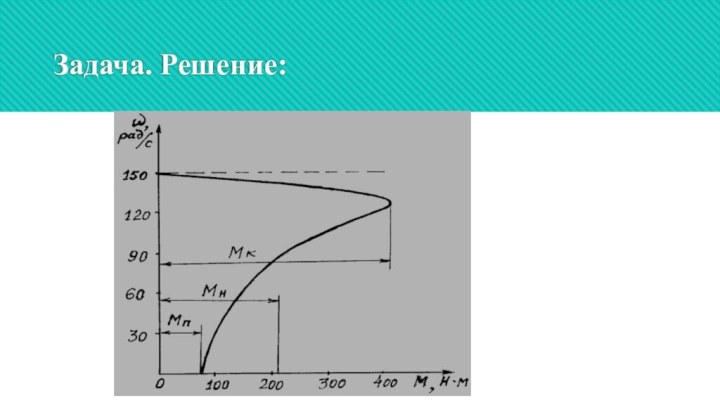
Задача. Решение:
1. Мн = Рн /ωн = Рн
/(π nн /30) = 30000 / (π 1460/30) =
205 Нм;
2. Мк = λк Мн = 2 205 = 410 Нм;
3. sн = (n0 – nн) / n0 = (1500 – 1460)/1500 = 0,0266;
4.
5. Уравнение механической характеристики М = 820/(s/0,1 + 0,1/s);