Презентация на тему Работа с одаренными. Геометрические задачи.

Доказать, что никакая фигура не может иметь ровно
два центра

симметрии.
Решение. Доказательство основывается на том факте, что точка,
симметричная одному центру симметрии относительно другого,
также является центром симметрии.
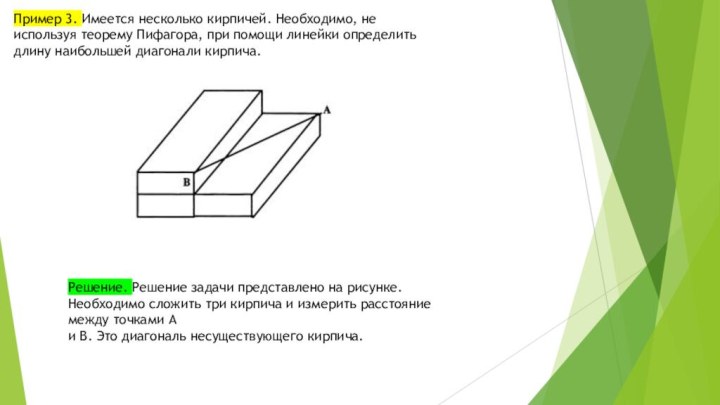
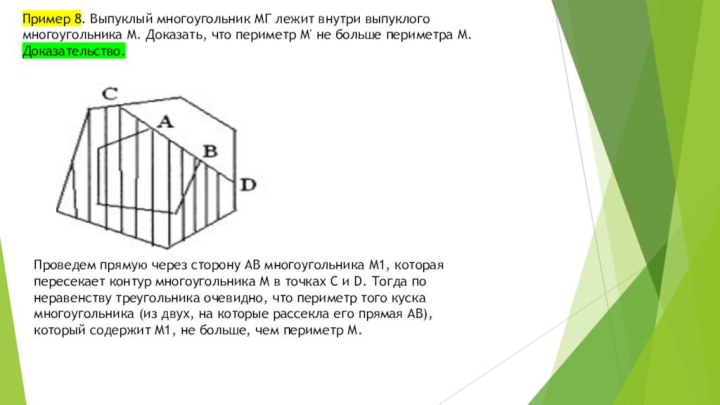
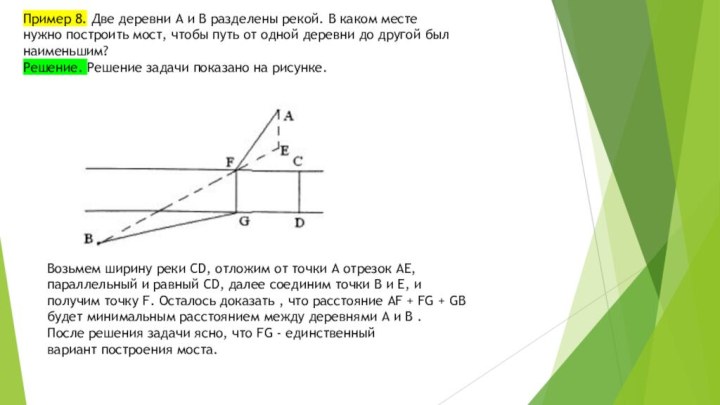
Пример 2. Разрезать произвольный треугольник на три части, из
которых можно составить прямоугольник.
Решение. Для решения задачи необходимо разрезать треугольник
по средней линии, а отрезанный треугольник еще и по высоте.
Сложение получившихся частей в прямоугольник не составляет труда.
Следующая задача встречается у И. Ф. Шарыгина.

теорему Пифагора, при помощи линейки определить
длину наибольшей диагонали кирпича.
Решение.

Решение задачи представлено на рисунке.
Необходимо сложить три кирпича и измерить расстояние между точками А
и В. Это диагональ несуществующего кирпича.

и С на плоскости АС > |АВ - ВС|.
Примечание.

Сформулировав теорему, дадим ее очевидное
геометрическое истолкование: длина любой стороны треугольника
не меньше модуля разности длин двух других сторон.

Теорема 2. Длина любой стороны треугольника не превосходит
его полупериметра.
Примечание. Один из самых распространенных способов
доказательства геометрических неравенств состоит в том, что
применяется неравенство треугольника, возможно, с использованием
некоторых дополнительных соображений.

Пример 4. Длина стороны АС треугольника ABC равна 3,7,
длина стороны АВ — 0,5. Известно, что длина ВС — целое число.
Какова эта длина?
Решение. По теореме 1 3,7 > |0,5 — ВС|, однако ВС — число
натуральное, поэтому 3,7 > ВС — 0,5, откуда ВС < 4,2. Далее ясно,
что ВС = 4. Подумайте, почему ВС не может равняться трем.

леса в заданной точке. Ему
необходимо дойти до шоссе, которое

представляет собой прямую
линию, где у него собранные грибы заберет сын, приехавший на
машине; а далее зайти в лес в другой точке, в которой ожидает его
жена. Как ему это сделать, пройдя по самому короткому пути?

Решение.

Пусть грибник выходит из леса в точке А, а должен зайти в лес в
точке В. Для решения задачи симметрично прямой — шоссе отобразим
точку В, получив точку В1. Далее, проведя прямую АВ1, получим точку
D, которая и является искомой в задаче точкой. BD = B'D, ВС = В'С,
тогда ясно, что для любой другой точки F AF + FB' > AD + DB'.
Расстояние AD + BD является наименьшим для выхода на шоссе из
леса и захода в лес в заданной точке (D).

муха М и два паука П, и П2. Пауки,

которые могут
перемещаться только по внутренним поверхностям граней,
одновременно начинают бежать к мухе. Какой из пауков быстрее ее достигнет,
если расстояния СП, = - я, MB' = - а\ Dn2 = - я, где а - длина
ребра куба.

Решение. Нарисуем необходимую нам для решения часть развертки куба:

до мухи М быстрее, чем паук П2.

ABC. Доказать,
что АО + ОС < АВ + ВС.
Продолжим

отрезок АО до пересечения со стороной треугольника D.
Далее сложим неравенства треугольника
АВ + BD > АО + OD и

М. Доказать, что периметр М' не больше периметра М.
Доказательство.
Проведем

прямую через сторону АВ многоугольника М1, которая
пересекает контур многоугольника М в точках С и D. Тогда по
неравенству треугольника очевидно, что периметр того куска
многоугольника (из двух, на которые рассекла его прямая АВ),
который содержит М1, не больше, чем периметр М.

рекой. В каком месте
нужно построить мост, чтобы путь от

одной деревни до другой был
наименьшим?
Решение. Решение задачи показано на рисунке.

Возьмем ширину реки CD, отложим от точки А отрезок АЕ,
параллельный и равный CD, далее соединим точки В и Е, и
получим точку F. Осталось доказать , что расстояние AF + FG + GB
будет минимальным расстоянием между деревнями А и В .
После решения задачи ясно, что FG - единственный
вариант построения моста.

км, от Кисловодска до
Минеральных Вод 55 км, от Минеральных

Вод до Невинномысска 125 км, а от Невинномысска до Ставрополя 50 км.
Каково расстояние от Ставрополя до города Минеральные
Воды?
2. Докажите, что в выпуклом четырехугольнике сумма
диагоналей больше его полупериметра и меньше периметра.
3. Докажите, что в выпуклом пятиугольнике сумма длин
диагоналей больше периметра и меньше удвоенного периметра.
4. Внутри треугольника взяли две произвольные точки.
Доказать, что расстояние между ними не превосходит
полупериметра треугольника.
5. Точку А, лежащую внутри острого угла, отразили
симметрично относительно сторон угла. Полученные точки В и С
соединили и точки пересечения отрезка ВС со сторонами
угла DE (см. рис.) Доказать, что.

Минеральных Вод, от
Минеральных Вод до Невинномысска и от Невинномысска
до

Ставрополя равна расстоянию от Ставрополя до
Кисловодска. Делаем вывод, что все города находятся на одной
трассе (прямой).
2. Пусть диагонали пересекаются в точке О. Требуемые
неравенства легко выводятся из неравенств треугольника для
треугольников ОАВ, ОВС, OCD, ODA и для треугольников
ABC, BCD, CDA и DAB.
3. Решение аналогично решению примера 10.
4. Продолжите отрезок, соединяющий эти точки в обе стороны
до пересечения с контуром треугольника.
5. Воспользуйтесь тем, что AD = BD, АЕ = ЕС, и неравенством
AD + АЕ > DE.

ограничились
только неравенством треугольника и сознательно не
рассматривали расчетные

задачи. Ведь мы только начинаем
подготовку к решению олимпиадных задач. По
большому счету, эта презентация предназначена для учеников
5—7 классов, хотя она может оказаться полезной и для
школьников возрастом постарше.