Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Аналитическая геометрия

Содержание

СодержаниеГеометрические векторыЛинейные операции над векторами и их свойстваСкалярное произведение векторовРасстояние между точками
Аналитическая геометрияЛекции по математике для студентов I курса СодержаниеГеометрические векторыЛинейные операции над векторами и их свойстваСкалярное произведение векторовРасстояние между точками Геометрические векторыГеометрический вектор – это направленный отрезок.Обозначения: , Длина вектора – это расстояние между начальной и конечной точками.Обозначения: Геометрические векторыВекторы называют коллинеарными, если они лежат на одной прямой или на Геометрические векторыВекторы называют компланарными, если они лежат в одной плоскости.Два вектора называют Линейные операции над векторамиЛинейными операциями над векторами являются сложение векторов и умножение 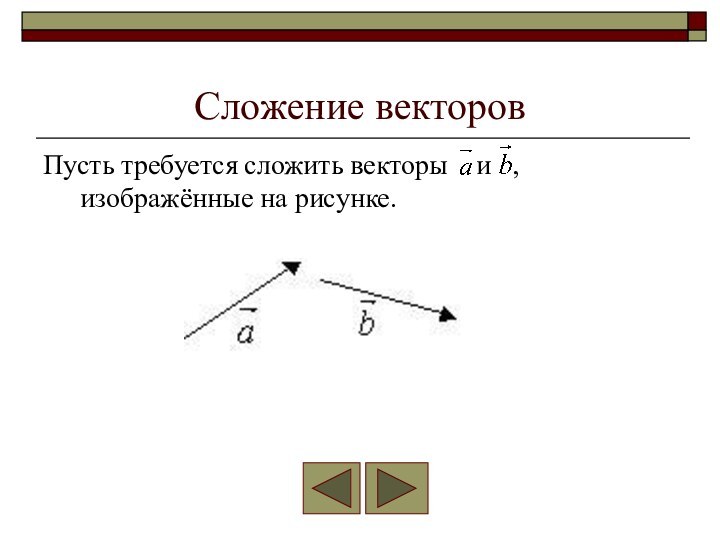Сложение векторовПусть требуется сложить векторы и , изображённые на рисунке. Правило треугольникаПараллельным переносом совместим конец вектора с началом вектора . Тогда Правило параллелограммаПараллельным переносом совместим начало вектора и начало вектора . Достроим Свойства сложения векторовКоммутативность:Ассоциативность:Существование нулевого вектора такого, что Для любого вектора существует Разность векторовМожно доказать, что для любых векторов и Произведение вектора на числоПроизведением вектора на вещественное Свойства произведенияАссоциативность сомножителей: _Дистрибутивность Скалярное произведение векторовУгол между векторами будем обозначать Углом между двумя векторами будем Скалярное произведение векторовСкалярным произведением двух геометрических векторов называется число, равное произведению длин Скалярное произведение векторовЕсли , то Пример 1.Вычислить скалярное произведение векторов и , если Скалярное произведение векторовНеобходимое и достаточное условие перепендикулярности векторовСкалярное произведение двух ненулевых векторов Свойства скалярного произведенияКоммутативность: Ассоциативность: Дистрибутивность относительно суммы векторов:Скалярное произведение двух ненулевых векторов Угол между векторамиТак как Рене Декарт предложил координатный методМетод позволяет описывать геометрические объекты аналитически, т.е. на языке алгебры. 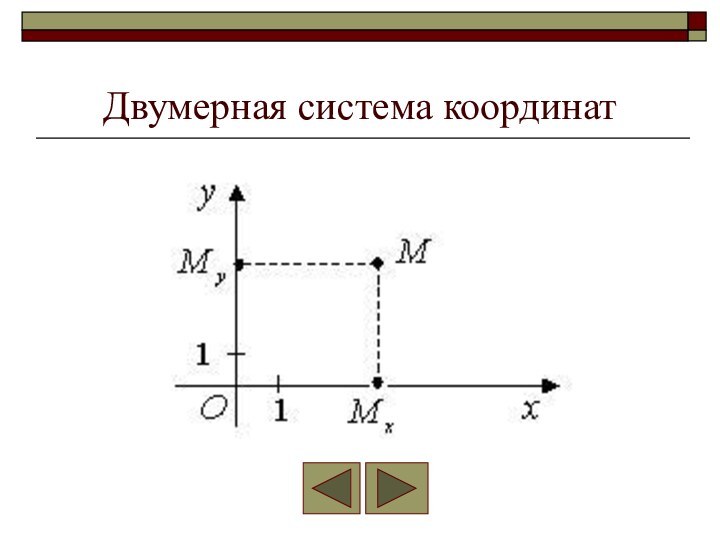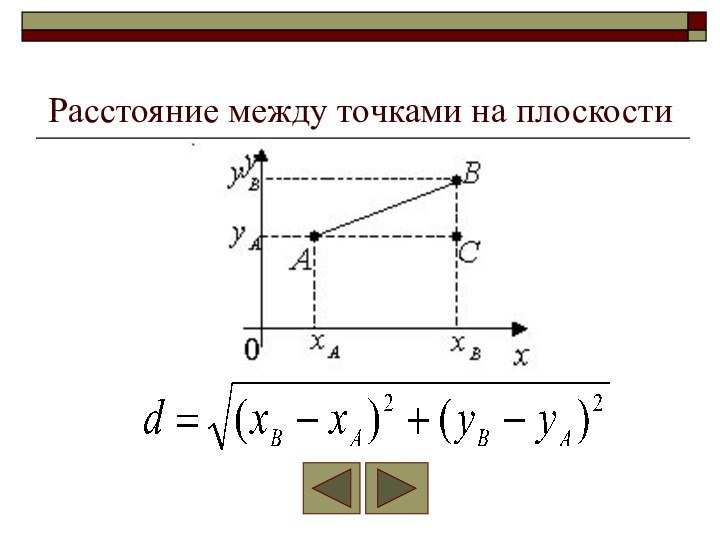Одномерная система координатПрямая с заданным направлениемЗадана точка – начало координатВыбран единичный масштаб Координата точкиКоордината точки равна расстоянию от начала координат до заданной точкиКоордината положительна, Двумерная система координат Трёхмерная система координат Правая система координатЛевая система координат Расстояние между точками на прямой линии Расстояние между точками на плоскости Расстояние между точками в геометрическом пространстве Расстояние между точками пространстваДлина вектора – это расстояние между двумя точками: началом Расстояние между точками пространстваИз определения скалярного произведения следует, что Свойства длины вектора 1. 2. Пример 3.Вычислить длину вектора , если Ортонормированный базис Пример 4.Известны координаты начальной и конечной точек вектора : A(1, 3, Пример 2.Известны координаты начальной и конечной точек вектора : A(1, 3, Пример 2.Известны координаты начальной и конечной точек вектора
Слайды презентации

Слайд 2 Содержание
Геометрические векторы
Линейные операции над векторами и их свойства
Скалярное

СодержаниеГеометрические векторыЛинейные операции над векторами и их свойстваСкалярное произведение векторовРасстояние между точками

произведение векторов
Расстояние между точками

Слайд 3 Геометрические векторы
Геометрический вектор – это направленный отрезок.
Обозначения:

Геометрические векторыГеометрический вектор – это направленный отрезок.Обозначения: ,

Слайд 4 Длина вектора – это расстояние между начальной и

Длина вектора – это расстояние между начальной и конечной точками.Обозначения:

конечной точками.
Обозначения: , или просто

АВ, а.
Вектор называют нулевым, если его начало и конец совпадают.
Обозначение: .

Геометрические векторы

Слайд 5 Геометрические векторы
Векторы называют коллинеарными, если они лежат на

Геометрические векторыВекторы называют коллинеарными, если они лежат на одной прямой или

одной прямой или на параллельных прямых.
Обозначение:

.

Слайд 6 Геометрические векторы
Векторы называют компланарными, если они лежат в

Геометрические векторыВекторы называют компланарными, если они лежат в одной плоскости.Два вектора

одной плоскости.
Два вектора называют равными, если они коллинеарные, имеют

одинаковую длину и направление.
Свободным называют вектор, который можно перемещать в пространстве параллельно его направлению.

Слайд 7 Линейные операции над векторами
Линейными операциями над векторами являются

Линейные операции над векторамиЛинейными операциями над векторами являются сложение векторов и

сложение векторов и умножение вектора на число.
Суммой двух геометрических

векторов и называется вектор, который можно построить или по правилу треугольника или по правилу параллелограмма.

Слайд 8 Сложение векторов
Пусть требуется сложить векторы и

Сложение векторовПусть требуется сложить векторы и , изображённые на рисунке.

, изображённые на рисунке.

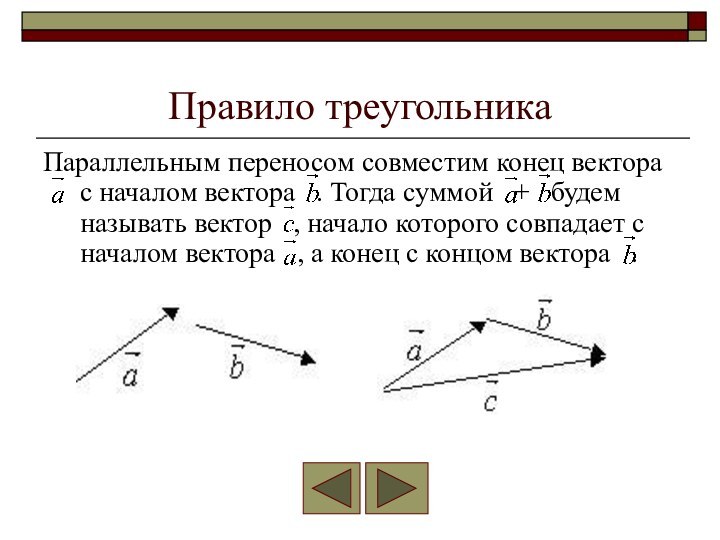
Слайд 9 Правило треугольника
Параллельным переносом совместим конец вектора с началом

Правило треугольникаПараллельным переносом совместим конец вектора с началом вектора . Тогда

вектора . Тогда суммой + будем

называть вектор , начало которого совпадает с началом вектора , а конец с концом вектора .

Слайд 10 Правило параллелограмма
Параллельным переносом совместим начало вектора и начало

Правило параллелограммаПараллельным переносом совместим начало вектора и начало вектора . Достроим

вектора . Достроим параллелограмм на концах векторов. Суммой

векторов и будем называть вектор , являющийся диагональю параллелограмма, начало которого совпадает с началом векторов и .

Слайд 11 Свойства сложения векторов
Коммутативность:
Ассоциативность:
Существование нулевого вектора такого, что
Для

Свойства сложения векторовКоммутативность:Ассоциативность:Существование нулевого вектора такого, что Для любого вектора существует

любого вектора существует противоположный вектор ( )такой,

что

Слайд 12 Разность векторов
Можно доказать, что для любых векторов

Разность векторовМожно доказать, что для любых векторов и существует

и существует такой вектор ,

который, будучи сложен с , даст вектор :
Такой вектор называют геометрической разностью:

Слайд 13 Произведение вектора на число
Произведением вектора

Произведение вектора на числоПроизведением вектора на вещественное число

на вещественное число называется вектор

, имеющий длину, равную произведению чисел и направление, совпадающее с направлением вектора , если , и противоположное, если .

Слайд 14 Свойства произведения
Ассоциативность сомножителей:

Свойства произведенияАссоциативность сомножителей: _Дистрибутивность относительно суммы векторов:Дистрибутивность относительно суммы чисел:Существование числа 1:

_
Дистрибутивность относительно суммы векторов:
Дистрибутивность относительно суммы

чисел:
Существование числа 1:

Слайд 15 Скалярное произведение векторов
Угол между векторами будем обозначать
Углом

Скалярное произведение векторовУгол между векторами будем обозначать Углом между двумя векторами

между двумя векторами будем называть угол, который не превосходит

.

Слайд 16 Скалярное произведение векторов
Скалярным произведением двух геометрических векторов называется

Скалярное произведение векторовСкалярным произведением двух геометрических векторов называется число, равное произведению

число, равное произведению длин этих векторов на косинус угла

между ними:

Слайд 17 Скалярное произведение векторов
Если , то

Скалярное произведение векторовЕсли , то , т.к.

, т.к.

.

Если , то , т.к. .

Если , то , т.к. .

Слайд 18 Пример 1.

Вычислить скалярное произведение векторов и

Пример 1.Вычислить скалярное произведение векторов и , если

, если ;

и .

Решение:

Слайд 19 Скалярное произведение векторов
Необходимое и достаточное условие перепендикулярности векторов
Скалярное

Скалярное произведение векторовНеобходимое и достаточное условие перепендикулярности векторовСкалярное произведение двух ненулевых

произведение двух ненулевых векторов равно нулю тогда и только

тогда, когда эти векторы ортогональны, т.к. и наоборот.

Слайд 20 Свойства скалярного произведения
Коммутативность:
Ассоциативность:
Дистрибутивность относительно суммы векторов:
Скалярное

Свойства скалярного произведенияКоммутативность: Ассоциативность: Дистрибутивность относительно суммы векторов:Скалярное произведение двух ненулевых

произведение двух ненулевых векторов равно нулю тогда и только

тогда, когда эти векторы ортогональны.

Слайд 21 Угол между векторами
Так как

Угол между векторамиТак как

, то угол между векторами можно вычислять по формуле:

Слайд 22

Слайд 23 Рене Декарт предложил координатный метод
Метод позволяет описывать геометрические

Рене Декарт предложил координатный методМетод позволяет описывать геометрические объекты аналитически, т.е. на языке алгебры.

объекты аналитически, т.е. на языке алгебры.

Слайд 24 Одномерная система координат
Прямая с заданным направлением
Задана точка –

Одномерная система координатПрямая с заданным направлениемЗадана точка – начало координатВыбран единичный масштаб

начало координат
Выбран единичный масштаб

Слайд 25 Координата точки
Координата точки равна расстоянию от начала координат

Координата точкиКоордината точки равна расстоянию от начала координат до заданной точкиКоордината

до заданной точки
Координата положительна, если направление вектора

совпадает с направлением координатной оси
Иначе координата точки отрицательна

Слайд 26 Двумерная система координат

Двумерная система координат

Слайд 27 Трёхмерная система координат

Трёхмерная система координат

Слайд 28 Правая система координат
Левая система координат

Правая система координатЛевая система координат

Слайд 29 Расстояние между точками на прямой линии

Расстояние между точками на прямой линии

Слайд 30 Расстояние между точками на плоскости

Расстояние между точками на плоскости

Слайд 31 Расстояние между точками в геометрическом пространстве

Расстояние между точками в геометрическом пространстве

Слайд 32

Слайд 33

Слайд 34

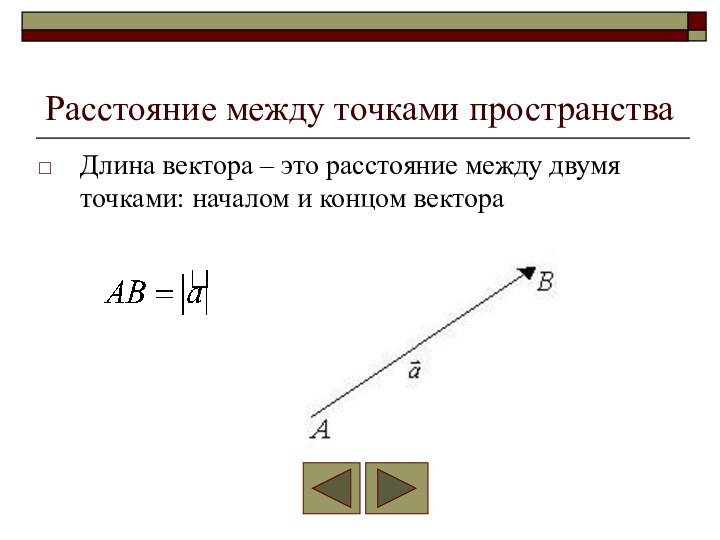
Слайд 35 Расстояние между точками пространства
Длина вектора – это расстояние

Расстояние между точками пространстваДлина вектора – это расстояние между двумя точками: началом и концом вектора

между двумя точками: началом и концом вектора

Слайд 36 Расстояние между точками пространства
Из определения скалярного произведения следует,

Расстояние между точками пространстваИз определения скалярного произведения следует, что

что

, т.к. cos0=1.
Следовательно, . (расстояние между 2-я точками)

Вывод. Длину вектора можно найти с помощью операции скалярного произведения. В этом случае говорят, что в линейном векторном пространстве геометрических векторов введена метрика, т.е. способ вычисления расстояний между точками этого пространства.

Слайд 37 Свойства длины вектора
1.
2.

Свойства длины вектора 1. 2. ,

,

 - вещественное число
3. - неравенство Коши- Буняковского
4. - неравенство треугольника

Слайд 38 Пример 3.

Вычислить длину вектора

Пример 3.Вычислить длину вектора , если

, если

и

Решение:

,

Слайд 39 Ортонормированный базис

Ортонормированный базис

Слайд 40 Пример 4.
Известны координаты начальной и конечной точек вектора

Пример 4.Известны координаты начальной и конечной точек вектора : A(1, 3,

: A(1, 3, -2)

и B(-1, 2, 7).
Разложить вектор по базису , , .
Решение. В примере 1 были найдены координаты вектора (-2; -1; 9).
Следовательно =-2 - +9
Ответ: =-2 - +9

Слайд 41 Пример 2.
Известны координаты начальной и конечной точек вектора

Пример 2.Известны координаты начальной и конечной точек вектора : A(1, 3,

: A(1, 3, -2)

и B(-1, 2, 7).
Разложить вектор по базису , , .
Решение. В примере 1 были найдены координаты вектора (-2; -1; 9).
Следовательно =-2 - +9
Ответ: =-2 - +9

  • Имя файла: analiticheskaya-geometriya.pptx
  • Количество просмотров: 119
  • Количество скачиваний: 0
- Предыдущая Am, is или are? Использование глагола to be
Следующая - Илиада

Похожие презентации

Управление сетями связи в стандарте GSM. Стандартные интерфейсы в системе сетевого управления GSM Управление сетями связи в стандарте GSM. Стандартные интерфейсы в системе сетевого управления GSM 133
The quiz The quiz 101
Словарь архаизмов презентация к уроку Словарь архаизмов презентация к уроку 119
Презентация по развитию речи на тему Что?Где?Когда?(3 класс) Презентация по развитию речи на тему Что?Где?Когда?(3 класс) 122
Масленица Масленица 68
ИННОВАЦИОННАЯ ИНФРАСТРУКТУРА УРАЛЬСКОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА ИННОВАЦИОННАЯ ИНФРАСТРУКТУРА УРАЛЬСКОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА 144
Презентация Презентация 87
Формирование рефлексивной самооценки как условие сохранения и укрепления психологического здоровья учащихся (3 класс) учебно-методический материал (3 класс) Формирование рефлексивной самооценки как условие сохранения и укрепления психологического здоровья учащихся (3 класс) учебно-методический материал (3 класс) 51
ПРЕЗЕНТАЦИЯ Из опыта работы УЧИТЕЛЯ НАЧАЛЬНЫХ КЛАССОВ СКНАРОВСКОЙ ООШ. Чухлебовой Татьяны Владимировны ЧАСТЬ2 материал ПРЕЗЕНТАЦИЯ Из опыта работы УЧИТЕЛЯ НАЧАЛЬНЫХ КЛАССОВ СКНАРОВСКОЙ ООШ. Чухлебовой Татьяны Владимировны ЧАСТЬ2 материал 127
Сенсорная коробочка: Морское дно учебно-методическое пособие (младшая группа) Сенсорная коробочка: Морское дно учебно-методическое пособие (младшая группа) 130
бирки на пластилин бирки на пластилин 130
Методы интенсификации добычи нефти Методы интенсификации добычи нефти 139
Конспект НОД по конструированию для детей средней (старшей) группы Дом, в котором я живу план-конспект занятия по конструированию, ручному труду (средняя, старшая группа) Конспект НОД по конструированию для детей средней (старшей) группы Дом, в котором я живу план-конспект занятия по конструированию, ручному труду (средняя, старшая группа) 227
Адаптация детей в детском саду презентация к уроку (младшая группа) Адаптация детей в детском саду презентация к уроку (младшая группа) 107
Предметно – пространственная среда по развитию языковой способности дошкольников презентация Предметно – пространственная среда по развитию языковой способности дошкольников презентация 123
Қарағанды мемлекеттік медицина университетиБиохимия кафедрасы Қарағанды мемлекеттік медицина университетиБиохимия кафедрасы 100
ПК 4.5.Участвовать в исследовательской и проектной деятельности, внедрять в практику новые образовательные технологии под руководством. проект (4 класс) ПК 4.5.Участвовать в исследовательской и проектной деятельности, внедрять в практику новые образовательные технологии под руководством. проект (4 класс) 94
Тема: Электрическая энергия проект (подготовительная группа) Тема: Электрическая энергия проект (подготовительная группа) 101
Конспект познавательно - исследовательской образовательной деятельности с детьми старшего возраста. Тема: Умные капельки. план-конспект занятия (старшая группа) Конспект познавательно - исследовательской образовательной деятельности с детьми старшего возраста. Тема: Умные капельки. план-конспект занятия (старшая группа) 38
Рекомендации для родителей Расскажите детям о космосе презентация к уроку (младшая группа) Рекомендации для родителей Расскажите детям о космосе презентация к уроку (младшая группа) 158
fotootchyot fotootchyot 119
Джеки Чан Джеки Чан 113
Презентация к классному часу : Я талантлив. презентация к уроку (3 класс) Презентация к классному часу : Я талантлив. презентация к уроку (3 класс) 115
Электрический ток в вакууме Электрический ток в вакууме 103
Фигуры undertale Фигуры undertale 119
Понятие правосудия Понятие правосудия 134
Cтроительные машины для уплотнения строительных смесей Cтроительные машины для уплотнения строительных смесей 98
Воздухоочиститель трактора Воздухоочиститель трактора 141
Файлняфки №1 Файлняфки №1 85
У школьного порога консультация (подготовительная группа) У школьного порога консультация (подготовительная группа) 116