Презентация на тему Аппаратные методы ускорения умножения

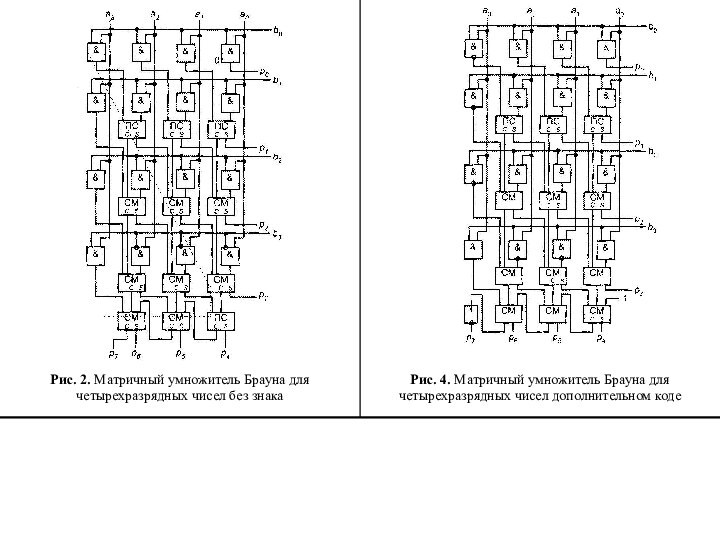
– с матричной структурой; б – со структурой двоичного

дерева

Древовидные умножители включают в себя три степени:
ступень формирования битов ЧП, состоящую из n2 элементов «&»;
ступень сжатия частичных произведений – реализуется в виде дерева параллельных сумматоров(накопителей), служащего для сведения частичных произведений в вектору сумм и вектору переносов;
ступень заключительного суммирования, где осуществляется сложение вектора сумм и вектора переносов с целью получения конечного результата.

На сегодня наибольшее распространение получили три древовидных схемы суммирования ЧП:
дерево Уоллеса;
дерево Дадда;
перевернутое ступенчатое дерево.

« Дерево Уоллеса – это оператор с n входами и log2n выходами, в котором код на выходе равен числу единиц во входном коде. »

(вариант 1) : а – логика суммирования; б –

точечная диаграмма

Рис. 7. Умножитель 4х4 со структурой дерева Уоллеса

Рис. 8. Суммирование ЧП с помощью дерева Уоллеса (вариант 2) :
а – логика суммирования; б – точечная диаграмма

высоты промежуточных матриц 29,19,13,9,6,4,3 и 2.
На рис. 9

описан умножитель 4x4, реализующий алгоритм дерева Дадда. Для этого требуется 16 схем «&», два полусумматора, четыре полных сумматора и шестиразрядный сумматор. Схема содержит три ступени с высотами промежуточных матриц: 4,3 и 2. На этапе суммирования вектора сумм и вектора переносов необходим (2n - 2)-разрядный сумматор.

Рис. 9. Суммирование ЧП с помощью дерева Дадда чисел без знака: а – логика суммирования; б – точечная диаграмма

к матричному умножителю, может быть адаптирована и для умножителя

со схемой Дадда. В таком случае схема сжатия приобретает вид, показанный на рис. 10.

Рис. 10. Суммирование ЧП с помощью дерева Дадда в дополнительном коде : а – логика суммирования; б – точечная диаграмма

Различия методов Уоллеса и Дадда являются следствием разных подходов к решению задачи "компрессии" суммирования. Алгоритм Уоллеса ориентирован на сжатие кодов как можно раньше, на самых ранних этапах, а алгоритм Дадда стремится это сделать по возможности позже, то есть наибольший уровень сжатия относит к завершающим стадиям.
Сравнивая схемы Уоллеса и Дадда, можно отметить, что число каскадов сжатия в них одинаково, однако количество используемых полусумматоров и полных сумматоров в схеме Дадда меньше (при подсчете числа элементов обычно не учитывают многоразрядные сумматоры, предназначенные для окончательного сложения векторов сумм и переносов). С другой стороны, на этапе сложения векторов сумм и переносов в варианте Уоллеса требуется сумматор с меньшим числом разрядов.
У обеих схем имеется общий недостаток — нерегулярность структуры, особенно у дерева Уоллеса.