Презентация на тему Asymptotes of graphs

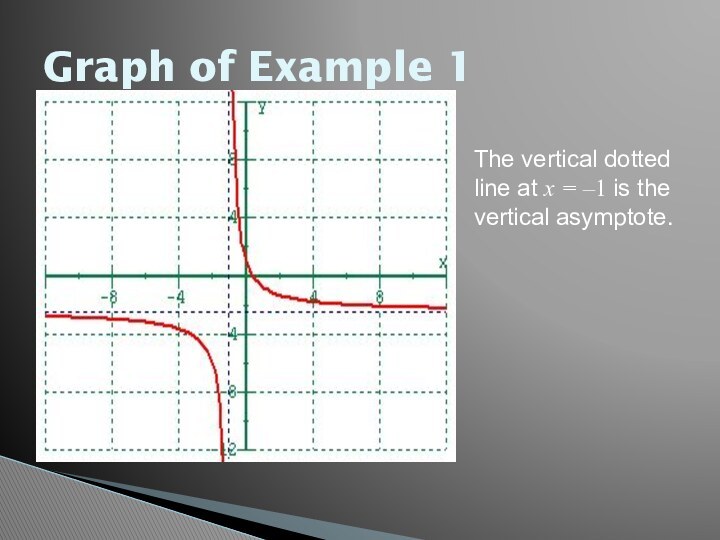
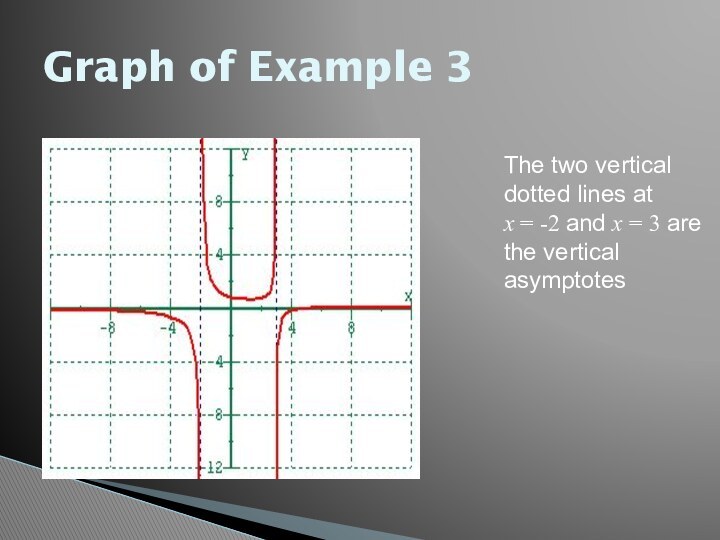
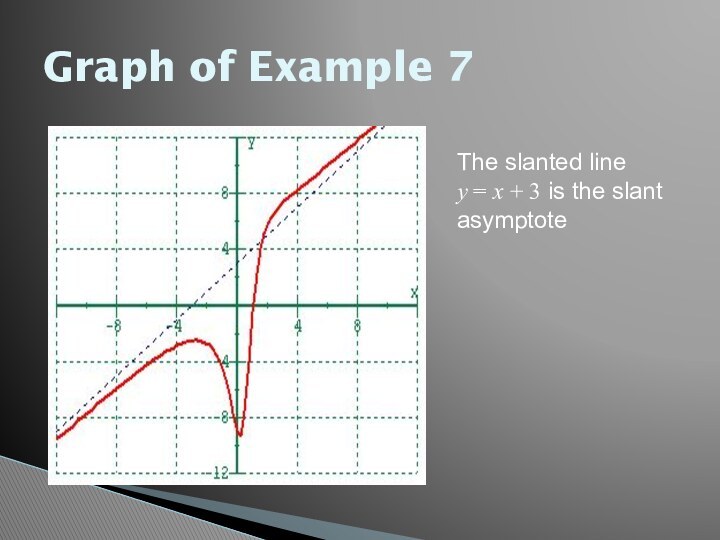
for a graph of f(x).
F(x) gets closer and closer

to the asymptote as it approaches either a specific value a or positive or negative infinity.
The functions most likely to have asymptotes are rational functions

Definition of an Asymptote

The denominator of the simplified

rational function is equal to 0.
The simplified rational
function may have cancelled factors
common to both the numerator and
denominator.

Vertical Asymptotes

Let denominator (2+2x) = 0


Vertical asymptote

x = –1 is the vertical asymptote.

denominator

2. Cancel any
Common factors.

x = 3 is the vertical asymptote

to cancel.
Factorise

g(x) has two vertical asymptotes

x = -2 and x = 3

Denominator = 0

at
x = -2 and x = 3 are

the vertical asymptotes

Denominator (D)

1) Degree N < Degree D Horizontal Asymptote: y=0

2) Degree N = Degree D  Horizontal Asymptote: y= Co-eff. of
leading ‘x’

3) Degree N > Degree D  Horizontal Asymptote: y = slant or
DNE

Horizontal Asymptotes

Degree N < Degree D
(x → ∞ and

x → -∞)
horizontal line y = 0

N

D

0 is the horizontal asymptote.

Degree N = Degree D
Horizontal asymptote: y=6/5.

Note: 6 and 5 are leading coefficients
(x→∞ and as x→-∞)
line y=6/5

y = 6/5 is the horizontal asymptote.

No horizontal asymptote
Degree N > Degree

D

N is one bigger than Degree D.
Use long division:

divide N by D

N

D

Use the quotient:

The slant asymptote is:

x + 3 is the slant asymptote

asymptotes for each of the following functions.