- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Дифференциальные уравнения
Содержание
- 2. Дифференциа́льное уравне́ние — уравнение, связывающее значение производной
- 3. Первоначально дифференциальные уравнения возникли из задач механики,
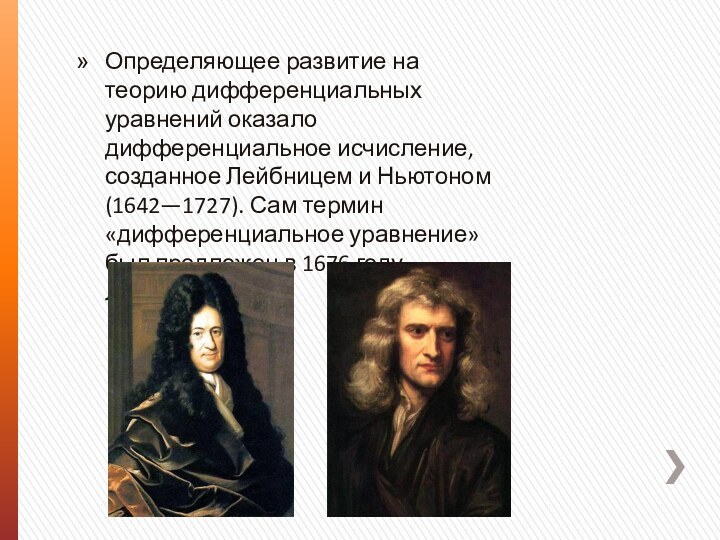
- 4. Определяющее развитие на теорию дифференциальных уравнений оказало
- 5. Основным аналитическим достижением Ньютона было разложение всевозможных
- 6. Из огромного числа работ XVIII века по
- 7. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙДифференциальные уравнения находят широчайшее применение
- 8. Начало качественной теории дифференциальных уравнений было положено
- 9. Скачать презентацию
- 10. Похожие презентации
Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут