Слайд 2
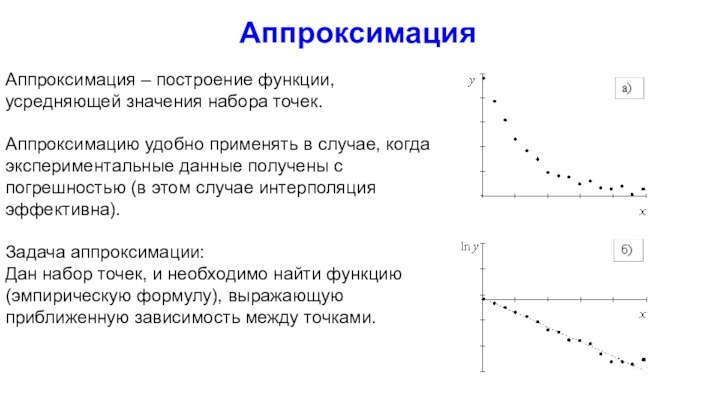
Метод наименьших квадратов
Оптимальные параметры эмпирической функции находятся из
соотношения:
Эмпирическая формула
Отклонение эмпирической формулы от экспериментальных данных
Среднеквадратичное отклонение эмпирической
формулы от экспериментальных данных
т.е.
где
Слайд 3
Применение метода наименьших квадратов
Разделив все слагаемые в уравнениях
(n+1) получим:
Обозначим:
Получим:
Слайд 4
Исследование операций
Исследование операций (ИСО) — применение математических, количественных методов
для обоснования решений во всех областях целенаправленной человеческой деятельности.
Цель исследования операций — предварительное количественное обоснование оптимальных решений с опорой на показатель эффективности.
Исследование операций (ИСО) -
это наука о количественном обосновании оптимальных решений на основе построения и использования математической модели.
Слайд 5
Основные понятия модели исследования операций
Целевая функция
Функция ограничения
Внутренние параметры
Оптимизационная
модель (модель с целевой функцией)
Неоптимизационная модель (модель без целевой
функцией)
Метод оптимизации (метод исследования операций)
Оптимальное решение
Слайд 6
Разделы дисциплины исследования операций
Математическое программирование ("планирование") - методы отыскания экстремальных

значений функции, на аргументы которой наложены ограничения.
Линейное программирование (ЛП) –
задачи с линейными целевыми функциями и ограничениями.
Нелинейное программирование (НП) рассматривает задачи с нелинейными целевыми функциями и ограничениями.
Целочисленное линейное программирование – решение задач, у которых все или некоторые переменные должны принимать целочисленные значения.
Динамическое программирование выбор наиболее оптимального управления динамическим объектом во времени.
Аппарат теории вероятностей позволяет находить оптимальные параметры стохастических систем (СМО, регрессионный и корреляционный анализ и т.п.).
Теория игр и принятия решений рассматривает процессы выбора наилучшей из нескольких альтернатив в ситуациях определенности, в условиях риска (данные можно описать с помощью вероятностных распределений), в условиях неопределенности (вероятностное распределение либо неизвестно, либо не может быть определено).
Теория нечетких множеств позволяет производить оценку нечетких данных и нечетких суждений (например, с помощью этого аппарата можно оценивать субъективное мнение экспертов.
Слайд 7
Одна задача линейного программирования
Задача:
Для окраски помещения необходимо купить
15 кг краски. Эту краску
можно купить в банках двух
типов: по 1,5 кг, стоимостью 10 рублей каждая, или банках весом 0,9 кг, стоимостью 8,5 рублей. Для перевозки используется ящик, в который может уместиться 8 банок первого типа или 25 банок второго типа.
Решение:
x1 - количество банок первого типа (каждая банка занимает 1/8 ящика),
x2 - количество банок второго типа (каждая банка занимает 1/25 ящика).
1,5x1+ 0,9x2 >= 15
1/8x1+ 1/25x2 <= 1
Стоимость покупки: L=10x1+8,5x2 -> min
Слайд 8
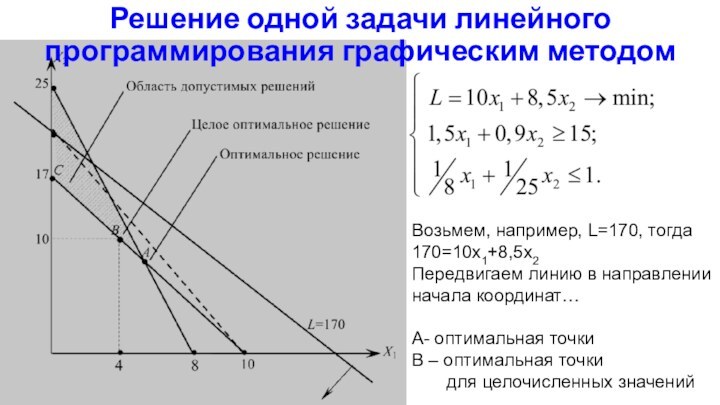
Решение одной задачи линейного программирования графическим методом
Возьмем, например,
L=170, тогда
170=10x1+8,5x2
Перeдвигаем линию в направлении
начала координат…
A- оптимальная точки
В –
оптимальная точки
для целочисленных значений
Слайд 9
Решение одной задачи линейного программирования
Найдем точку А из
уравнения
x1=5,8; x2=7,1; L3=118,35
Округление x1=6, x2=7 не является допустимым
решением
Допустимым является решение x1=4, x2=10, L=125
Слайд 10
Еще одна задача линейного программирования
Имеются четыре вида продуктов
П 1 , П 2 , П 3 ,
П 4 . Известна стоимость каждого продукта с 1 , с 2 , с 3 , с 4 . В рационе должно быть белков не менее b 1 ; жиров не менее b 2 ; углеводов не менее b 3 . Известно удельное содержание каждого вещества в единице продукта. Необходимо рассчитать рацион, содержащий необходимое количество полезных веществ и при этом, чтобы стоимость всего рациона была минимальной. Построим математическую модель:
j – номер продукта ; i – номер вещества;
aij – удельное количество в j – м продукте i – го вещества
Слайд 11
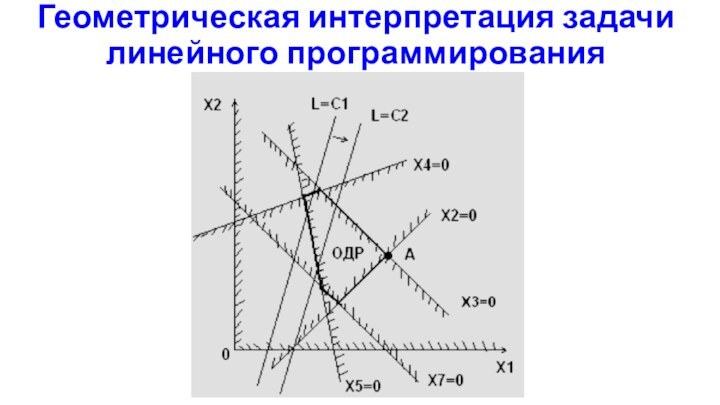
Геометрическая интерпретация задачи линейного программирования
Слайд 12
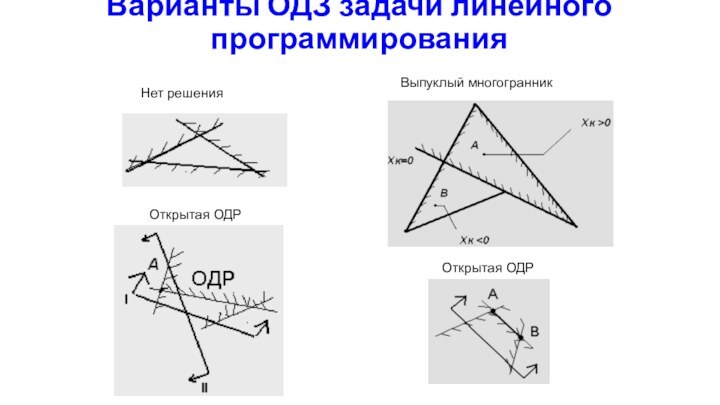
Варианты ОДЗ задачи линейного программирования
Нет решения
Выпуклый многогранник
Открытая ОДР
Открытая
ОДР
Слайд 13
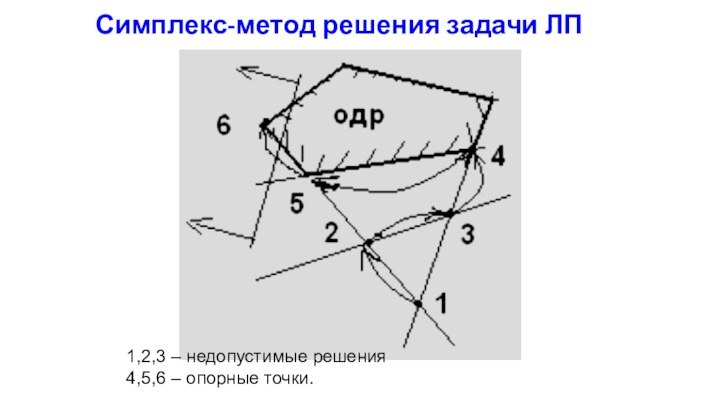
Симплекс-метод решения задачи ЛП
1,2,3 – недопустимые решения
4,5,6 –
опорные точки.
Слайд 14
Формы записи системы уравнений для ЛП
• Система уравнений
и ограничений
• Каноническая.
• Матричная.
Слайд 15
Система уравнений и ограничений
Слайд 16
Таблица приёмов перевода системы управлений к каноническому виду
Слайд 17
И еще одна задача линейного программирования
На складе фирмы
имеется 50 ед. (погонных метров, квадратных футов или иных
подходящих единиц измерения) дерева и 54 ед. (возможно, других) металла. Из этого сырья можно производить дачную мебель двух видов: столы и стулья. Пусть для изготовления одного стола требуется 10 ед. дерева и 6 ед. металла, а для изготовления одного стула — 5 ед. дерева и 9 ед. металла. Продажная цена одного стола составляет 8 условных денежных единиц, а одного стула — 6 у. е.
Спрашивается, какое количество столов и стульев следует изготовить, чтобы максимизировать доход, уложившись при этом в имеющиеся ресурсы?
Слайд 18
Представление задачи ЛП в каноническом виде
x1 - количество
производимых столов;
X2 – количество производимых стульев;
Целевая функция:
L(x1, x2)
= 8x1 + 6x2 + x3 + x4 —> max, =>
L(x1, x2) = -8x1 - 6x2 - x3 - x4 —> min
10x1 + 5х2 + x3 + x4 = 50,
6x1 + 9x + x3 + x4 = 54.
x1>=0, x2 >=0, x3 >=0, x4 >=0.
Слайд 19
Представление задачи ЛП в матричном виде
x1 - количество
производимых столов;
X2 – количество производимых стульев;
Целевая функция:
L(x1, x2)
= 8x1 + 6x2 + x3 + x4 —> max, =>
L(x1, x2) = -8x1 - 6x2 - x3 - x4 —> min
10, 5, 0, 0
6, 9, 0, 0
P0=(50,54,0,0)T
x1>=0, x2 >=0, x3 >=0, x4 >=0.
Слайд 20
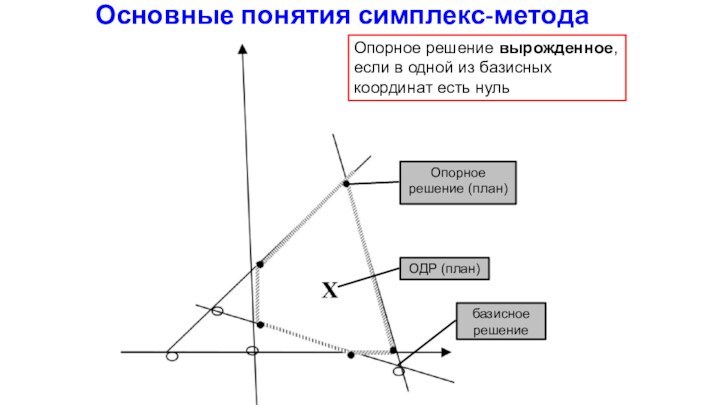
Основные понятия симплекс-метода
Опорное решение (план)
базисное решение
Опорное решение вырожденное,
если в одной из базисных координат есть нуль
ОДР (план)
Слайд 21
Схема симплекс-метода
Система уравнений записывается в канонической форме
Строится исходных
опорный план:
Проверка текущего плана на оптимальность
Все оставшиеся вектора
разлагаются по базису, вычисляется целевая функция для них, выбирается для включения тот вектор, при котором целевая функция наименьшая
4. Вектор для исключения из базиса выбирается по формуле
5. Изменение базиса с помощью преобразований Жордана.
Слайд 22
Пример решения задачи ЛП с помощью симплекс-метода (1)
Задача:
Слайд 23
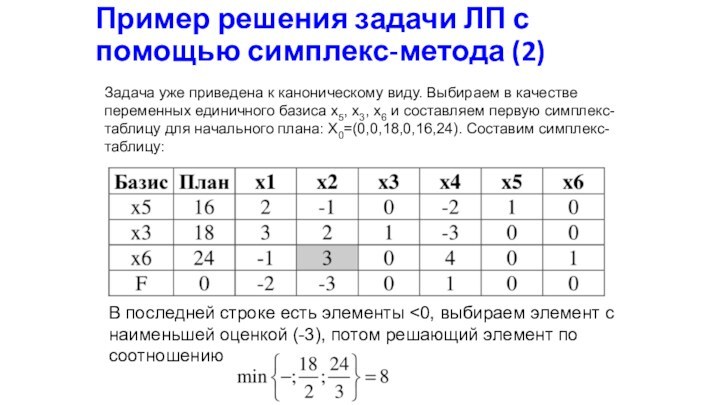
Пример решения задачи ЛП с помощью симплекс-метода (2)
Задача
уже приведена к каноническому виду. Выбираем в качестве переменных
единичного базиса x5, x3, x6 и составляем первую симплекс-таблицу для начального плана: X0=(0,0,18,0,16,24). Составим симплекс-таблицу:
В последней строке есть элементы <0, выбираем элемент с наименьшей оценкой (-3), потом решающий элемент по соотношению
Слайд 24
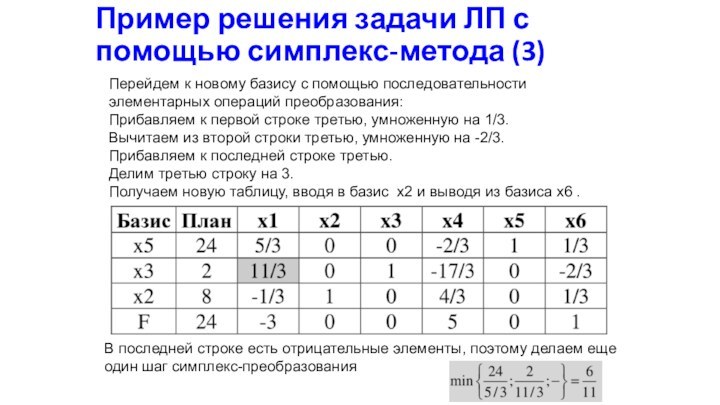
Пример решения задачи ЛП с помощью симплекс-метода (3)
Перейдем
к новому базису с помощью последовательности элементарных операций преобразования:
Прибавляем
к первой строке третью, умноженную на 1/3.
Вычитаем из второй строки третью, умноженную на -2/3.
Прибавляем к последней строке третью.
Делим третью строку на 3.
Получаем новую таблицу, вводя в базис x2 и выводя из базиса x6 .
В последней строке есть отрицательные элементы, поэтому делаем еще один шаг симплекс-преобразования
Слайд 25
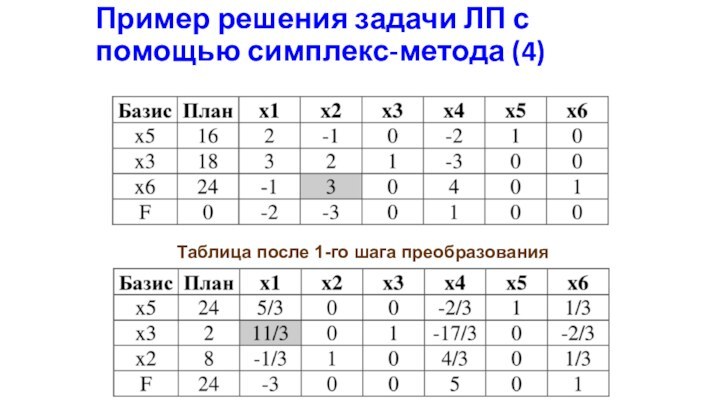
Пример решения задачи ЛП с помощью симплекс-метода (4)
Таблица
после 1-го шага преобразования
Слайд 26
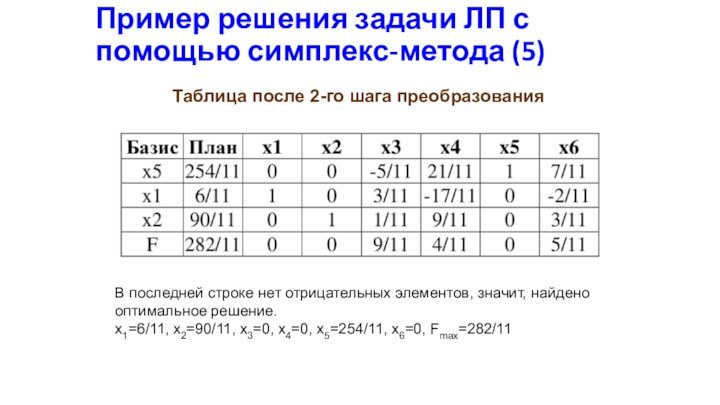
Пример решения задачи ЛП с помощью симплекс-метода (5)
В
последней строке нет отрицательных элементов, значит, найдено оптимальное решение.
x1=6/11,
x2=90/11, x3=0, x4=0, x5=254/11, x6=0, Fmax=282/11
Таблица после 2-го шага преобразования
Слайд 27
Нелинейное программирование (НП)
Слайд 28
Постановка задачи нелинейного программирования
Слайд 29
Постановка задачи нелинейного программирования
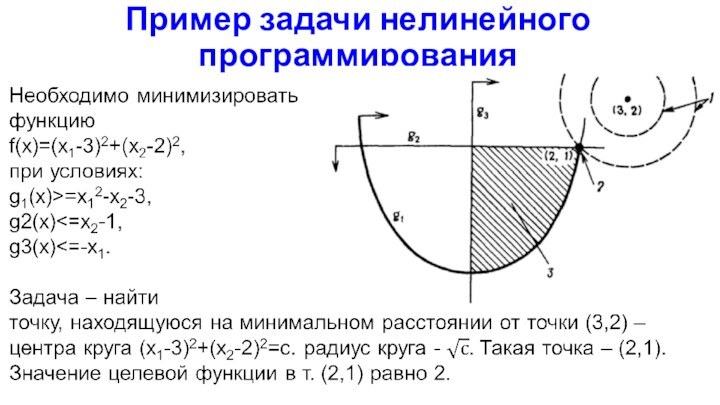
Необходимо минимизировать (максимизировать) f(x1,x2,..,xn) при
ограничениях:
где функции
нелинейны.
Слайд 30
Пример задачи нелинейного программирования
Слайд 31
Классификация методов нелинейного программирования
По количеству локальных критериев в
целевой функции методы делятся на:
однокритериальные,
многокритериальные.
По длине вектора переменных делятся
на:
однопараметрические или одномерные (n=1),
многопараметрические или многомерные (n>1).
По наличию ограничений:
без ограничений (безусловная оптимизация),
с ограничениями (условная оптимизация).
По типу информации, используемой в алгоритме поиска экстремума:
методы прямого поиска, т.е. методы, в которых при поиске экстремума целевой функции используются только ее значения;
градиентные методы первого порядка, в которых при поиске экстремума функции используются значения ее первых производных;
градиентные методы второго порядка, в которых при поиске экстремума функции наряду с первыми производными используются и вторые производные.
Слайд 32
Разделы в теории нелинейного программирования
выпуклое программирование (исследование выпуклых
и вогнутых функций),
квадратичное программирование (линейные ограничения и квадратичная целевая
функция),
целочисленное программирование (неизвестные параметры могут принимать только целочисленные значения),
стохастическое программирование (параметры принимают случайные значения, подчиняющиеся теории вероятности),
динамическое программирование (время содержится как параметр) и др.
Слайд 33
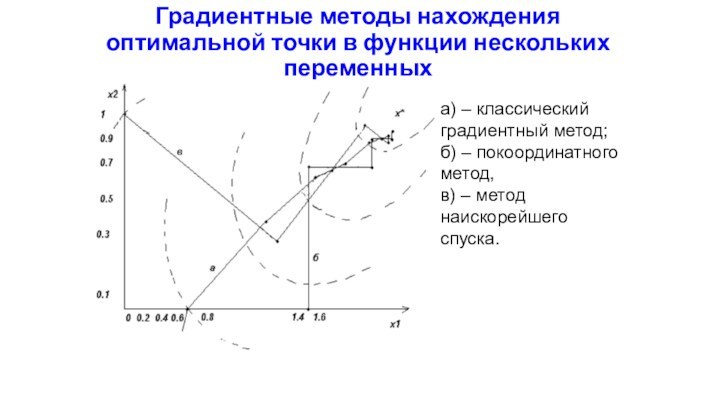
Градиентные методы нахождения оптимальной точки в функции нескольких
переменных
а) – классический градиентный метод;
б) – покоординатного метод,
в) –
метод наискорейшего спуска.
Слайд 34
Метод циклического изменения переменных
Представляет собой процедуру рекурсивного перебора
на множестве направлений поиска: каждый раз меняется только одна
переменная. Затем вдоль каждого из координатных направлений последовательно проводится поиск точки экстремума на основе методов одномерной минимизации. Однако, если линии уровня ЦФ имеют овражный характер, то процедура поиска становится неэффективной и даже может привести к отсутствию сходимости к точке локального экстремума, если изменение координатных направлений поиска осуществляется в циклическом порядке (показано Пауэллом).
Слайд 35
Классический градиентный метод
В качестве направления для изменения текущей
точки выбирается вектор, направление которого противоположно направлению вектора градиента
функции f(x).
Вектор -grad f (X) = - f(X) называется антиградиентом и является направлением наиболее быстрого ее убывания.
Рекурсивное соотношение для поиска новой точки будет:
Xk+1=xk-kf(X),
где k – величина шага на к-ой итерации.
k=1,2,..,
Слайд 36
Метод наискорейшего спуска (метод Коши)
Если во время поиска
шаг не меняется, то такой способ называется градиентным
методом с дискретным шагом.
Процесс оптимизации на первых итерациях можно значительно ускорить, если λk выбирать из условия λk =min f(Xk + λSk), где для нахождения Sk используется любой метод одномерной оптимизации. Такой метод называется методом наискорейшего спуска.
Критерий остановки метода: ||f(Xk)|| <εk
Недостаток метода – критерий остановки удовлетворяет не только точке экстремума, но и седловой точке.
Слайд 37
Пример применения метода наискорейшего спуска(2)
Выполнение этого шага приведет
в точку:
Проверим критерий оптимальности:
Точность не достигнута, из точки
делаем шаг вдоль направления антиградиента
f(X2) = 3(1,116 – 1,008λ1)2 + (1,688-2,26λ1)2 - (1,116 – 1,008λ1)( 1,688-2,26λ1) - 4(1,116 – 1,008λ1)
f’(X2) = 11,76 – 6,12λ1 = 0
Получаем λ1 = 0.52
Слайд 38
Метод деформируемого многогранника Нелдера-Мида
Симплекс – многогранник в n-мерном
пространстве
Слайд 39
Динамическое программирование
Динамическое программирование (или динамическое планирование) представляет собой
особый математический аппарат, позволяющий осуществлять оптимальное планирование управляемых процессов.
Под «управляемыми» подразумеваются процессы, на ход которых мы можем в той или другой степени влиять. (Е.С. Вентцель)
Слайд 40
История динамического программирования
Динамическое программирование возникло и сформировалось в
1950–1953 гг. благодаря работам Ричарда Беллмана и его сотрудников.
Беллман (Bellman) Ричард Эрнест (1920-84) – американский математик. Первыми задачами, решаемыми с помощью динамического программирования были задачи управления запасами.
Слайд 41
Задача динамического программирования
Задачи динамического программирования укладываются в
следующую схему:
I. Имеется набор способов действий – допустимых управлений.
II.
Имеется целевая функция («прибыль», «убыток») S = S(u), где u пробегает допустимые управления.
Требуется выбрать управление, которому отвечает оптимальное значение целевой функции.
Слайд 42
Формализация задачи динамического программирования
Динамическая система (ДС) – такой
объект, который может развиваться.
Квазидинамическая система – система, которую можно
привести к динамической.
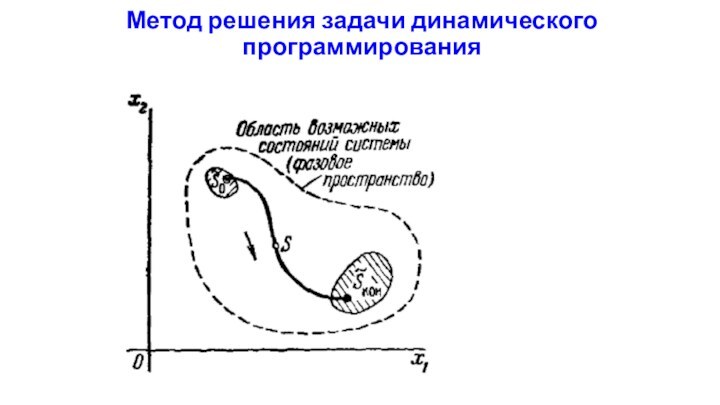
Пространство состояний (фазовое пространство) динамической системы – множество всех возможных состояний динамической системы.
ДС с дискретным временем – ДС, состояние которой меняется в дискретные моменты времени, например, t0, t1,t2,..,tn.
Траектория – набор состояний, через которые проходит ДС от начального к конечному состоянию.
Управляемая ДС – ДС, траекторию которой можно менять с помощью управляющих импульсов Uk.
Слайд 43
Функционирование динамической модели
1. В начальный момент времени t0
система находится в фиксированном состоянии 0.
2. Переход k-1
k от состояния в момент tk-1 к состоянию в момент tk (от t0 к t1 от t1 к t2 и т.д.) осуществляется под воздействие управляющих сигналов uk , т.е. k =(k-1 , uk). Набор состояний 0, 1 ,…, n – траектория ДС. Причем, начало всех траекторий одинаковое - 0.
Слайд 44
Общая задача динамического программирования
Пусть имеется управляемая динамическая система
оценивается каким-либо показателем, например, суммарным доходом S=S(u1,u2,..,un). Суммарный доход
равен сумме доходов на каждом шаге
S=f1+f2+…+fn. (1)
fk – доход на k-ом шаге, который зависит от состояния ДС в начале k-го шага и выбранного управления uk:
fk = fk(k-1 , uk) (2)
Подставляя (1) в (2) получим:
Такая функция называется аддитивной целевой функцией.
Слайд 45
Общая задача динамического программирования
Для анализа имеется управляемая динамическая
система, для которой выделено n шагов, а на каждом
шаге выделены все возможные состояния (k), через которые проходит система, а также выделено начальное состояние 0, а на каждом шаге заданы возможные управляющие воздействия (uk). Также имеется аддитивная функция.
Задача ДП состоит в том, чтобы найти такую последовательность управляющих воздействий во время функционирования ДС (u1,u2,…,un), чтобы аддитивная функция S достигала максимума или минимума. Траектория, на которой достигается max или min целевой функции, называется оптимальной траекторией. Задачей ДП является отыскание оптимальной траектории.
Слайд 46
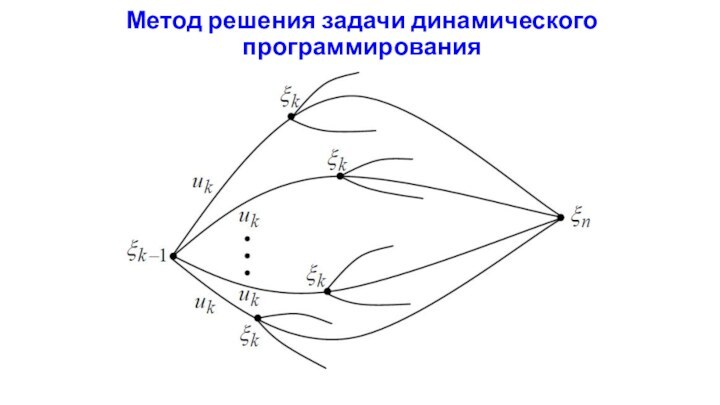
Метод решения задачи динамического программирования
Слайд 47
Метод решения задачи динамического программирования
Слайд 48
Метод решения задачи динамического программирования
Предположим, что к
на- чалу k-го шага система оказалась в состоянии k-1.
Оставшийся путь до конца система может проходить по различным траекториям в зависимости от выбора последующих управлений. Каждой траектории отвечает свой суммарный доход, т.е. доход на участке Обозначим этот доход через Sk.
Sk=fk+fk+1+…+fn
S*k(k-1) – условный максимальный доход – максимальный суммарный доход, начиная с k-го шага и до конца, т.е. на участке [k-1,n]. Тогда основную задачу ДП можно формализовать в виде:
И требуется найти условное оптимальное управление на k-м шаге u*k(k-1).
Слайд 49
Метод решения задачи динамического программирования
Задачи ДП решаются
в два этапа:
1. движение от конца к началу
Начиная
с кон- ца последовательно находим:
для всех возможных на соответствующих шагах состояний с использованием на каждом шаге, начиная с n-1-го, формулы для
Слайд 50
Метод решения задачи динамического программирования
Задачи ДП решаются
в два этапа:
1. движение от конца к началу
Начиная
с кон- ца последовательно находим:
для всех возможных на соответствующих шагах состояний с использованием на каждом шаге, начиная с n-1-го, формулы для
2 движение от начала к концу
Двигаясь от начала, существенно используя закрепленность начального состояния, строим безусловную оптимальную траекторию.
Слайд 52
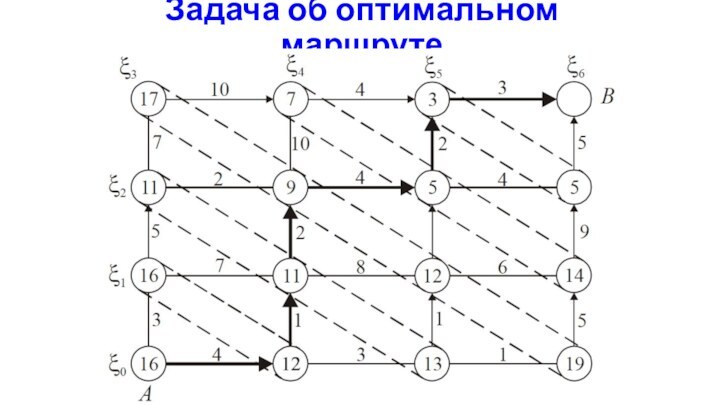
Задача об оптимальном маршруте
Требуется найти оптимальный маршрут
на плоскости, проходящий через некоторые точки.
ДС представляет собой
граф, где каждая вершина имеем четырех соседей. В нашем случае потребуется 6 шагов.
Состояние – узел графа. A – начальное состояние B – конечное состояние.
Под управлением будем понимать выбор направления движения: по горизонтали или вертикали.
Аддитивная целевая функция – величина потерь, приписанная к каждой дуге графа.
Целевая функция – суммарные потери на всех 6 шагах.
Решение:
Помечаем узлы графа последовательно от конца к началу минимальным весом, затем от начала к концу выбираем маршрут, с наименьшим весом для каждого шага.
Слайд 53
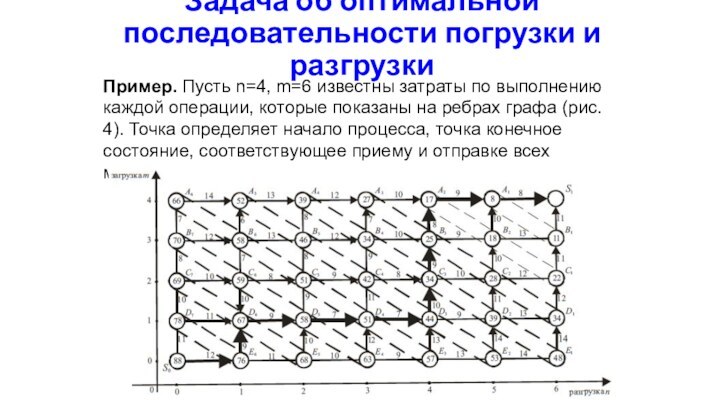
Задача об оптимальной последовательности погрузки и разгрузки
Пусть на
оптовую базу прибыло n машин с товаром для разгрузки
и m машин для загрузки товаров, направляемых в магазины. Материально ответственное лицо оптовой базы осуществляет оформление документов по операциям разгрузки или загрузки одной машины, а затем переходит к обслуживанию другой машины. Издержки от операций обусловлены простоем транспорта, типом операции (прием или отгрузка товара). Необходимо спланировать последовательность операций обоих видов таким образом, чтобы суммарные издержки по приему и отправке товаров для всех машин были минимальными.
Слайд 54
Задача об оптимальной последовательности погрузки и разгрузки
Если по
оси X отложить число n разгруженных машин, а по
оси Y число m загруженных товаром машин, то можно построить на плоскости граф состояний процесса, в котором каждая вершина характеризует состояние операции приема и отгрузки то- вара на оптовой базе. Ребра означают выполнение работы по приему или отправке товара на очередной машине. Каждому ребру можно сопоставить издержки, связанные с выполнением операции по разгрузке или загрузке машины.
Таким образом, задачи сводится к ранее рассмотренной задаче выбора оптимального маршрута.
Слайд 55
Задача об оптимальной последовательности погрузки и разгрузки
Пример. Пусть
n=4, m=6 известны затраты по выполнению каждой операции, которые
показаны на ребрах графа (рис. 4). Точка определяет начало процесса, точка конечное состояние, соответствующее приему и отправке всех машин.
Слайд 56
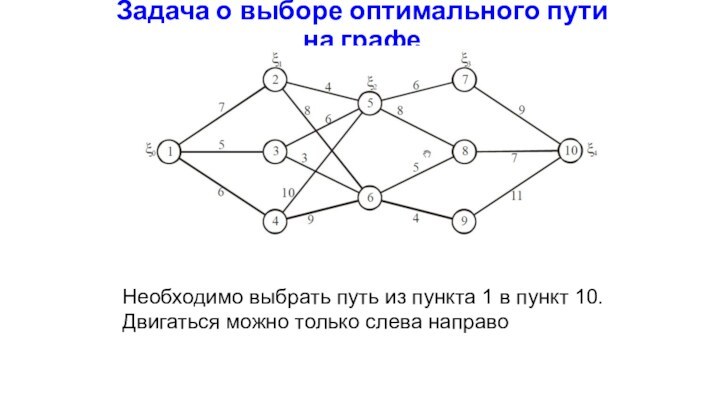
Задача о выборе оптимального пути на графе
Необходимо выбрать
путь из пункта 1 в пункт 10. Двигаться можно
только слева направо
Слайд 57
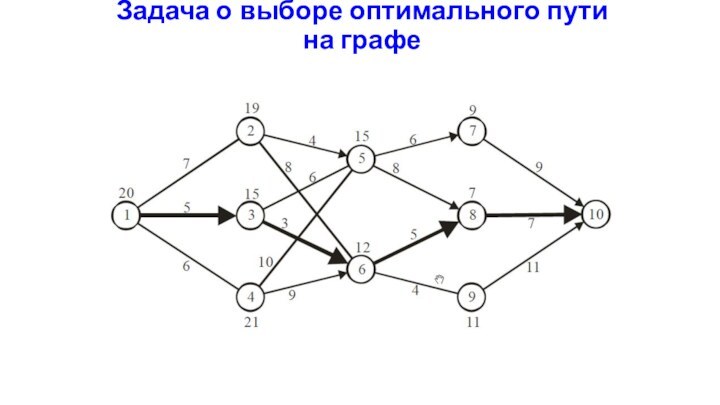
Задача о выборе оптимального пути на графе
Слайд 58
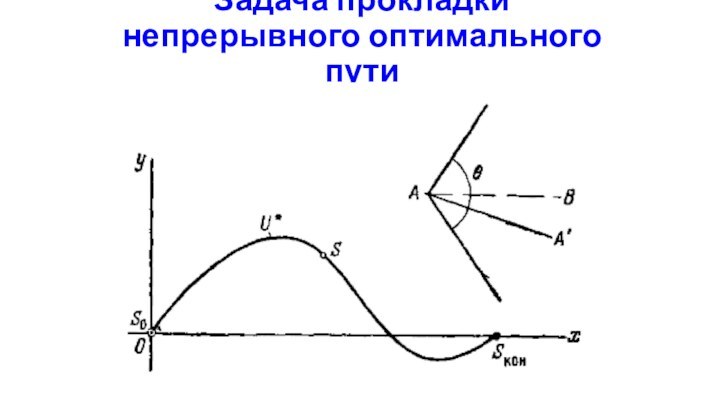
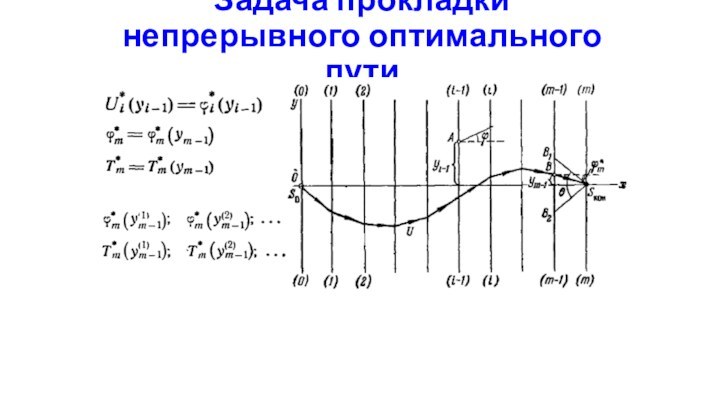
Задача прокладки непрерывного оптимального пути
Слайд 59
Задача прокладки непрерывного оптимального пути
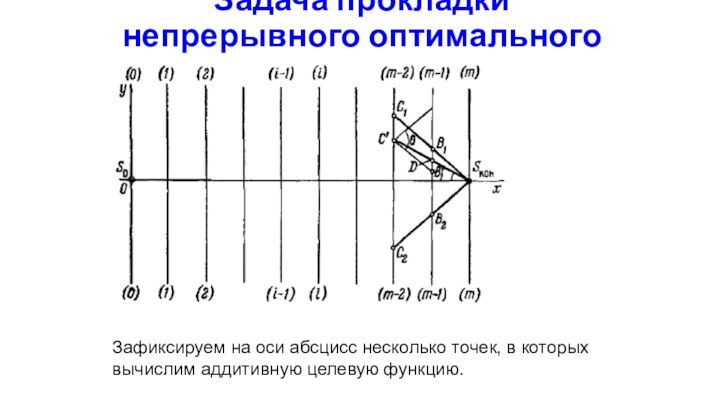
Слайд 60
Задача прокладки непрерывного оптимального пути
Зафиксируем на оси абсцисс
несколько точек, в которых вычислим аддитивную целевую функцию.
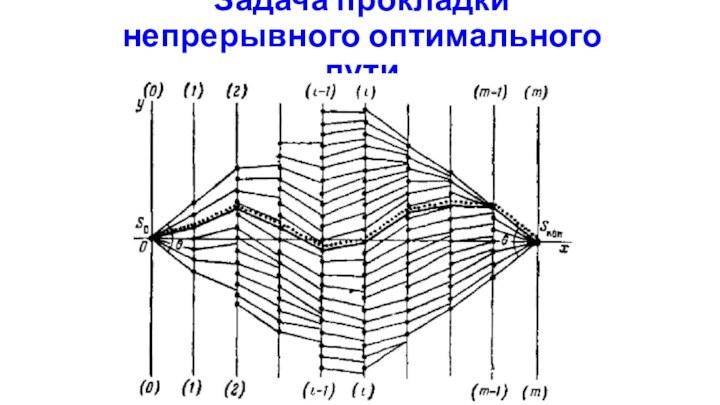
Слайд 61
Задача прокладки непрерывного оптимального пути
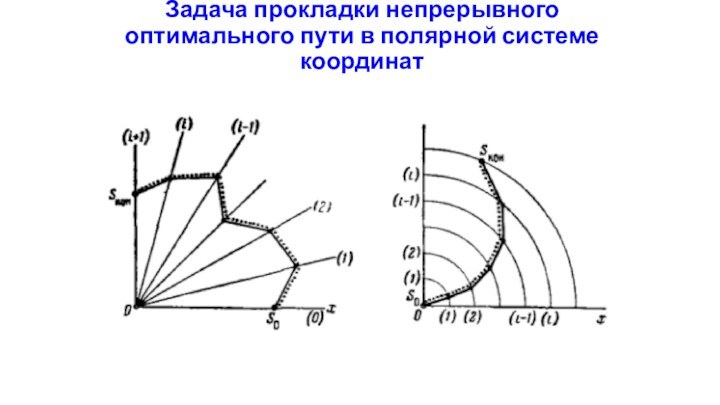
Слайд 62
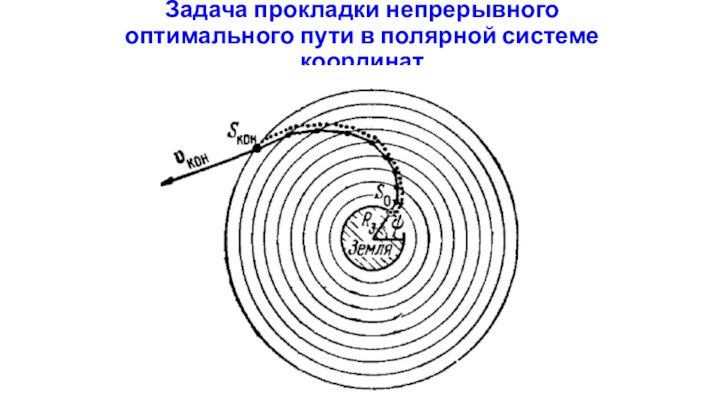
Задача прокладки непрерывного оптимального пути в полярной системе
координат
Слайд 63
Задача прокладки непрерывного оптимального пути в полярной системе
координат
Слайд 64
Задача о выборе оптимального оптимальной стратегии замены оборудования
Определить
оптимальные сроки замены оборудования в течение n лет, при
которых прибыль от эксплуатации оборудования максимальна, если известны: p – начальная стоимость оборудования; R(t) – стоимость производимой продукции на оборудовании возраста t лет; r(t) – ежегодные затраты на эксплуатацию оборудования возраста t лет; (t) – ликвидная стоимость оборудования возраста t лет. Предполагаются, что к началу планового периода оборудование является новым.
Слайд 65
Задача о выборе оптимального оптимальной стратегии замены оборудования
В
качестве управления будем использовать решение о замене или незамене
оборудования:
Слайд 66
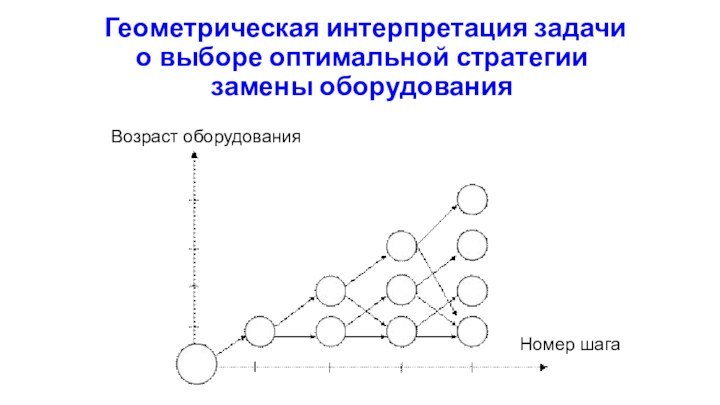
Геометрическая интерпретация задачи о выборе оптимальной стратегии замены
оборудования
Возраст оборудования
Номер шага
Слайд 67
Задача о выборе оптимального оптимальной стратегии замены оборудования
Замена
оборудования p=40 у.е.
Слайд 68
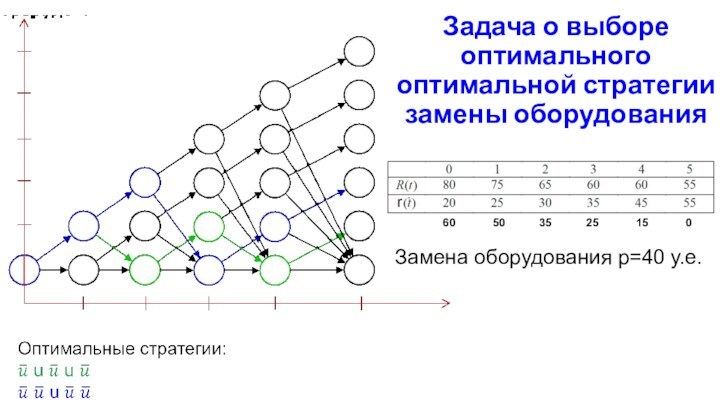
Задача о выборе оптимального оптимальной стратегии замены оборудования
Замена
оборудования p=40 у.е.
60 50
35 25 15 0
Слайд 69
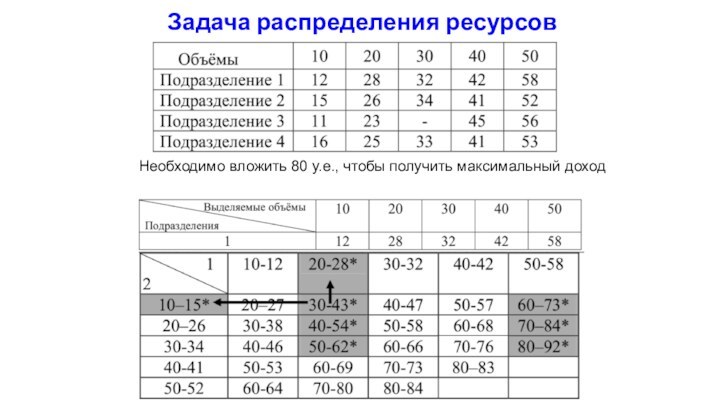
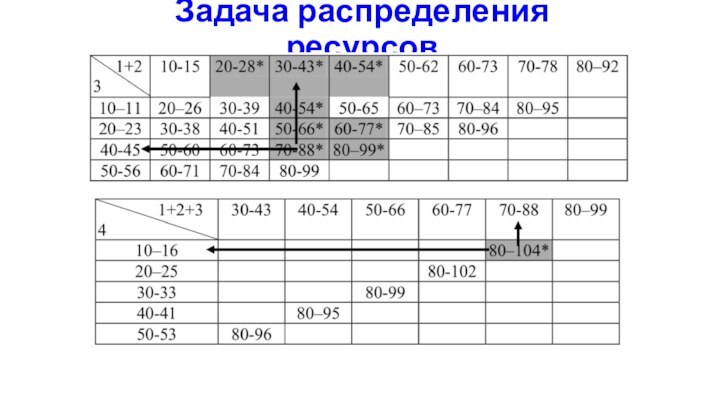
Задача распределения ресурсов
Необходимо вложить 80 у.е., чтобы получить
максимальный доход




















































![Автоматизация звука [т] в чистоговорках презентация к уроку (младшая, средняя, старшая, подготовительная группа)](/img/tmb/8/752503/cc320e1c8ac07df19f2e3dce0d0bef90-210x.jpg)


















