Слайд 2
Связность компонент
Граф G называется k-связным (k ≥1), если
не существует
набора из k-1 или меньшего числа узлов V`≤
V, такого, что
удаление всех узлов V` и инцидентных с ними ребер,
сделают граф G несвязанным.
Теорема Менгера: граф G является k-связанным тогда и
только тогда, когда любые два различные узла x и y графа G
соединены по крайне мере k путями, не содержащими
общих узлов (кроме x и y).
Для k существует алгоритм, отыскивающий k-связные
компоненты за линейное время по числу вершин и ребер.
Слайд 3
Точки сочленения
Пусть G = (V, Е) — связный
неориентированный граф.
Узел а называют точкой сочленения графа G,
если
существуют такие узлы v и w, что v, w и а различны и
всякий путь между v и w содержит узел а.
Иначе говоря, а — точка сочленения графа G, если
удаление узла a расщепляет G не менее чем на две
части.
Граф G называется двусвязным, если для любой
тройки различных узлов v, w, а существует путь между
V и w, не содержащий а.
Таким образом, неориентированный связный граф
двусвязен тогда и только тогда, когда в нем нет точек
сочленения.
Слайд 4
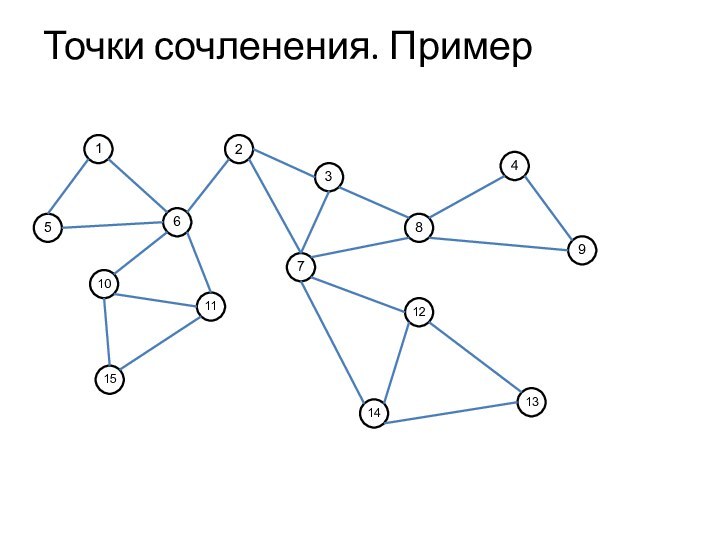
Точки сочленения. Пример
1
15
5
6
11
2
10
7
3
13
12
14
4
9
8
Слайд 5
Двусвязная компонента состоит из трех или более
его вершин,
в котором любые две вершины соединены, по
крайней мере, двумя
путями, не имеющими общих ребер.
Двусвязная компонента может представлять собой просто
две вершины, соединенные одним ребром.
Двусвязная компонента - устойчивая часть графа: если в ней удалить
вершину и все примыкающие к ней ребра, то любые две из оставшихся
вершин по-прежнему оказываются соединенными между собой.
Если граф, образованный компьютерами сети, двусвязен, то сеть
сохранит способность функционировать даже при выходе из строя
одного из компьютеров.
При планировании авиаперевозок двусвязные компоненты графа
гарантирует возможность переправить пассажиров по другому маршруту
при закрытии аэропорта по погодным условиям.
Слайд 6
Точки сочленения можно обнаружить с помощью грубой
силы, удаляя
из графа поочередно каждую вершину и
пользуясь одним из наших
алгоритмов обхода графа для
проверки связности оставшейся части. Если оставшийся граф
связен, то удаленная вершина не является точкой
сочленения.
При таком подходе мы должны выполнить n обходов графа с
n вершинами, что потребует O(n2) операций.
Однако сохраняя незначительное количество
дополнительной информации при обходе графов, можно
обнаружить все точки сочленения и компоненты
двусвязности при единственном обходе.
Слайд 7
Двусвязные компоненты
На множестве ребер графа G можно задать
естественное отношение, полагая, что для ребер е1 и e2
выполняется это отношение, если e1= e2 или они лежат на некотором цикле.
Легко показать, что это отношение является отношением эквивалентности, разбивающим множество ребер графа G на такие классы эквивалентности E1, Е2, . . ., Еk, что два различных ребра принадлежат одному и тому же классу тогда и только тогда, когда они лежат на общем цикле.
Для 1 i k обозначим через Vi множество узлов, лежащих на ребрах из Ei. Каждый граф Gi = (Vi, Ei) называется двусвязной компонентой графа G.
Слайд 8
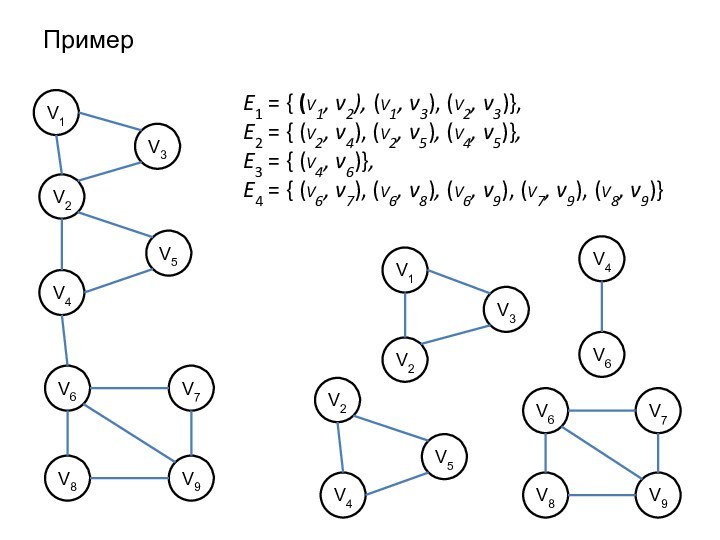
Пример
V1
V3
V2
V4
V5
V6
V7
V8
V9
V1
V3
V2
V2
V4
V5
V4
V6
V6
V7
V8
V9
E1 = { (v1, v2), (v1, v3), (v2,
v3)},
E2 = { (v2, v4), (v2, v5), (v4, v5)},
E3
= { (v4, v6)},
E4 = { (v6, v7), (v6, v8), (v6, v9), (v7, v9), (v8, v9)}
Слайд 9
Лемма 1.
Пусть Gi=(Vi, Ei) для 1
i k — двусвязные компоненты связного неориентированного графа
G = (V, Е).
Тогда
1) граф Gi двусвязен для каждого i, 1 i k;
2) для всех i j пересечение Vi Vj содержит не более одного узла;
3) а — точка сочленения графа G тогда и только тогда, когда а Vi Vj для некоторых i j.
Слайд 10
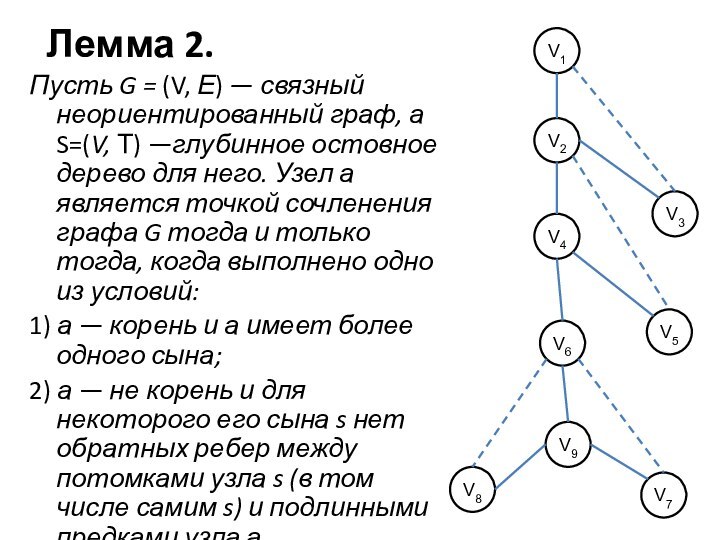
Лемма 2.
Пусть G = (V, Е) —
связный неориентированный граф, а S=(V, Т) —глубинное остовное дерево
для него. Узел а является точкой сочленения графа G тогда и только тогда, когда выполнено одно из условий:
1) а — корень и а имеет более одного сына;
2) а — не корень и для некоторого его сына s нет обратных ребер между потомками узла s (в том числе самим s) и подлинными предками узла а.
V1
V3
V2
V4
V5
V6
V7
V8
V9
Слайд 11
Нахождение двусвязных компонент и точек сочленения методом поиска
в глубину
Для всех вершин v вычисляются числа dfnumber[v]. Они
фиксируют последовательность обхода вершин глубинного остовного дерева в прямом порядке.
Для каждой вершины v вычисляется число
dfnumber[v];
low[v] = min dfnumber[z], (v, z) – обратное ребро;
low[x], x – потомок v.
3. Точки сочленения определяются следующим образом:
корень остовного дерева будет точкой сочленения тогда и только тогда, когда он имеет двух и более сыновей;
вершина v, отличная от корня, будет точкой сочленения тогда и только тогда, когда имеет такого сына w, что
low[w] dfnumber [v].
Слайд 12
Алгоритм нахождения двусвязных компонент и точек сочленения
Вход. Связный
неориентированный граф G= (V, Е).
Выход. Список ребер каждой
двусвязной компоненты графа G.
Метод.
Вначале полагаем Т= и СЧЕТ=1. Помечаем каждый узел в V как "белый", выбираем произвольный узел v0 в V, П[v0] = 0 и вызываем Поиск_дк(v0), чтобы построить глубинное остовное дерево S= (V,Т) и вычислить low[v] для каждого v из V.
Слайд 13
Процедура Поиск_дк(v)
Поиск_дк(v)
{ цвет [v] ← серый; dfnumber[v]
СЧЕТ++;
low[v] dfnumber[v] ;
для w
смежные(v) выполнить
{ если (цвет[w] == белый) то
{ поместить (v, w) в СТЕК; добавить (v, w) к Т; п[w] ← v;
Поиск_дк (w);
если low[w] dfnumber[v] то
{ обнаружена двусвязная компонента:
вытолкнуть из СТЕКа все ребра вплоть до ребра (v, w) ;
}
low[v] ← min ( low[v], low[w]);
}
иначе
если (w ≠ п[v]) то
{ если (dfnumber[w] < dfnumber[v] ) то поместить (v, w) в СТЕК;
low[v] ← min ( low[v], dfnumber[w] )
}
}
цвет[v] ← чёрный;
}
Слайд 14
Пример
1
9
2
3
8
4
7
5
6
V1
V3
V2
V4
V5
V6
V7
V8
V9
low[1]=
low[2]=
low[3]=
low[4]=
low[5]=
low[6]=
low[7]=
low[8]=
low[9]=
1
2
3
4
5
6
7
8
9
4
4
4
2
2
1
(V1, V2)
(V2, V4)
(V4, V6)
(V6, V9)
(V9, V8)
(V8, V6)
(V9, V7)
(V7,
V6)
(V4, V5)
(V5, V2)
(V2, V3)
(V3, V1)
1
Стек
V1
V2
V4
V6
V9
V8
V7









![Двусвязность Процедура Поиск_дк(v)Поиск_дк(v){ цвет [v] ← серый; dfnumber[v] СЧЕТ++; low[v] ](/img/tmb/13/1245602/a4cda29546841788ffd396cc7c00442f-720x.jpg)
![Двусвязность Пример192384756V1V3V2V4V5V6V7V8V9low[1]=low[2]=low[3]=low[4]=low[5]=low[6]=low[7]=low[8]=low[9]=123456789444221(V1, V2)(V2, V4)(V4, V6)(V6, V9)(V9, V8)(V8, V6)(V9, V7)(V7, V6)(V4, V5)(V5, V2)(V2, V3)(V3, V1)1СтекV1V2V4V6V9V8V7](/img/tmb/13/1245602/eea8052ef6859dd584589526a41b34e5-720x.jpg)