- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Системность реальности
Содержание
- 2. Законы и принципы кибернетикинеобходимого разнообразияэмерджентностивнешнего дополненияобратной связивыбора решениядекомпозициииерархии управления и автоматического регулирования (саморегулирования)
- 3. Закон обратной связи Схема управления с обратной связью (простая замкнутая система)
- 4. По своему назначению математические методы
- 5. С помощью факторного анализа
- 6. Теория Фракталов
- 7. Множество Мандельброта — классический образец фрактала
- 8. Что такое ФРАКТАЛ?! Данное понятие не является
- 9. Определение фрактала Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба
- 10. Многообразие искусственных и природных фракталов
- 11. Треугольник Серпинского
- 12. А теперь поговорим об Иллюзиях Восприятия, в частности об иллюзиях движения
- 13. Цветок Если смотреть в центр цветка, то он будет "распускаться"
- 14. Разбегание Зернышки словно разбегаются из центра
- 15. Мерцание У некоторых людей разглядывание этой
- 16. Воронка Возникает эффект затягивания в воронку
- 17. Часы Часики тикают, хотя на самом деле все шестеренки неподвижны
- 18. Вращающиеся лепестки Интересный эффект вращения лепестков
- 19. СТРЕЛКИ Кажется что стрелки, составленные из красных шариков, движутся друг навстречу другу
- 20. Обман зрения Здесь очень хорошо
- 21. АСФАЛЬТ Вертикальные линии строго
- 22. ЛЕДЕНЕЦ Смотрите в центр изображения
- 23. ЛЕПЕСТКИ Лепестки словно бы крутятся
- 24. МЕРЦАНИЕ Здесь все просто -
- 25. ЦВЕТНАЯ СПИРАЛЬ Не отводя взгляд
- 26. ЕЩЕ ЛЕДЕНЦЫ Спирали крутятся, не так ли?
- 27. ПУЛЬСАЦИЯ Видите пульсирующее изображение? Нет, это всего лишь иллюзия
- 28. Еще танцующие шестеренки
- 29. Пропеллеры Ветра нет, а они крутятся
- 30. Тетрис Картинка постоянно "плывет"
- 31. Снежинка Части этой "снежинки" немного движутся
- 32. Леденцы
- 33. Плавающий паром смотрите на точку чуть ниже «парома»б и он начнет плавать туда-сюда
- 34. Исчезновение Если долго смотреть на один
- 35. Исчезающий объект Не отрываясь, смотрите на квадрат, и вы заметите, что белая линия исчезает
- 36. Исчезающий фон
- 37. Зрительные искажения
- 38. Цилиндр C какой стороны начинается цилиндр?
- 39. Спираль из колючек Это окружности!
- 40. Это не спираль, а концентрические окружности
- 41. А вот нет выпуклости!
- 42. Две параллельные красные линии
- 43. Все параллельно
- 44. И, не поверите, здесь то же! )
- 45. Не очень круглое колесо Внутренняя окружность
- 46. КОВЕР Очень интересный пример
- 47. «Надломленный квадрат»
- 48. А НЕ ВСЕ ЛИ РАВНО ?
- 49. СТАРЫЙ ТЕЛЕВИЗОР В РАЗРЕЗЕ Красные линии равны по длине, хотя правая кажется явно длиннее
- 50. ТЕНЬ Буквы в этом слове словно покосились, но нет, все совершенно ровно
- 51. Параллельно!
- 52. Найди оленей в лесу
- 53. Невозможные пространства Эшера многоногий слон
- 54. Не покупайте такие лестницы!
- 55. Невозможные фигуры
- 56. Невозможные пейзажи
- 57. Творения ЭшераМа́уриц Корне́лис Э́шер (нидерл. Maurits Cornelis Escher
- 58. Сюжеты картинМозаики NB! Математически доказано, что регулярное
- 59. Сюжеты картинМногогранники – октаэдры, додекаэдры, пирамидыМногогранники в
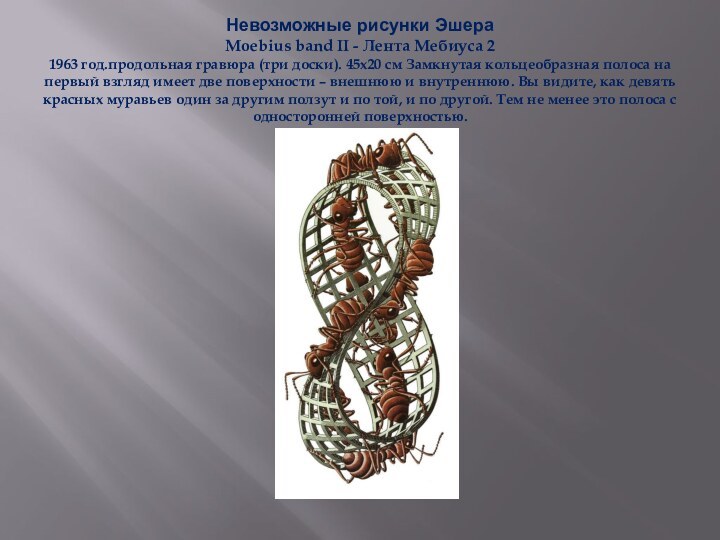
- 60. Невозможные рисунки Эшера Moebius band II -
- 61. Бельведер 1958 год В трехмерном мире невозможно
- 62. Ascending and descending - Вверх и вниз,
- 63. Tower of Babel - Вавилонская башня, 1928.
- 64. Balkony – Балкон, 1945 Трехмерность этих домов – абсолютная иллюзия
- 65. Водопад
- 66. Drawing Hands - Рисующие руки, 1948
- 67. Дракон.1952.
- 68. Древо
- 69. Concentric rinds – Концентрические сферы, 1953 Четыре
- 70. Рептилии Мозаики (Разбиение плоскости)
- 71. День и ночь Мозаики (Разбиение плоскости)
- 72. Encounter – Встреча, 1944
- 73. Меньше и меньше
- 74. Змеи
- 75. Circle Limit III - Предел-круг III, 1959
- 76. Whirlpools – Водовороты, 1957
- 77. Order and chaos - Порядок и Хаос, 1950
- 78. Звезды
- 79. Пространственные спирали
- 80. Скачать презентацию
- 81. Похожие презентации
Законы и принципы кибернетикинеобходимого разнообразияэмерджентностивнешнего дополненияобратной связивыбора решениядекомпозициииерархии управления и автоматического регулирования (саморегулирования)


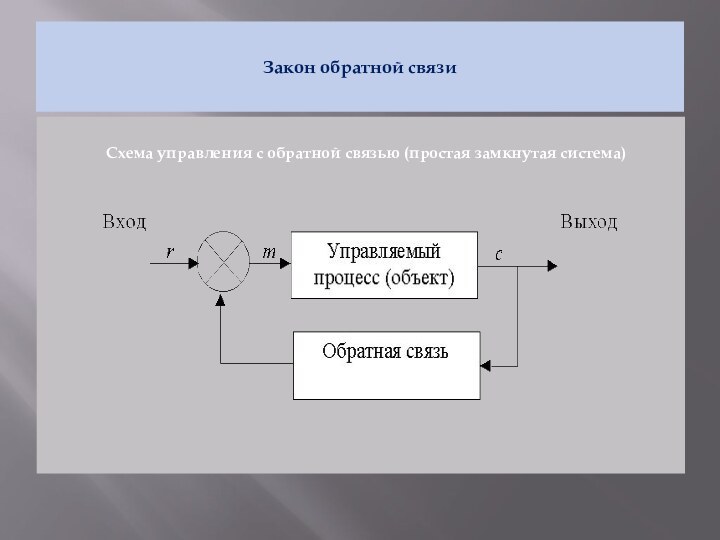












































































Слайд 2
Законы и принципы кибернетики
необходимого разнообразия
эмерджентности
внешнего дополнения
обратной связи
выбора решения
декомпозиции
иерархии
управления и автоматического регулирования (саморегулирования)
Слайд 4
По своему назначению математические методы можно поделить:
Методы предсказания:
множественный регрессионный анализ и дискриминантный анализ.
Множественный регрессионный анализ предсказывает
значение метрической «зависимой» переменной по множеству известных значений «независимых» переменных, измеренных у множества объектов (испытуемых). Дискриминантный анализ предсказывает принадлежность объектов (испытуемых) к одному из известных классов (номинативной шкале) по измеренным метрическим (дискриминантным) переменным.
Методы классификации: варианты кластерного анализа и дискриминантый анализ.
Кластерный анализ по измеренным характеристикам у множества объектов (испытуемых) либо по данным об их попарном сходстве (различии) разбивает множество объектов на группы, в каждом из которых содержатся объекты более похожие друг на друга, чем на объекты других групп.
Дискриминантый анализ позволяет классифицировать объекты по известным классам, исходя из измеренных у них признаков, пользуясь решающими правилами, выработанными предварительно на выборке идентичных объектов, у которых были измерены те же признаки.
Структурные методы: факторный анализ и многомерное шкалирование.
Факторный анализ направлен на выявление структуры переменных как совокупности факторов, каждый из которых – это скрытая, обобщающая причина взаимосвязи группы переменных.
Многомерное шкалирование выявляет шкалы как критерии, по которым поляризуются объекты при их субъективном попарном сравнении.
NB! Чаще всего, факторный анализ используется для построения моделей таких мета-психологических категорий, как: личность и интеллект
Слайд 5 С помощью факторного анализа были созданы модели личности,
интеллекта,
например
Модель интеллекта Дж. Гилфорда
Слайд 7 Множество Мандельброта — классический образец фрактала (см.предыдущий слайд), так
же как и подвид цветной капусты (Brassica cauliflora)
Слайд 8
Что такое ФРАКТАЛ?!
Данное понятие не является математическим
термином и не
имеет общепринятого строгого математического определения.
Оно может употребляться,
когда рассматриваемая фигураобладает какими-либо из перечисленных ниже свойств:
Обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.
Является самоподобной или приближённо самоподобной.
Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
Может быть построена при помощи рекурсивной процедуры
Слайд 9
Определение фрактала
Фрактал — это бесконечно самоподобная геометрическая фигура,
каждый фрагмент которой повторяется при уменьшении масштаба
Слайд 15 Мерцание У некоторых людей разглядывание этой картинки вызывает неприятные
ощущения, возможно из-за эффекта слишком частого мерцания
Слайд 19 СТРЕЛКИ Кажется что стрелки, составленные из красных шариков,
движутся друг навстречу другу
Слайд 20 Обман зрения Здесь очень хорошо видно, насколько обманчиво
наше зрение. Круги полностью неподвижны. Не верите? Сфокусируйтесь на
одном из них, и он перестанет вращатьсяСлайд 21 АСФАЛЬТ Вертикальные линии строго параллельны. Кроме того, по
рисунку как будто бежит волна
Слайд 22 ЛЕДЕНЕЦ Смотрите в центр изображения и подвигайте головой вперед-назад.
Разноцветные окружности будут двигаться, одна по часовой стрелке, а
другая противСлайд 24 МЕРЦАНИЕ Здесь все просто - картинка мерцает и
немного переливается, особенно если смотреть в центр
Слайд 25 ЦВЕТНАЯ СПИРАЛЬ Не отводя взгляд от центра рисунка
приблизьтесь к экрану, а затем отдалитесь, и вы увидите,
что цветная спираль движетсяСлайд 34 Исчезновение Если долго смотреть на один шарик, не отрывая
взгляд, то один или даже несколько шариков исчезнут. Но
видят такой эффект не всеСлайд 35 Исчезающий объект Не отрываясь, смотрите на квадрат, и вы
заметите, что белая линия исчезает
Слайд 45 Не очень круглое колесо Внутренняя окружность на фоне большого
колеса кажется искаженной, хотя она абсолютно ровная
Слайд 46 КОВЕР Очень интересный пример ровных и параллельных линий.
Это как раз тот случай, когда не поверишь, пока
не приложишь к рисунку линейку
Слайд 57
Творения Эшера
Ма́уриц Корне́лис Э́шер (нидерл. Maurits Cornelis Escher (
17 июня 1898 – 27 марта 1972) — нидерландский
художник- график. Известен прежде всего своими концептуальными литографиями, гравюрами на дереве и металле, в которых он мастерски исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трехмерных объектов.«Хотя я абсолютно несведущ в точных науках, мне иногда кажется, что я ближе к математикам, чем к моим коллегам-художникам»
Слайд 58
Сюжеты картин
Мозаики NB! Математически доказано, что регулярное замощение
плоскости возможно только тремя правильными многоугольниками: треугольником, квадратом и
шестиугольником. Эшер интересовался как регулярными мозаиками, так и нерегулярными. Кроме того, что художник использовал нерегулярные мозаики (образующие неповторяющиеся узоры), он много работал с метаморфозами, изменяя многоугольники под зооморфные формы, заполняющие поверхность. Интерес к мозаикам проявился в 1936 во время путешествия в Испании под влиянием геометрических орнаментов Альгамбры.
Слайд 59
Сюжеты картин
Многогранники – октаэдры, додекаэдры, пирамиды
Многогранники в работах
Эшера играют роль как основной фигуры, так и вспомогательных
элементов. В работах «Порядок и хаос» и «Звёзды» художник использует негеометрические формы для усиления впечатления от правильности центральных фигур, в конструкции из трех правильных полых октаэдров живут два хамелеона.Многоугольники, как и сферы, используются в работах Эшера для создания перспективы. Последней литографией в серии многоугольников была «Гравитация». На ней изображён додекаэдр, образованный двенадцатью плоскими пятиконечными звёздами. На каждой из площадок живёт длинношеее четырёхногое бесхвостое фантастическое животное; его туловище находится в пирамиде, в отверстия которой оно высовывает конечности, верхушка пирамиды является одной из стен жилища соседнего чудовища. Пирамиды одновременно выступают и как стены, и как полы: литография служит переходом к группе относительности.





























