- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Электромагнитные волны.
Содержание
- 2. Электромагнитная теорияВ XIX веке развитие электромагнитной теории
- 3. Электромагнитные волныСуществование электромагнитных волн теоретически предсказал великий английский физик Джеймс Клерк Максвелл в 1864 году.
- 4. Уравнения Максвелла.Максвелл проанализировал все известные к тому
- 5. 1. Теорема Гаусса для электрического поля.
- 6. 2. Теорема Гаусса для магнитного поля.Поток вектора
- 7. 3. Закон электромагнитной индукции.Как известно, вследствие явления
- 8. 3. Закон электромагнитной индукции.Таким образом, ЭДС индукции
- 9. 4. Теорема о циркуляции вектора магнитной
- 10. Источники магнитного поляМаксвелл предположил, что источником магнитного
- 11. Ток смещенияНапример, через конденсатор постоянный ток не
- 12. Здесь q изменяющийся заряд конденсатора, который
- 13. Четвертое уравнение Максвелла,
- 14. Физический смысл уравнений Максвелла.1 уравнение Максвелла является
- 15. Физический смысл уравнений Максвелла.2 уравнение Максвелла –
- 16. Физический смысл уравнений Максвелла.3 уравнение Максвелла. Всякое
- 17. Физический смысл уравнений Максвелла.4 уравнение Максвелла. Изменяющееся
- 18. Следствия из уравнений Максвелла.1. Существует особая форма
- 19. Следствия из уравнений Максвелла.2. Существуют электромагнитные волны,
- 20. Следствия из уравнений Максвелла.3. Электромагнитные волны –
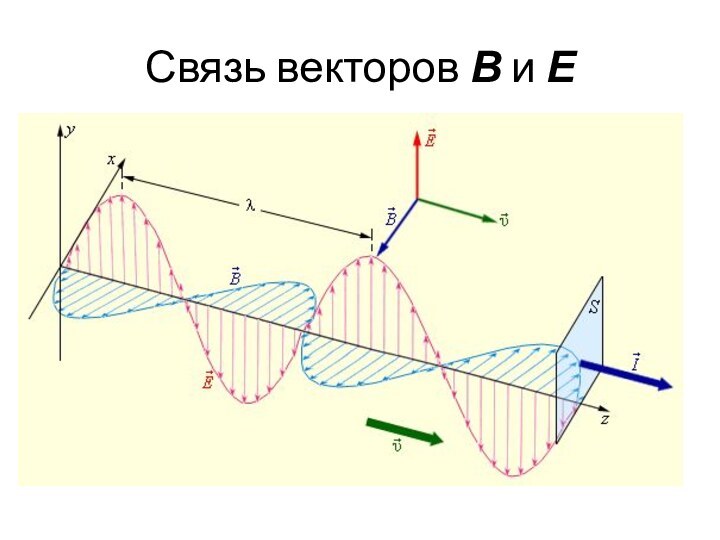
- 21. Связь векторов В и Е
- 22. Т.к. электромагнитное поле в волне не связано
- 23. Следствия из уравнений Максвелла.4. Электромагнитные волны распространяются
- 24. Следствия из уравнений Максвелла.Скорость распространения электромагнитных волн
- 25. Следствия из уравнений Максвелла.Приравнивая эти выражения, получим
- 26. Следствия из уравнений Максвелла.5. В электромагнитной волне
- 27. Следствия из уравнений Максвелла.6. Электромагнитные волны переносят
- 28. Плотностью потока энергии или интенсивностью I называется
- 29. Поток энергии в электромагнитной волне можно задавать
- 30. Следствия из уравнений Максвелла.7. Электромагнитные волны имеют
- 31. Следствия из уравнений Максвелла.8. Электромагнитные волны оказывают
- 32. Эта сила и создает результирующее давление. Обычно
- 33. §2. Генерация электромагнитных волн.
- 34. Первое экспериментальное подтверждение электромагнитной теории Максвелла было
- 35. Ему удалось измерить на опыте длину волны
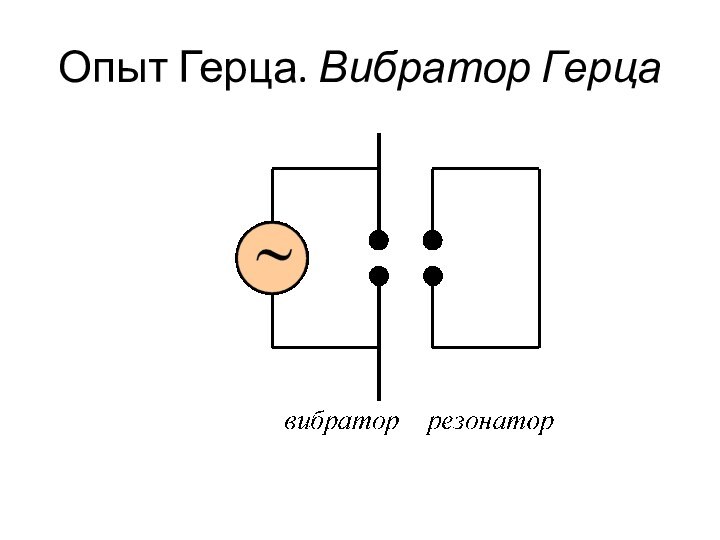
- 36. Опыт Герца. Вибратор Герца
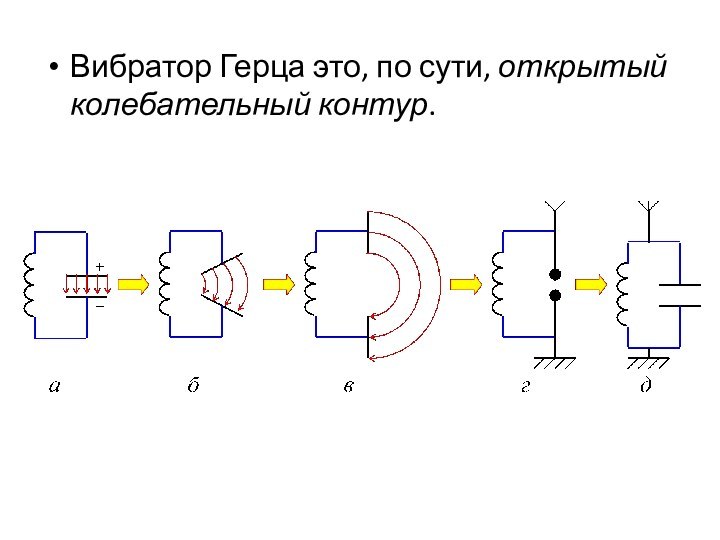
- 37. Вибратор Герца это, по сути, открытый колебательный контур.
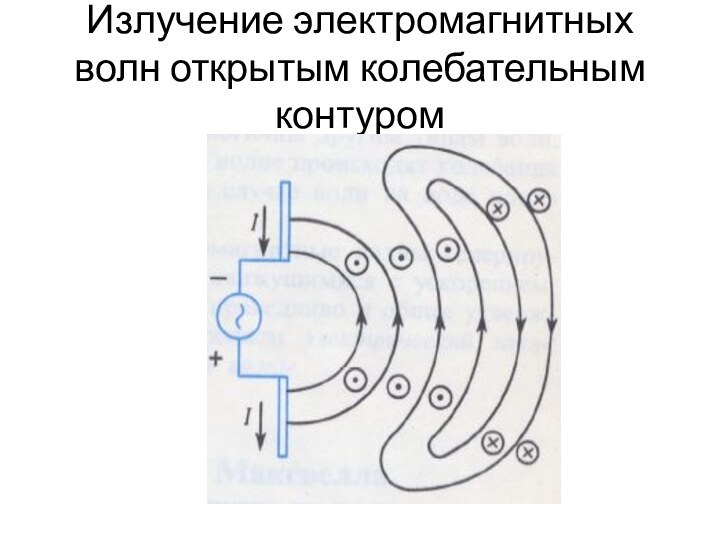
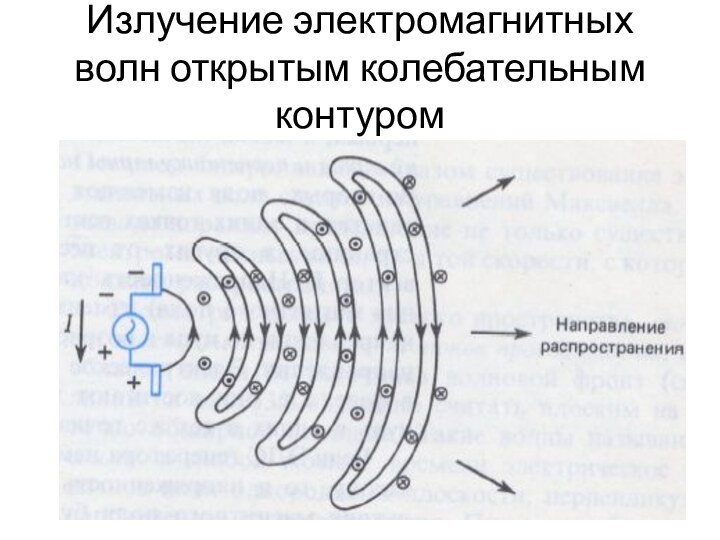
- 38. Излучение электромагнитных волн открытым колебательным контуром
- 39. Излучение электромагнитных волн открытым колебательным контуром
- 40. Излучение электромагнитных волн открытым колебательным контуром
- 41. Выводы1. Электромагнитные волны – поперечные.2. Электромагнитные волны
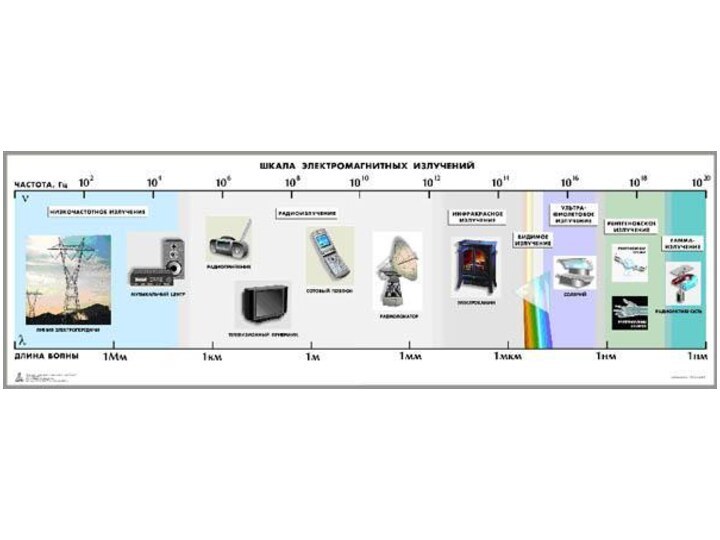
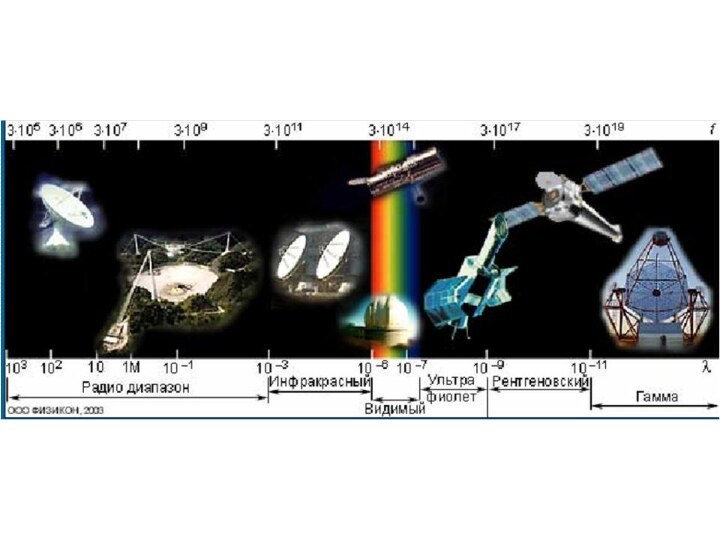
- 42. §3. Шкала электромагнитных волн.
- 43. радиоволны1. Радиоволнами называются электромагнитные волны, длина волны
- 44. Оптическое излучение2. Оптическим излучением, или светом, называются
- 46. Рентгеновское излучение3. Рентгеновским излучением называется электромагнитное излучение,
- 48. Гамма-излучениеГамма-излучением (или гамма-лучами) называется электромагнитное излучение с
- 49. Скачать презентацию
- 50. Похожие презентации
Электромагнитная теорияВ XIX веке развитие электромагнитной теории привело к предсказанию, а в последствии и экспериментальному подтверждению способности электромагнитных полей распространяться в пространстве. Это достижение открыло возможность создания новых средств связи: вначале беспроволочного телеграфа, затем радио и









































Слайд 3
Электромагнитные волны
Существование электромагнитных волн теоретически предсказал великий английский
физик Джеймс Клерк Максвелл в 1864 году.
Слайд 4
Уравнения Максвелла.
Максвелл проанализировал все известные к тому времени
законы электродинамики и показал, что все электрические и магнитные
явления можно описать всего четырьмя уравнениями. Эти уравнения также фундаментальны, как и законы Ньютона. На их основе было предсказано существование электромагнитных волн.
Слайд 5
1. Теорема Гаусса для электрического поля.
Поток вектора напряженности
электрического поля через площадку площади S равен
,где n – нормаль к площадке.
Обозначим поток напряженности электрического поля через любую замкнутую поверхность S
Тогда теорема Гаусса для электрического поля имеет вид:
(первое уравнение Максвелла).
Слайд 6
2. Теорема Гаусса для магнитного поля.
Поток вектора магнитной
индукции B через произвольную замкнутую поверхность обозначим аналогично потоку
вектора напряженности EТогда теорема Гаусса для магнитного поля представляется в виде
второе уравнение Максвелла
.
Слайд 7
3. Закон электромагнитной индукции.
Как известно, вследствие явления электромагнитной
индукции изменение магнитного потока порождает вихревое электрическое поле. ЭДС
индукции Eи, по определению, связана с работой сторонних сил по переносу электрического заряда q по произвольному замкнутому контуру L.
Слайд 8
3. Закон электромагнитной индукции.
Таким образом, ЭДС индукции равна
циркуляции CE вектора напряженность вихревого электрического поля E. В
результате закон электромагнитной индукции можно записать в виде:(третье уравнение Максвелла).
Слайд 9
4. Теорема о циркуляции вектора магнитной индукции.
Циркуляция вектора
B в вакууме магнитного поля постоянных токов по любому
замкнутому контуру L прямо пропорциональна алгебраической сумме токов, охватываемых этим контуром.Максвелл обобщил теорему о циркуляции вектора магнитной индукции, добавив в правую часть уравнения еще одно слагаемое 0Iсмещ., где Iсмещ. так называемый, ток смещения, связанный с изменением электрического поля.
Слайд 10
Источники магнитного поля
Максвелл предположил, что источником магнитного поля
может служить не только электрический ток, но и изменяющееся
во времени электрическое поле (по аналогии с тем, что изменяющееся магнитное поле порождает электрическое поле).
Слайд 11
Ток смещения
Например, через конденсатор постоянный ток не течет,
однако может течь переменный ток разряда, связанный с изменением
электрического поля внутри конденсатора, т.е. “ток смещения”, который равенСлайд 12 Здесь q изменяющийся заряд конденсатора, который выражается
через напряженность E электрического поля внутри конденсатора.
где S –
площадь пластин конденсатора.Т.к. вне конденсатора напряженность электрического поля E = 0, то поток вектора напряженности через любую замкнутую поверхность, внутри которой лежит одно из пластин конденсатора . Тогда ток смещения равен
Слайд 14
Физический смысл уравнений Максвелла.
1 уравнение Максвелла является обобщением
закона Кулона. Оно связывает электрическое поле с его источниками
– электрическими зарядами. Это основное уравнение электростатики.
Слайд 15
Физический смысл уравнений Максвелла.
2 уравнение Максвелла – есть
математическое выражение факта отсутствия изолированных магнитных зарядов. Это основное
уравнение магнитостатики.
Слайд 16
Физический смысл уравнений Максвелла.
3 уравнение Максвелла. Всякое изменение
магнитного поля порождает в окружающем пространстве вихревое электрическое поле,
силовые линии которого замкнуты.
Слайд 17
Физический смысл уравнений Максвелла.
4 уравнение Максвелла. Изменяющееся во
времени электрическое поле порождает в окружающем пространстве магнитное поле.
Уравнения
Максвелла описывают всю совокупность электрических и магнитных явлений, а также оптические явления.
Слайд 18
Следствия из уравнений Максвелла.
1. Существует особая форма материи
– электромагнитное поле, характеризующееся двумя векторами: E и B.
В частном случае неизменных (стационарных) полей имеется либо только электрическое поле (B = 0, E 0), либо только магнитное поле (E = 0, B 0).
Слайд 19
Следствия из уравнений Максвелла.
2. Существуют электромагнитные волны, то
есть распространяющееся в пространстве и во времени электромагнитное поле.
Это следует из третьего и четвертого уравнений Максвелла, т.к. переменное электрическое поле порождает переменное магнитное поле, которое в свою очередь порождает переменное электрическое поле, и т.д., т.е. происходит периодический или волнообразный процесс.В электромагнитной волне происходят колебания полей, а не вещества, как в случае механических волн.
Слайд 20
Следствия из уравнений Максвелла.
3. Электромагнитные волны – поперечные
волны, т.е. векторы E и B в электромагнитной волне
перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны При этом векторы V, E и B образуют правую тройку.Уравнение электромагнитной волны, изображенной на рис. имеет вид:
Слайд 22 Т.к. электромагнитное поле в волне не связано с
источником излучения, то векторы E и B могут изменяться
в пространстве, как по величине, так и по направлению, при этом векторы E и B остаются взаимно перпендикулярными.Если каждый из векторов E и B остается все время в одной плоскости, то такая волна называется линейно поляризованной (плоско поляризованной).
Плоскость, проходящая через векторы V и E называется плоскостью поляризации.
Возможны также и другие виды поляризации, например, циркулярная поляризация, когда вектор E вращается по кругу.
Слайд 23
Следствия из уравнений Максвелла.
4. Электромагнитные волны распространяются в
веществе с конечной скоростью.
Скорость распространения электромагнитных волн в вакууме
равнаПодставляя в эту формулу значения электрической и магнитной постоянных, получим
Слайд 24
Следствия из уравнений Максвелла.
Скорость распространения электромагнитных волн в
вакууме равна скорости света c. Отсюда Максвелл сделал вывод,
что свет – это электромагнитная волна.Скорость электромагнитной волны в среде зависит от диэлектрической и магнитной проницаемости среды
Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.
Слайд 25
Следствия из уравнений Максвелла.
Приравнивая эти выражения, получим связь
между напряженностью электрического поля E и индукцией B магнитного
поля в электромагнитной волне.При распространении электромагнитной волны в среде эта связь имеет вид:
Слайд 26
Следствия из уравнений Максвелла.
5. В электромагнитной волне происходят
взаимные превращения электрического и магнитного полей. Эти процессы идут
одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: .В вакууме объемные плотности электрической и магнитной энергии вычисляются по формулам:
и .
Слайд 27
Следствия из уравнений Максвелла.
6. Электромагнитные волны переносят энергию.
При распространении волн возникает поток электромагнитной энергии. Если выделить
площадку S (см. рис. 4.1.1), ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔWэм, равнаяСлайд 28 Плотностью потока энергии или интенсивностью I называется электромагнитная
энергия, переносимая волной за единицу времени через поверхность единичной
площади:Воспользуемся формулами для плотности энергии и скорости электромагнитной волны и получим следующие выражения для плотности потока энергии:
Слайд 29 Поток энергии в электромагнитной волне можно задавать с
помощью вектора I, направление которого совпадает с направлением распространения
волны, а модуль равен плотности потока энергии, вычисляемой по формуле. Этот вектор называют вектором Умова-Пойнтинга (1885 г.).Плотность потока энергии в СИ измеряется в ваттах на квадратный метр (Вт/м2).
Слайд 30
Следствия из уравнений Максвелла.
7. Электромагнитные волны имеют такие
же свойства, как и механические волны. Поэтому для них
характерны такие явления, как отражение, преломление, интерференция и дифракция.
Слайд 31
Следствия из уравнений Максвелла.
8. Электромагнитные волны оказывают давление
на поглощающее или отражающее тело. Давление электромагнитного излучения объясняется
на основе теории Максвелла тем, что под действием электрического поля волны в веществе возникают слабые токи, то есть упорядоченное движение заряженных частиц. На эти токи действует сила Ампера со стороны магнитного поля волны, направленная в толщу вещества.Слайд 32 Эта сила и создает результирующее давление. Обычно давление
электромагнитного излучения ничтожно мало. Так, например, давление солнечного излучения,
приходящего на Землю, на абсолютно поглощающую поверхность составляет примерно 5 мкПа. Первые эксперименты по определению давления излучения на отражающие и поглощающие тела, подтвердившие вывод теории Максвелла, были выполнены П. Н. Лебедевым (1900 г.). Опыты Лебедева имели огромное значение для утверждения электромагнитной теории Максвелла.Существование давления электромагнитных волн позволяет сделать вывод о том, что электромагнитному полю присущ механический импульс.
Слайд 34 Первое экспериментальное подтверждение электромагнитной теории Максвелла было получено
спустя 10 лет после смерти Максвелла в 1887 году.
Генрих Герц поставил ряд опытов, из которых было доказано существование электромагнитных волн и изучены их свойства, такие как прямолинейность распространения, поглощение и преломление в разных средах, отражение от металлических поверхностей и т. п.Слайд 35 Ему удалось измерить на опыте длину волны и
скорость распространения электромагнитных волн, которая оказалась равной скорости света.
Опыты Герца сыграли решающую роль для доказательства и признания электромагнитной теории Максвелла. Через семь лет после этих опытов электромагнитные волны нашли применение в беспроволочной связи (А. С. Попов, 1895 г.).
Слайд 41
Выводы
1. Электромагнитные волны – поперечные.
2. Электромагнитные волны генерируются
колеблющимися, т.е. движущимися с ускорением электрическими зарядами. Справедливо и
более общее утверждение: движущийся с ускорением электрический заряд излучает электромагнитные волны.
Слайд 43
радиоволны
1. Радиоволнами называются электромагнитные волны, длина волны которых
в вакууме > 510-5 м (соответственно частота
< 61012 Гц).Здесь выделяют область длинных волн: > 1 км ( < 3105 Гц),
средних волн: = 100 м 1 км ( = 3105 3106 Гц),
коротких волн: = 10 м 100 м ( = 3106 3107 Гц),
УКВ ультракоротких волн: < 10 м ( > 3107 Гц).
Слайд 44
Оптическое излучение
2. Оптическим излучением, или светом, называются электромагнитные
волны, длины которых в вакууме лежат в интервале
= 10 нм – 1 мм (1 нм = 10-9 м).Оптическое излучение разделяется на
а) инфракрасное излучение – электромагнитное излучение, испускаемое нагретыми телами, длины волн которого в вакууме лежат в пределах = 770 нм – 1 мм;
б) видимое излучение (видимый свет) – электромагнитное излучение с длинами волн в вакууме = 380 нм – 770 нм , которое способно непосредственно вызывать зрительное ощущение в человеческом глазе;
в) ультрафиолетовое излучение– электромагнитное излучение с длинами волн в вакууме = 10 нм – 380 нм. Ультрафиолетовое излучение получается с помощью тлеющего разряда, обычно в парах ртути.