- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Электронный парамагнитный резонанс
Содержание
- 2. Явление ЭПРСуть явления электронного парамагнитного резонанса заключается
- 3. Явление открыто в 1944 г. в Казанском
- 4. В СССР в 1958 году впервые Л.А.
- 5. Метод , основанный на явлении ЭПР, является
- 6. Парамагнитные частицы имеющим важное биологическое значение и
- 7. Свободные радикалы— частицы (как правило,неустойчивые), содержащие один
- 8. Радикал может образоваться в результате потери одного
- 9. OOOO+ е- + е- +2H+OOHH+H+OOH+ е- +
- 10. Электрон в атоме e-PllPSz
- 11. Квантовые числаСостояние каждого электрона в атоме обычно
- 12. Орбитальные механический и магнитный моменты электронаОрбитальный механический
- 13. СпинСпин — собственный момент импульса элементарных частиц.
- 14. S – спиновый магнитный момент, PS– спиновый
- 15. Полные механический и магнитный моменты электронаПолный магнитный
- 16. g-фактор (магнитомеханическое отношение)g-фактор используют для удобства
- 17. Орбитальные и спиновые моменты атомов с несколькими
- 18. Явление ЭПРФизическая картина явленияЯвление магнитного резонанса можно объяснить в рамках классической и квантовой физики.
- 19. Квантовомеханическая интерпретация ЭПРДля выяснения физической картины явления
- 20. Эффект ЗееманаH0EHРасщепление энергетических уровней электронов в магнитном
- 21. Явление ЭПРПоглощение электромагнитного излучениянеспаренными электронами, находящимися в
- 22. Принцип метода ЭПР В основе метода ЭПР
- 23. Согласно распределению Больцмана у парамагнетиков в состоянии
- 24. Суть явления магнитной релаксации:парамагнитные частицы могут обмениваться
- 25. Классическая интерпретация ЭПР M совершает круговые вращения по
- 26. E = - (M Н)
- 27. Условием резонансного поглощения энергии электромагнитного излучения является
- 28. Устройство радиоспектрометра ЭПРЭкспериментально подобрать условия парамагнитного резонанса
- 29. Регистрация поглощения электромагнитного излученияв постоянном магнитном поле
- 30. Схема простейшей установки для регистрации ЭПР а
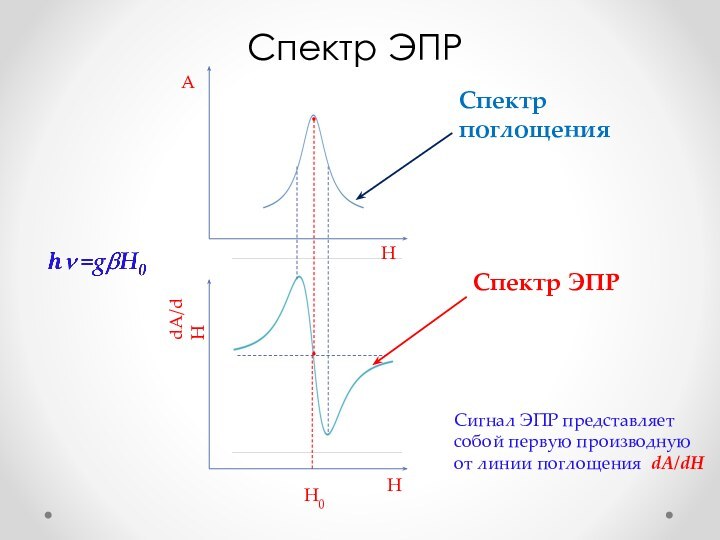
- 31. Спектр ЭПРСпектр поглощения Спектр ЭПРСигнал ЭПР представляет собой первую производную от линии поглощения dA/dH AdA/dHHHH0
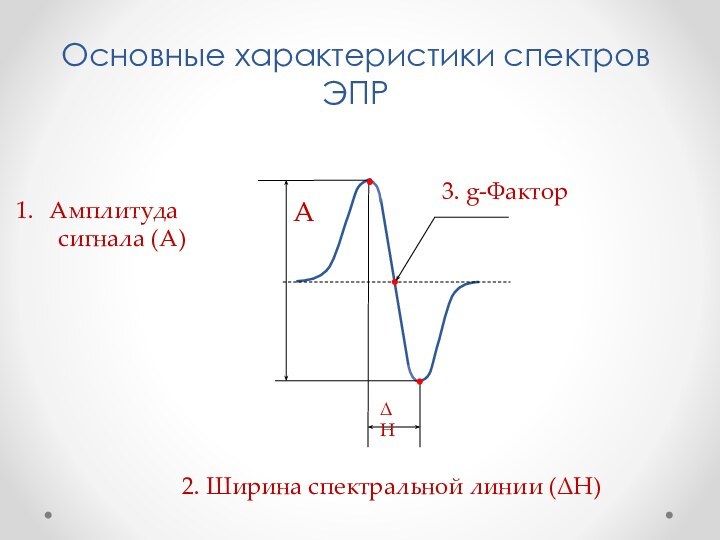
- 32. Основные характеристики спектров ЭПРАмплитуда сигнала (A) 2. Ширина спектральной линии (H)3. g-ФакторHA
- 33. где Cx. и C0 - концентрации измеряемого
- 34. (концентрация парамагнитных центров пропорциональна первому интегралу под
- 35. Форма линииЕсли можно пренебречь взаимодействием между парамагнитными
- 36. 2. Ширина спектральной линииШирина спектральной линии H
- 37. Время релаксацииВремена релаксации Т1 и Т2 зависят
- 38. Ширина спектральной линии и время релаксацииШирина одиночной
- 39. Механизмы уширения сигнала ЭПРВзаимодействие магнитных моментов двух
- 40. 3. g-Фактор g-фактор - параметр, отражающий вклад
- 41. g-ФакторПричины значительного отклонения g-фактора от чисто спинового
- 42. Сверхтонкое взаимодействиеАтомные ядра, у которых нечетно хотя
- 43. Спин и магнитный момент ядраЯдро атома будет
- 44. Протон имеет магнитный момент p, который ориентирован
- 45. Сверхтонкая структура спектров ЭПРНеспаренный электрон в радикале
- 46. Сверхтонкая структура спектров ЭПРHzxySz=+1/2Sz=-1/2Sz=1=gH+1Jz=000+1-1-1H0=h/gСхема энергетических уровней, иллюстрирующая
- 47. Тонкая структура спектров ЭПРЕсли спиновый и орбитальный
- 48. Исследование формы спектра ЭПР в зависимости от
- 49. Перечисленные выше характеристики спектров ЭПР — g-фактор,
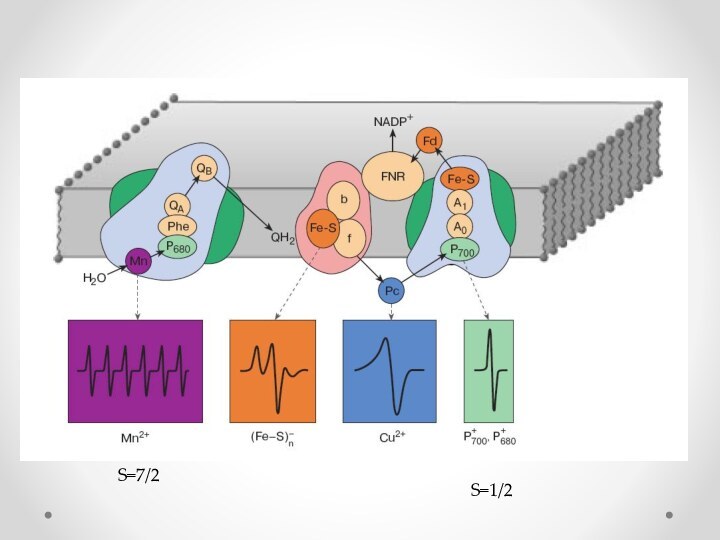
- 50. S=7/2S=1/2
- 51. Естественные сигналы ЭПР, наблюдаемые в биологических системах
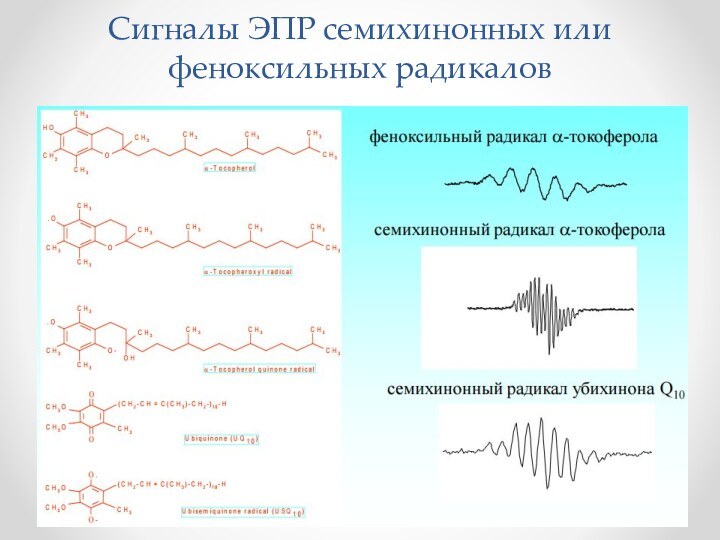
- 52. Сигналы ЭПР семихинонных или феноксильных радикалов
- 53. Метод спиновых зондов
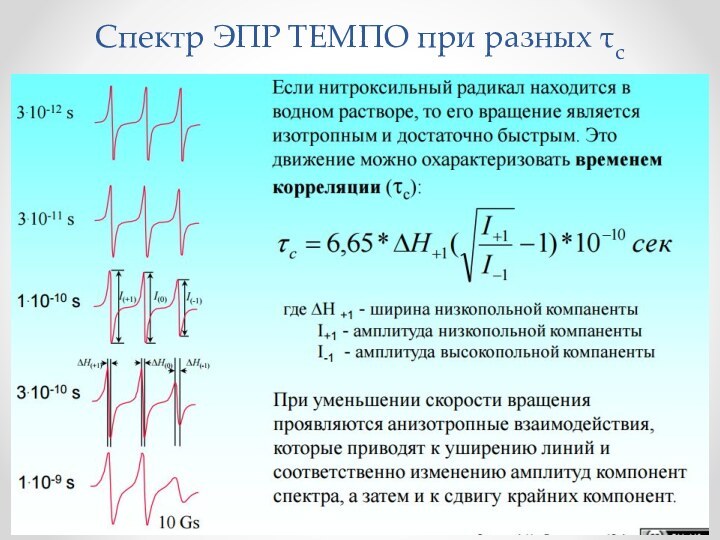
- 54. Cпектр ЭПР ТЕМПО при разных c
- 55. Время корреляции нитроксильного радикала непосредственно связано с микровязкостью среды
- 56. Параметр гидрофобности f
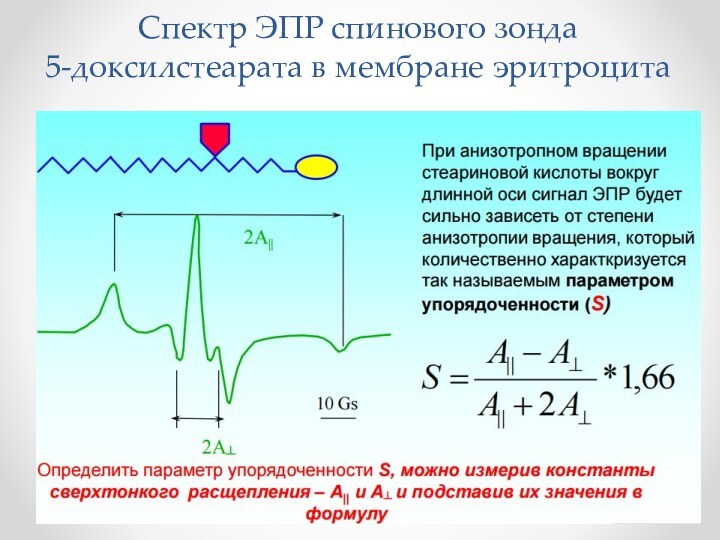
- 57. Спектр ЭПР спинового зонда 5-доксилстеарата в мембране эритроцита
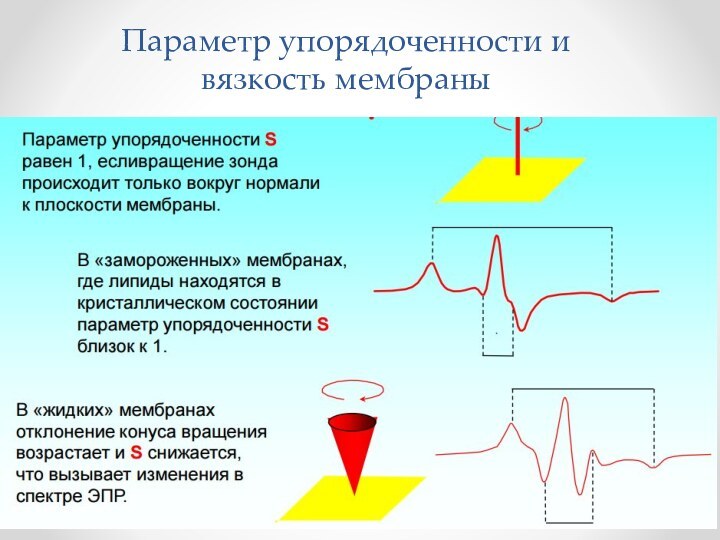
- 58. Параметр упорядоченности и вязкость мембраны
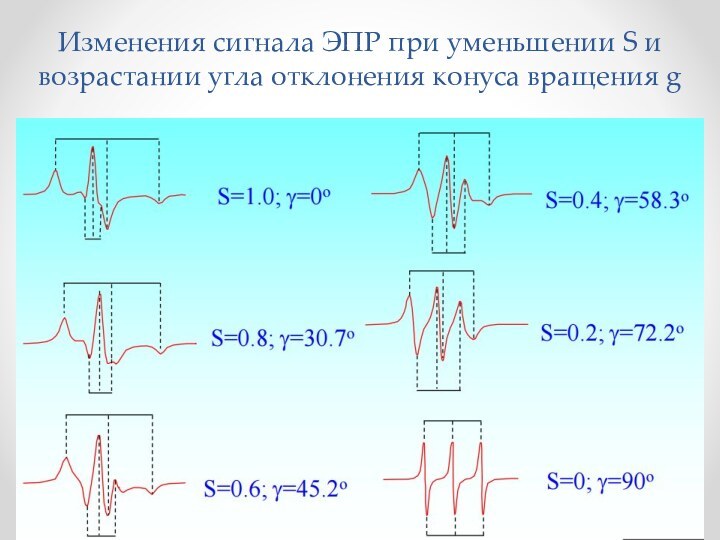
- 59. Изменения сигнала ЭПР при уменьшении S и возрастании угла отклонения конуса вращения g
- 60. Изменения сигнала ЭПР при удалении нитроксильного радикала от полярной карбоксильной группы жирной кислоты
- 61. Спектр ЭПР рН чувствительного зонда (pK=4,7) при разных рН
- 62. Спектр ЭПР химотрипсина с присоединенной спиновой меткой
- 63. Спектры ЭПР спиновой метки при взаимодействии с SH-группами белка
- 64. Литература1. Дж. Вертц и Дж. Болтон Теория
- 65. Вопросы к зачету1. Магнитные свойства веществ. Орбитальный
- 66. Энергия ядра в магнитном поле
- 67. Скачать презентацию
- 68. Похожие презентации










































Слайд 3 Явление открыто в 1944 г. в Казанском Университете
Е. К. ЗАВОЙСКИМ при исследовании поглощения электромагнитной энергии парамагнитными
солями металлов.Монокристалл CuCl2, помещенный в постоянное магнитное поле 40 гаусс (В=4 мТл) начинает поглощать микроволновое излучение с частотой около =133 МГц.
Слайд 4
В СССР в 1958 году впервые
Л.А. Блюменфельд
и А.Э. Калмансон
применили метод ЭПР в биологических исследованиях
при
изучении свободных радикалов, полученных под действием ионизирующего излучения на белки.Слайд 5 Метод , основанный на явлении ЭПР, является основным
методом
для изучения парамагнитных частиц присутствующих в биологических системах.
Слайд 6 Парамагнитные частицы имеющим важное биологическое значение и состояния
исследуемые методом ЭПР
свободные радикалы
металлы переменной валентности или их
комплексы (Fe, Cu, Co, Ni, Mn)а также
триплетные состояния, возникающие, например, в ходе фотобиологических процессов
Слайд 7
Свободные радикалы— частицы (как правило,
неустойчивые), содержащие один или
несколько неспаренных электронов на внешней электронной оболочке.
молекулы O2 (в
основном, триплетном состоянии), NO, NO2, ClO2Слайд 8 Радикал может образоваться в результате потери одного электрона
нерадикальной молекулой:
D→ e¯+ D+
• или при получении одного
электрона нерадикальной молекулой: A + e¯→ A¯
• органические радикалы образуются, например , при окислении (при отрыве атома водорода) :
С
O
H
H
H
H
С
O
H
H
H
- е- - H+
метанол
радикал метанола
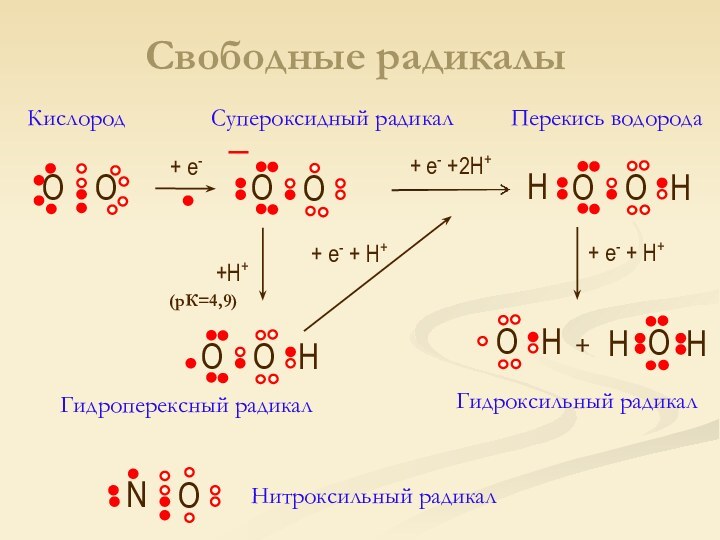
Слайд 9
O
O
O
O
+ е-
+ е- +2H+
O
O
H
H
+H+
O
O
H
+ е- + H+
O
H
Перекись
водорода
Гидроксильный радикал
Супероксидный радикал
Кислород
Гидроперексный радикал
N
O
Нитроксильный радикал
Свободные радикалы
(рК=4,9)
+ е- + H+
O
H
H
+
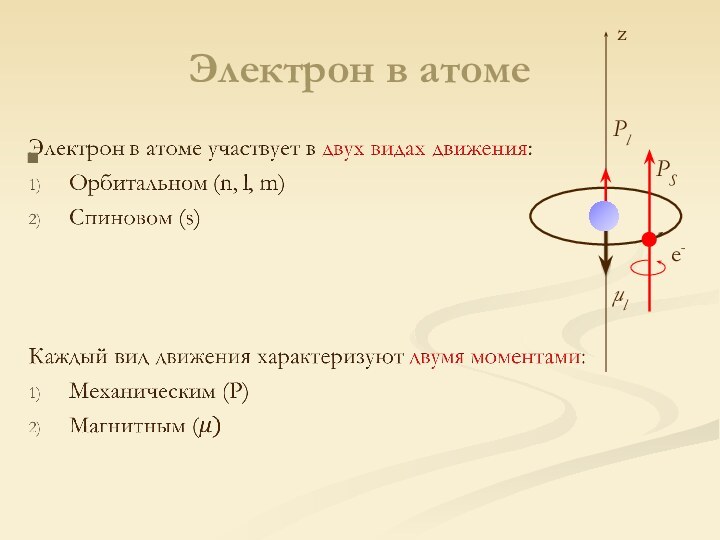
Слайд 11
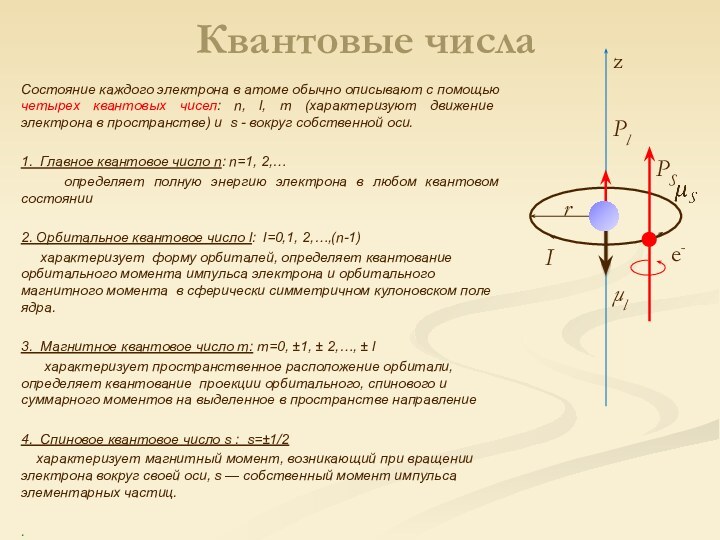
Квантовые числа
Состояние каждого электрона в атоме обычно описывают
с помощью четырех квантовых чисел: n, l, m (характеризуют
движение электрона в пространстве) и s - вокруг собственной оси.1. Главное квантовое число n: n=1, 2,…
определяет полную энергию электрона в любом квантовом состоянии
2. Орбитальное квантовое число l: l=0,1, 2,…,(n-1)
характеризует форму орбиталей, определяет квантование орбитального момента импульса электрона и орбитального магнитного момента в сферически симметричном кулоновском поле ядра.
3. Магнитное квантовое число m: m=0, 1, 2,…, l
характеризует пространственное расположение орбитали, определяет квантование проекции орбитального, спинового и суммарного моментов на выделенное в пространстве направление
4. Спиновое квантовое число s : s=1/2
характеризует магнитный момент, возникающий при вращении электрона вокруг своей оси, s — собственный момент импульса элементарных частиц.
.
e-
I
r
Pl
l
z
PS
Слайд 12
Орбитальные механический и магнитный моменты электрона
Орбитальный механический момент
классический
Орбитальный магнитный момент
m- масса, v - скорость,
e – заряд, r – радиус орбиты электрона, I - сила тока в контуре, а S - площадь контура, ħ =h/2 =1,055 *10-34Дж*с – постоянная Дирака – единица измерения механического момента импульса , h=6,626 *10-34Дж*с – постоянная Планка, =9,27*10-21Дж/м*Тл - единица измерения магнитного момента электронов и атомов- магнетон Бора
из квантовой физики
Слайд 13
Спин
Спин — собственный момент импульса элементарных частиц.
Спин
измеряется в единицах ħ(приведённая постоянная Планка) и равен ħJ,
где J — характерное для каждого сорта частиц целое (в т.ч. нулевое) или полуцелое положительное число — спиновое квантовое число, или спин.Все элементарные частицы по величине спина делятся на два класса:
бозоны — частицы с целым спином (например, фотон) - ħ.
фермионы — частицы с полуцелым спином (например, электрон, протон, нейтрон, нейтрино) – ħ/2;
Спин J ядра наряду с его массой M является механической характеристикой системы нуклонов. Спин ядра J складывается из спиновых s1 - sA и орбитальных l1 - lA моментов отдельных нуклонов: нуклоны обладают собственным механическим моментом, или спином, равным ħ/2, орбитальные моменты принимают только целочисленные значения ħ
Для спинов атомных ядер экспериментально установлены следующие закономерности:
если A – чётное, то J = n (n = 0, 1, 2, 3,...), т.е. спин ядра имеет целочисленное значение;
если A – нечётное, то J = n + 1/2, т.е. спин ядра имеет полуцелое значение;
чётно-чётные ядра в основном состоянии имеют значение спина J= 0, что указывает на взаимную компенсацию моментов нуклонов в основном состоянии ядра – особое свойство межнуклонного взаимодействия.
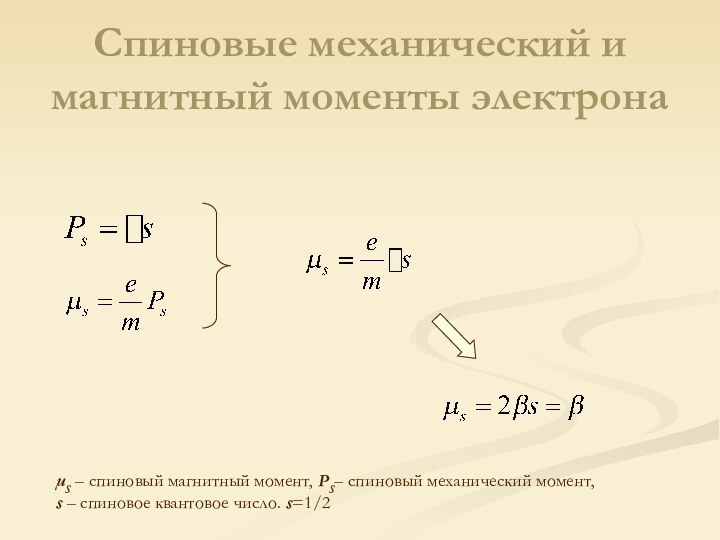
Слайд 14 S – спиновый магнитный момент, PS– спиновый механический
момент,
s – спиновое квантовое число. s=1/2
Спиновые механический и
магнитный моменты электрона
Слайд 15
Полные механический и магнитный моменты электрона
Полный магнитный момент
Полный
механический момент
Во многих случаях, орбитальный магнитный момент равен нулю.
Поэтому при обсуждении принципа метода ЭПР рассматривается только спиновый магнитный момент.
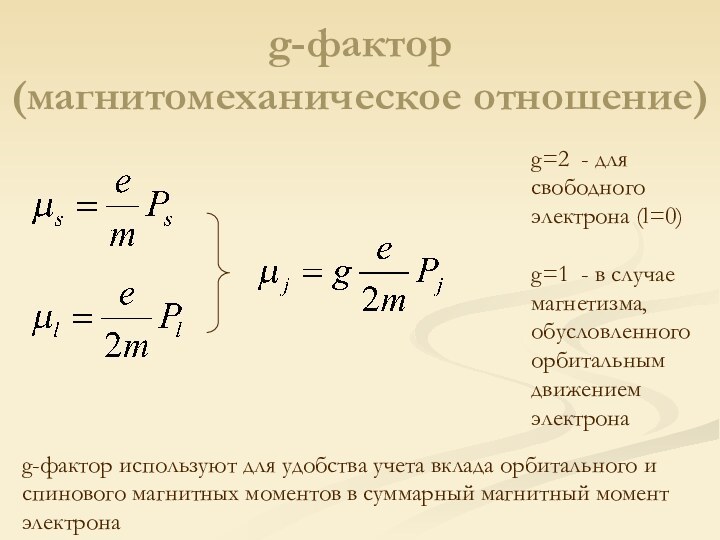
Слайд 16
g-фактор
(магнитомеханическое отношение)
g-фактор используют для удобства учета вклада
орбитального и спинового магнитных моментов в суммарный магнитный момент
электронаg=2 - для свободного электрона (l=0)
g=1 - в случае магнетизма, обусловленного орбитальным движением электрона
Слайд 17
Орбитальные и спиновые моменты атомов с несколькими электронами
g-фактор
может быть выражен через полные квантовые числа S, L,
Jмагнитные свойства атома определяются значениями квантовых чисел S, L, J
Слайд 18
Явление ЭПР
Физическая картина явления
Явление магнитного резонанса можно объяснить
в рамках классической и квантовой физики.
Слайд 19
Квантовомеханическая интерпретация ЭПР
Для выяснения физической картины явления ЭПР
рассмотрим, каким образом постоянное магнитное поле Н0 и переменное
магнитное поле H1(t) влияют на энергетические уровни изолированного парамагнитного атома.Магнитные свойства атома характеризуются значением квантового числа J — результирующего магнитного момента.
В большинстве химических и биологических систем, исследуемых методом ЭПР, орбитальные магнитные моменты L парамагнитных центров, как правило, либо равны нулю, либо практически не дают вклада в регистрируемые сигналы ЭПР, тогда будем считать, что парамагнитные свойства определяются суммарным спином атома S.
При отсутствии внешнего магнитного поля энергия свободного атома не зависит от ориентации спина. При включении внешнего магнитного поля Н0 происходит расщепление уровня энергии на 2S + 1 подуровней, соответствующих различным проекциям суммарного спина S в направлении вектора Н0 .
Слайд 20
Эффект Зеемана
H0
E
H
Расщепление энергетических уровней электронов в магнитном поле
H=0
В общем случае
Энергия взаимодействия магнитного момента электрона с магнитным
полем ms – магнитное спиновое квантовое число ms=-s,…, s, ml – магнитное орбитальное квантовое число, ml=-l,…,0,…l
В большинстве случаев электронные орбитали сильно отличаются от сферических, поэтому орбитальный магнитный момент дает относительно небольшой вклад в полный магнитный момент. Для упрощения вычислений этим вкладом можно пренебречь.
Н=0
Полный магнитный момент в проекции на выделенное направление, определяемое внешним магнитным полем
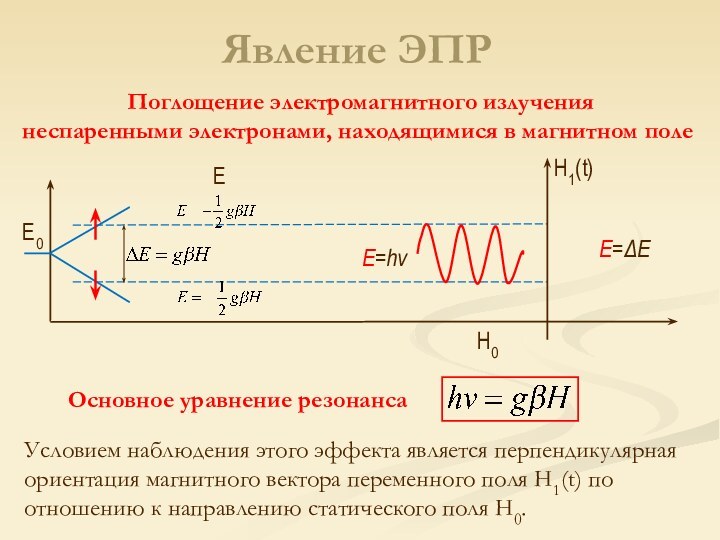
Слайд 21
Явление ЭПР
Поглощение электромагнитного излучения
неспаренными электронами, находящимися в магнитном
поле
E
H0
E0
E=h
Условием наблюдения этого эффекта является перпендикулярная ориентация магнитного вектора
переменного поля H1(t) по отношению к направлению статического поля H0. H1(t)
E=ΔE
Основное уравнение резонанса
Слайд 22
Принцип метода ЭПР
В основе метода ЭПР лежит
явление ЭПР
Если энергия квантов электромагнитного излучения, действующего на систему
спинов во внешнем магнитном поле, равна разности энергий между соседними уровнями, то такое излучение будет вызывать переходы между энергетическими уровнями.Если H1(t) Н0, вероятности индуцированных переходов как снизу вверх, так и сверху вниз одинаковы. Такие индуцированные переходы сопровождаются изменением ориентации спинов.
Согласно квантово-механическим правилам отбора, возможны лишь такие переходы (разрешенные), при которых значение магнитного квантового числа изменяется на величину mS = ± 1.
Переход с нижнего уровня на верхний сопровождается поглощением кванта электромагнитного излучения. Переход с верхнего уровня на нижний приводит к излучению кванта с энергией h .
E=h
Слайд 23 Согласно распределению Больцмана у парамагнетиков в состоянии термодинамического
равновесия заселенности нижнего и верхнего энергетических уровней различаются.
h
= 6,62*10-34Дж*с – постоянная Планка, k=1,38*10-23 Дж/К — постоянная Больцмана, Т — абсолютная температура, ns=-1/2 – число электронов с s=-1/2, ns=1/2 – число электронов с s=1/2Т.к. ns=1/2 / ns=-1/2 < 1, электромагнитное излучение будет чаще индуцировать переходы снизу вверх (поглощение энергии), чем переходы сверху вниз (излучение энергии). Поэтому в целом будет наблюдаться поглощение энергии электромагнитного поля парамагнитным образцом.
Разность энергий соседних зеемановских уровней: E = h kT, частота излучения соответствует микроволновому или радиочастотному диапазону (Х ~ 3 см (~ 1010 Гц) при H0 ~ = 3300 Гс).
ns=1/2
ns=-1/2
Слайд 24
Суть явления магнитной релаксации:
парамагнитные частицы могут обмениваться энергией
друг с другом;
парамагнитные частицы могут взаимодействовать с окружающими их
атомами и молекулами.Благодаря быстрой безызлучательной релаксации спинов в системе восстанавливается практически равновесное соотношение заселенностей зеемановских подуровней, при котором заселенность нижнего уровня выше заселенности верхнего уровня (ns=1/2 / ns=-1/2 < 1).
Число индуцированных переходов снизу вверх, отвечающих поглощению энергии, будет всегда превышать число индуцированных переходов сверху вниз, то есть резонансное поглощение энергии электромагнитного излучения будет превалировать над излучением.
Явление магнитной релаксации
Слайд 25
Классическая интерпретация ЭПР
M совершает круговые вращения по образующей
конуса с ларморовской частотой
Прецессия магнитного момента M парамагнетика в
постоянном магнитном поле H0 Допустим, парамагнитные свойства образца определяются магнитными моментами i входящих в него частиц, например, магнитных моментов неспаренных электронов (0) парамагнитных атомов или молекул
Если Н00, уравнение движения M имеет вид:
Если Н0=0, M ориентированы хаотически
Если H1 (t) H0 , H1 H0 , 1=21 , возникает дополнительный момент
??=??0.
Если 1≠L , суммарный дополнительный момент =0
Если 1=L (резонанс) , то векторы M(t) и H(t) будут вращаться синхронно 1, и абсолютная величина дополнительного момента ≠0. Под действием переменного поля угол прецессии станет периодически изменяться: вектор намагниченности M(t) будет то приближаться к плоскости (xy), то удаляться от нее.
Слайд 26 E = - (M Н) =
-| M | | Н | cos .
Если не учитывать процессы магнитной релаксации, то оказывается, что в течение полупериода, когда вектор M(t) приближается по направлению к вектору внешнего магнитного поля Н0 (угол прецессии уменьшается), энергия парамагнетика уменьшается и излучается образцом, а во время следующего полупериода (угол прецессии увеличивается) энергия парамагнетика увеличивается за счет поглощения энергии переменного магнитного поля H1(t).
Казалось бы, в целом парамагнитный образец не должен поглощать энергию электромагнитного излучения. Однако спины могут безызлучательно (в виде тепла) отдавать поглощаемую ими энергию решетке, в результате чего резонансное поглощение энергии будет преобладать над излучением.
Энергия магнитного момента M во внешнем магнитном поле
Слайд 27 Условием резонансного поглощения энергии электромагнитного излучения является не
только равенство частот 1 и с L, но и
совпадение направления круговой поляризации переменного поля H1(t) с направлением прецессии вектора намагниченности M(t) в поле Н0.На практике пользуются линейно поляризованным электромагнитным излучением, которое всегда можно представить в виде суперпозиции двух излучений одинаковой частоты, поляризованных по кругу, но вращающихся в разные стороны. Спектрометры ЭПР устроены так, что с образцом взаимодействует только правильно поляризованная компонента.
Так можно объяснить явление ЭПР в рамках классической физики
Слайд 28
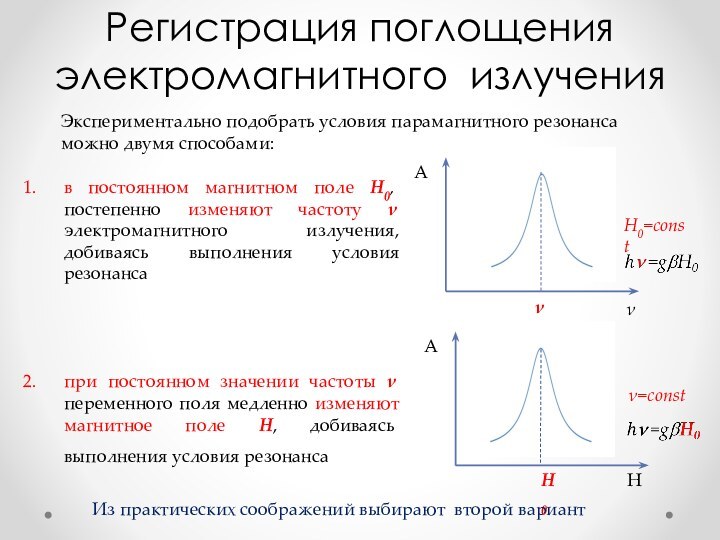
Устройство радиоспектрометра ЭПР
Экспериментально подобрать условия парамагнитного резонанса можно
двумя способами:
образец помещают в постоянное магнитное поле Н0, можно
затем постепенно изменять частоту электромагнитного излучения. По достижении резонансной частоты образец начнет поглощать энергию. при постоянном значении частоты переменного поля медленно изменяют магнитное поле, добиваясь выполнения условия резонанса h= gНрез.
Слайд 29
Регистрация поглощения электромагнитного излучения
в постоянном магнитном поле Н0,
постепенно изменяют частоту электромагнитного излучения, добиваясь выполнения условия
резонансапри постоянном значении частоты переменного поля медленно изменяют магнитное поле Н, добиваясь выполнения условия резонанса
H
A
A
H0=const
=const
Н0
Экспериментально подобрать условия парамагнитного резонанса можно двумя способами:
Из практических соображений выбирают второй вариант
Слайд 30
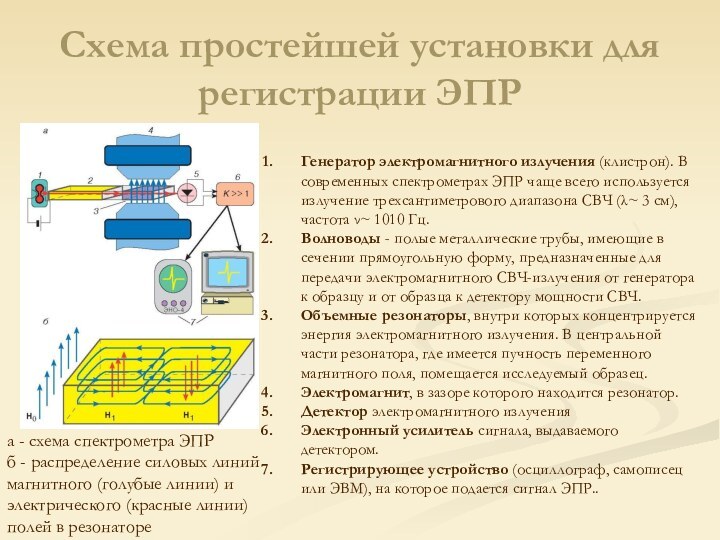
Схема простейшей установки для регистрации ЭПР
а -
схема спектрометра ЭПР
б - распределение силовых линий магнитного (голубые
линии) и электрического (красные линии) полей в резонаторе Генератор электромагнитного излучения (клистрон). В современных спектрометрах ЭПР чаще всего используется излучение трехсантиметрового диапазона СВЧ (~ 3 см), частота ~ 1010 Гц.
Волноводы - полые металлические трубы, имеющие в сечении прямоугольную форму, предназначенные для передачи электромагнитного СВЧ-излучения от генератора к образцу и от образца к детектору мощности СВЧ.
Объемные резонаторы, внутри которых концентрируется энергия электромагнитного излучения. В центральной части резонатора, где имеется пучность переменного магнитного поля, помещается исследуемый образец.
Электромагнит, в зазоре которого находится резонатор.
Детектор электромагнитного излучения
Электронный усилитель сигнала, выдаваемого детектором.
Регистрирующее устройство (осциллограф, самописец или ЭВМ), на которое подается сигнал ЭПР..
Слайд 31
Спектр ЭПР
Спектр поглощения
Спектр ЭПР
Сигнал ЭПР представляет собой
первую производную от линии поглощения dA/dH
A
dA/dH
H
H
H0
Слайд 32
Основные характеристики спектров ЭПР
Амплитуда
сигнала (A)
2. Ширина спектральной линии (H)
3. g-Фактор
H
A
Слайд 33 где Cx. и C0 - концентрации измеряемого образца
и эталона соответственно, а Sx и S0 - площади
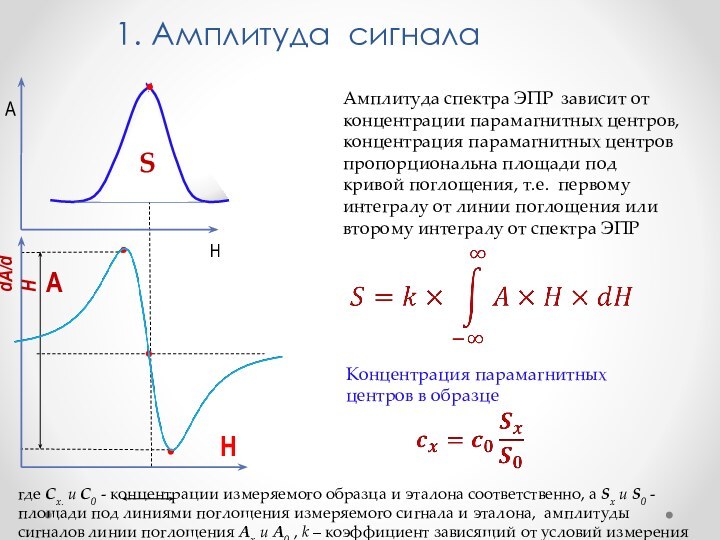
под линиями поглощения измеряемого сигнала и эталона, амплитуды сигналов линии поглощения Ax и A0 , k – коэффициент зависящий от условий измерения1. Амплитуда сигнала
H
A
Амплитуда спектра ЭПР зависит от концентрации парамагнитных центров, концентрация парамагнитных центров пропорциональна площади под кривой поглощения, т.е. первому интегралу от линии поглощения или второму интегралу от спектра ЭПР
Концентрация парамагнитных центров в образце
A
S
H
dA/dH
Слайд 34 (концентрация парамагнитных центров пропорциональна первому интегралу под линией
поглощения или второму интегралу от спектра ЭПР)
в точках
- и т.к.
Интегральная сумма
Очевидно, что при больших n (т.е. вдали от центра сигнала) вклад удаленных частей спектра может быть достаточно большим даже при малых значениях амплитуды сигнала.
поля где f’(H) - первая производная линии поглощения (спектр ЭПР), F(H) - функция линии поглощения,
H - напряженность магнитного, Hi - шаг изменения магнитного поля, а ni - номер шага.
Расчет площади под линией поглощения неизвестного сигнала
с использованием приема численного интегрирования
Слайд 35
Форма линии
Если можно пренебречь взаимодействием между парамагнитными частицами
( в разбавленных растворах) кривая поглощения описывается функцией Лоренца:
FL0 - функция кривой поглощения в точке резонанса, H0 - значение поля в точке резонанса, H1/2 - ширина сигнала на половине высоты. Аналогичные обозначения используются для кривой поглощения, описываемой функцией Гаусса.
Eсли между парамагнитными частицами существует взаимодействие кривая поглощения описывается функцией Гаусса
Функция Лоренца имеет более медленное убывание и более широкие крылья, что может давать значительную ошибку при интегрировании спектра.
Спектр ЭПР является непрерывным в некоторой окрестности точки резонанса.
Учитывать форму линии особенно важно при определении площади под кривой поглощения
Слайд 36
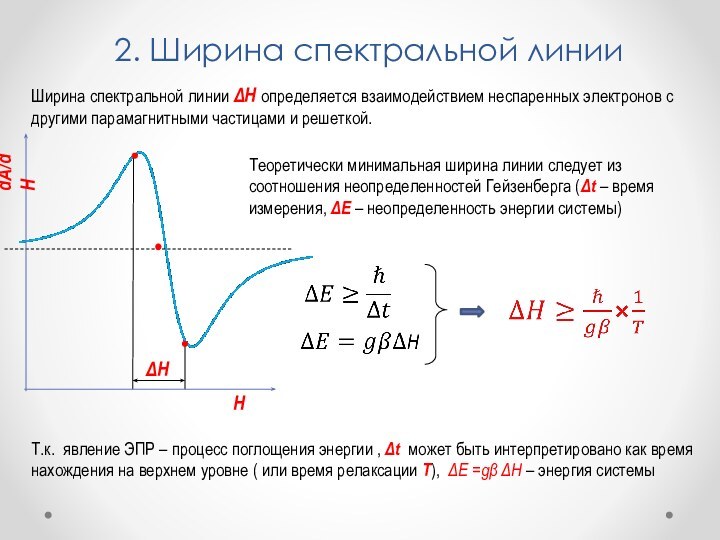
2. Ширина спектральной линии
Ширина спектральной линии H определяется
взаимодействием неспаренных электронов с другими парамагнитными частицами и решеткой.
H
dA/dH
H
Теоретически минимальная ширина линии следует из соотношения неопределенностей Гейзенберга (Δt – время измерения, ΔE – неопределенность энергии системы)
Т.к. явление ЭПР – процесс поглощения энергии , Δt может быть интерпретировано как время нахождения на верхнем уровне ( или время релаксации T), ΔE =g ΔH – энергия системы
Слайд 37
Время релаксации
Времена релаксации Т1 и Т2 зависят от
природы
парамагнитных центров
окружения
молекулярной подвижности
температуры
Спин-решеточная релаксация (T1 ) обусловлена взаимодействием
магнитного момента электрона с решеткой (средой) Спин-спиновая релаксация (Т2 ) обусловлена взаимодействием между магнитными моментами электронов (между спинами)
Релаксация – процесс восстановления заселенности энергетических уровней после поглощения кванта электромагнитного излучения. Механизм релаксации заключается в передаче кванта электромагнитной энергии решетке или окружающим электронам и возвращении электрона на низкоэнергетический уровень
Время релаксации – время нахождения на более высоком энергетическом уровне – определяется двумя процессами: спин-решеточной релаксацией и спин-спиновой релаксацией
Слайд 38
Ширина спектральной линии и время релаксации
Ширина одиночной линии
H обратно пропорциональна времени релаксации T:
T1=1 нс
H=10мТ
Комплексы металлов
T1=0,1 мс
H=100
мкТСвободные радикалы
H
H
Слайд 39
Механизмы уширения сигнала ЭПР
Взаимодействие магнитных моментов двух парамагнитных
частиц (радикалов или ионов) приводит к уширению по диполь-
дипольному механизмуВзаимодействие спинового магнитного момента электрона с орбитальным магнитным моментом электрона приводит к уширению сигнала в результате анизотропии g-фактора
Взаимное превращение форм радикала вызывает динамическое уширение сигнала
Соударение радикала с другим радикалом или парамагнитным ионом лежит в основе уширения за счет спинового обмена
(J – обменный интеграл)
S
l
’S
’’S
’’S
’S
J
R1R2
Слайд 40
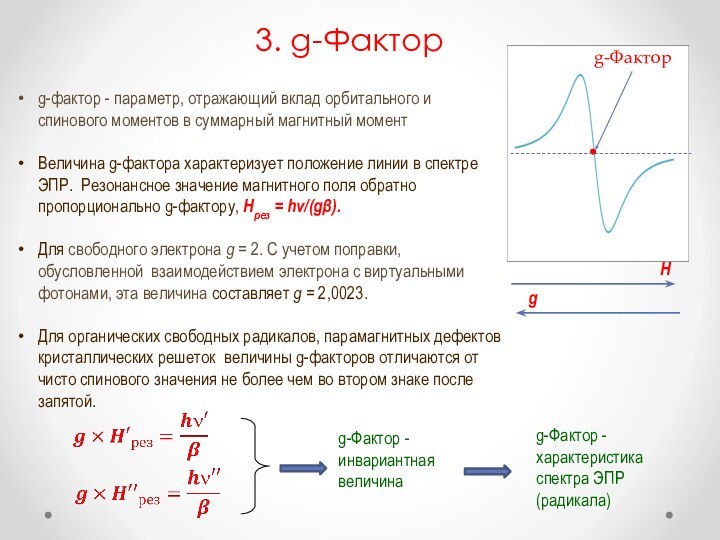
3. g-Фактор
g-фактор - параметр, отражающий вклад орбитального
и спинового моментов в суммарный магнитный момент
Величина g-фактора характеризует
положение линии в спектре ЭПР. Резонансное значение магнитного поля обратно пропорционально g-фактору, Нрез = hv/(g). Для свободного электрона g = 2. С учетом поправки, обусловленной взаимодействием электрона с виртуальными фотонами, эта величина составляет g = 2,0023.
Для органических свободных радикалов, парамагнитных дефектов кристаллических решеток величины g-факторов отличаются от чисто спинового значения не более чем во втором знаке после запятой.
g-Фактор -
инвариантная величина
g-Фактор -
характеристика спектра ЭПР (радикала)
Н
g
g-Фактор
Слайд 41
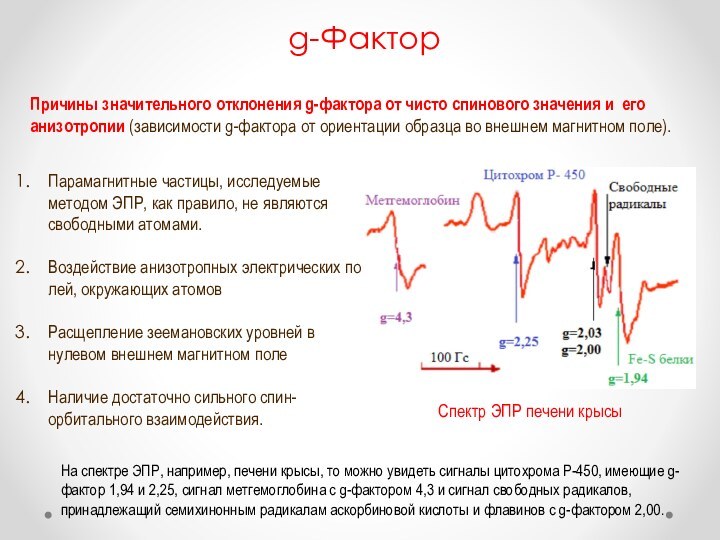
g-Фактор
Причины значительного отклонения g-фактора от чисто спинового значения
и его анизотропии (зависимости g-фактора от ориентации образца во
внешнем магнитном поле).Парамагнитные частицы, исследуемые методом ЭПР, как правило, не являются свободными атомами.
Воздействие анизотропных электрических полей, окружающих атомов
Расщепление зеемановских уровней в нулевом внешнем магнитном поле
Наличие достаточно сильного спин-орбитального взаимодействия.
Спектр ЭПР печени крысы
На спектре ЭПР, например, печени крысы, то можно увидеть сигналы цитохрома Р-450, имеющие g-фактор 1,94 и 2,25, сигнал метгемоглобина с g-фактором 4,3 и сигнал свободных радикалов, принадлежащий семихинонным радикалам аскорбиновой кислоты и флавинов с g-фактором 2,00.
Слайд 42
Сверхтонкое взаимодействие
Атомные ядра, у которых нечетно хотя бы
одно из двух чисел — масса или порядковый номер, — обладают
отличным от нуля моментом количества движения, т. е. ядерным спином.Ненулевым ядерным магнитным моментом обладают ядра: 1Н, 2Н, 13С, 14N, 15N, 19F, 29Si, 31P и др.
Для веществ, у которых ядерный спин J= 1/2 : 1H, 13C, 15N, 19F, 29Si, 31P , в поле возможны две ориентации магнитного момента ядра - "по полю" и "против поля"
Для веществ, у которых ядерный спин J= 1: 2Н, 14N (число протонов и нейтронов нечетные)- в поле возможны три ориентации магнитного момента ядра - "по полю" и "против поля" и перпендикулярно полю
Если кроме неспаренных электронов исследуемый парамагнитный образец содержит атомные ядра, обладающие собственными магнитными моментами, то за счет взаимодействия электронных и ядерных магнитных моментов (сверхтонкое взаимодействие) возникает сверхтонкая структура (СТС) спектра ЭПР
Слайд 43
Спин и магнитный момент ядра
Ядро атома будет иметь
ненулевой магнитный момент, в том случае, если число протонов
или число нейтронов (или оба), будут нечетные.J
J
J
J
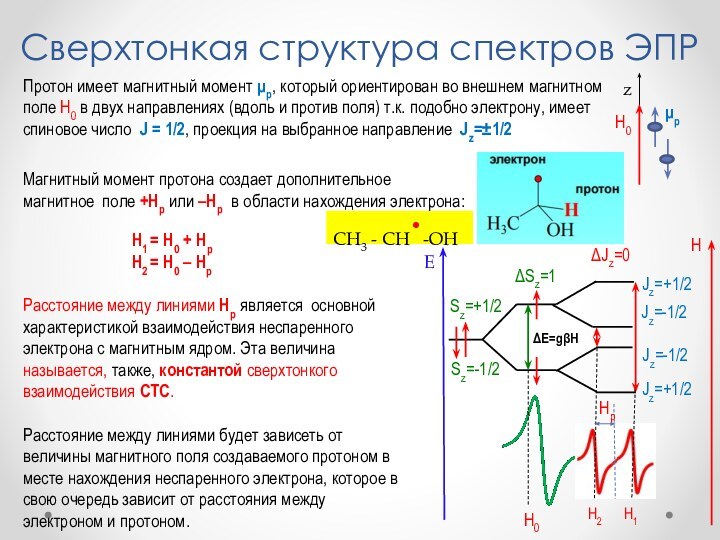
Слайд 44 Протон имеет магнитный момент p, который ориентирован во
внешнем магнитном поле H0 в двух направлениях (вдоль и
против поля) т.к. подобно электрону, имеет спиновое число J = 1/2, проекция на выбранное направление Jz=1/2H1 = H0 + Hp
H2 = H0 – Hp
=gH
Sz=-1/2
Sz=+1/2
Sz=1
Jz=0
Jz=+1/2
Jz=+1/2
Jz=-1/2
Jz=-1/2
H
E
H1
H2
H0
CH3 - CH•-OH
Магнитный момент протона создает дополнительное магнитное поле +Hp или –Hp в области нахождения электрона:
z
Hp
Расстояние между линиями Нр является основной характеристикой взаимодействия неспаренного электрона с магнитным ядром. Эта величина называется, также, константой сверхтонкого взаимодействия СТС.
Расстояние между линиями будет зависеть от величины магнитного поля создаваемого протоном в месте нахождения неспаренного электрона, которое в свою очередь зависит от расстояния между электроном и протоном.
H0
p
Сверхтонкая структура спектров ЭПР
Слайд 45
Сверхтонкая структура спектров ЭПР
Неспаренный электрон в радикале может
быть расположен близко к двум протонам, как в радикале
этанолаCH2• - CH2 - OH
Магнитное поле вокруг неспаренного электрона теперь
может иметь следующие значения:
Н1 = H0 + Hp1 + Hp2 = H0 + 2Нр
H2 = H0 + Hp1 – Hp2 = H0
H2 = H0 – Hp1 + Hp2 = H0
H3 = H0 – Hp1 – Hp2 = H0 – 2Нр
Состояние Н2=Н0 реализуется двумя способами следовательно вероятность этого состояния
и интенсивность сигнала будут вдвое больше чем вероятность состояний Н1=Н0+2Нр или Н3=Н0-2Нр , реализуемых одним способом.
Т.обр., вместо одного сигнала будет три с соотношением интенсивностей 1:2:1
В данном случае константа СТС равна 2Нр
2Нр
2Нр
Слайд 46
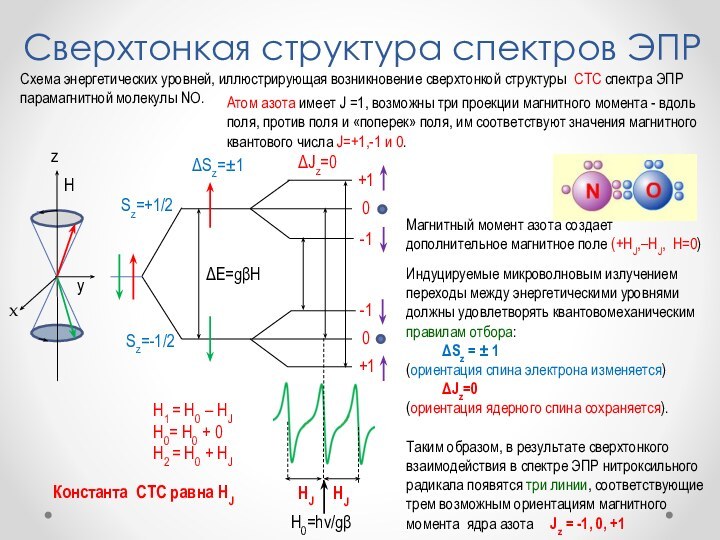
Сверхтонкая структура спектров ЭПР
H
z
x
y
Sz=+1/2
Sz=-1/2
Sz=1
=gH
+1
Jz=0
0
0
+1
-1
-1
H0=h/g
Схема энергетических уровней, иллюстрирующая возникновение
сверхтонкой структуры СТС спектра ЭПР парамагнитной молекулы NO.
Индуцируемые
микроволновым излучением переходы между энергетическими уровнями должны удовлетворять квантовомеханическим правилам отбора: Sz = ± 1
(ориентация спина электрона изменяется)
Jz=0
(ориентация ядерного спина сохраняется).
Таким образом, в результате сверхтонкого взаимодействия в спектре ЭПР нитроксильного радикала появятся три линии, соответствующие трем возможным ориентациям магнитного момента ядра азота Jz = -1, 0, +1
H1 = H0 – HJ
H0= H0 + 0
H2 = H0 + HJ
Атом азота имеет J =1, возможны три проекции магнитного момента - вдоль поля, против поля и «поперек» поля, им соответствуют значения магнитного квантового числа J=+1,-1 и 0.
Магнитный момент азота создает дополнительное магнитное поле (+HJ,–HJ, Н=0)
HJ
Константа СТС равна HJ
HJ
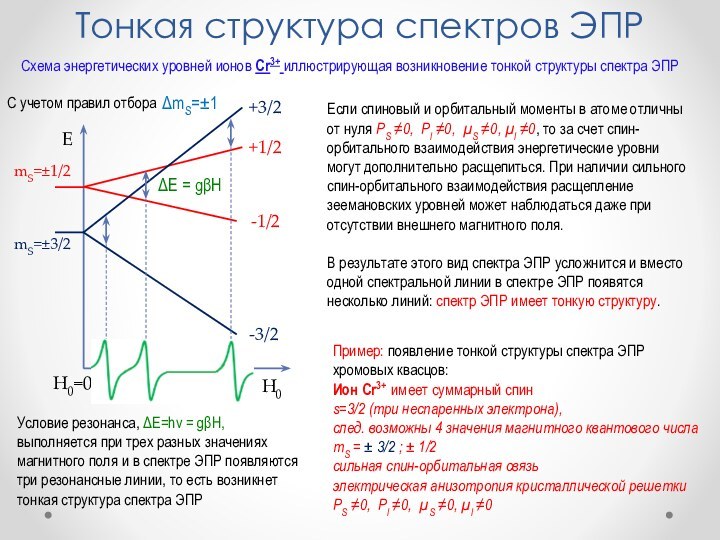
Слайд 47
Тонкая структура спектров ЭПР
Если спиновый и орбитальный моменты
в атоме отличны от нуля PS ≠0, Pl ≠0,
S ≠0, l ≠0, то за счет спин-орбитального взаимодействия энергетические уровни могут дополнительно расщепиться. При наличии сильного спин-орбитального взаимодействия расщепление зеемановских уровней может наблюдаться даже при отсутствии внешнего магнитного поля.В результате этого вид спектра ЭПР усложнится и вместо одной спектральной линии в спектре ЭПР появятся несколько линий: спектр ЭПР имеет тонкую структуру.
mS=3/2
mS=1/2
H0
E
H0=0
-3/2
-1/2
+3/2
+1/2
Пример: появление тонкой структуры спектра ЭПР хромовых квасцов:
Ион Cr3+ имеет суммарный спин
s=3/2 (три неспаренных электрона),
след. возможны 4 значения магнитного квантового числа
mS = ± 3/2 ; ± 1/2
сильная спин-орбитальная связь
электрическая анизотропия кристаллической решетки
PS ≠0, Pl ≠0, S ≠0, l ≠0
mS=1
E = gH
Условие резонанса, E=hv = gH, выполняется при трех разных значениях магнитного поля и в спектре ЭПР появляются три резонансные линии, то есть возникнет тонкая структура спектра ЭПР
С учетом правил отбора
Схема энергетических уровней ионов Cr3+ иллюстрирующая возникновение тонкой структуры спектра ЭПР
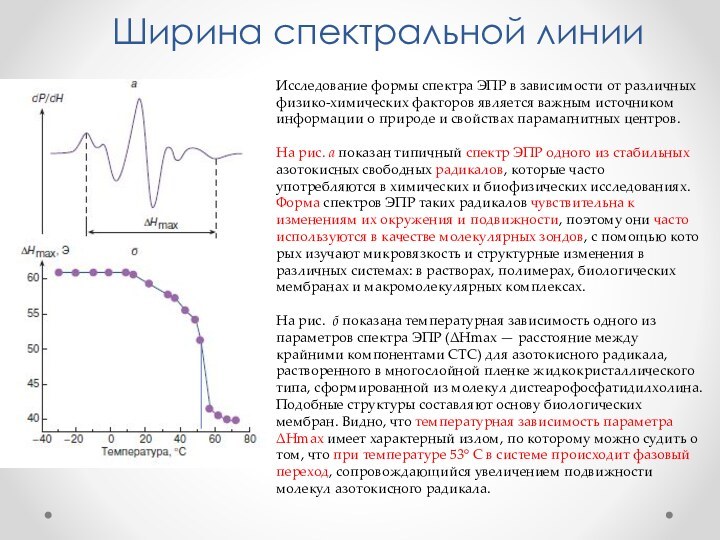
Слайд 48 Исследование формы спектра ЭПР в зависимости от различных
физико-химических факторов является важным источником информации о природе и
свойствах парамагнитных центров.На рис. а показан типичный спектр ЭПР одного из стабильных азотокисных свободных радикалов, которые часто употребляются в химических и биофизических исследованиях. Форма спектров ЭПР таких радикалов чувствительна к изменениям их окружения и подвижности, поэтому они часто используются в качестве молекулярных зондов, с помощью которых изучают микровязкость и структурные изменения в различных системах: в растворах, полимерах, биологических мембранах и макромолекулярных комплексах.
На рис. б показана температурная зависимость одного из параметров спектра ЭПР (Нmах — расстояние между крайними компонентами СТС) для азотокисного радикала, растворенного в многослойной пленке жидкокристаллического типа, сформированной из молекул дистеарофосфатидилхолина. Подобные структуры составляют основу биологических мембран. Видно, что температурная зависимость параметра Нmах имеет характерный излом, по которому можно судить о том, что при температуре 53° С в системе происходит фазовый переход, сопровождающийся увеличением подвижности молекул азотокисного радикала.
Ширина спектральной линии
Слайд 49 Перечисленные выше характеристики спектров ЭПР — g-фактор, тонкая
и сверхтонкая структура спектра ЭПР, ширины отдельных компонент спектра
— являются своего рода "паспортом" парамагнитного образца, по которому можно идентифицировать источник сигнала ЭПР и определить его физико-химические свойства.Так, например, наблюдая за сигналами ЭПР биологических объектов, можно непосредственно следить за ходом внутриклеточных процессов в листьях растений, тканях и клетках животных, в бактериях.
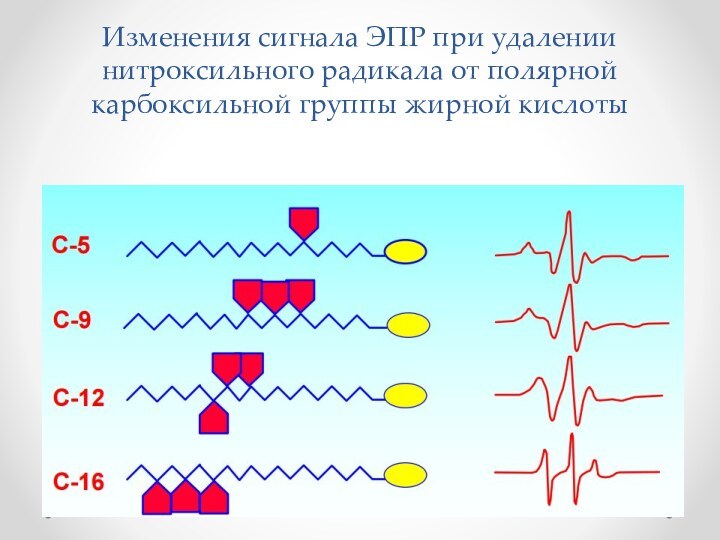
Слайд 60 Изменения сигнала ЭПР при удалении нитроксильного радикала от
полярной карбоксильной группы жирной кислоты
Слайд 64
Литература
1. Дж. Вертц и Дж. Болтон Теория и
практические
приложения метода ЭПР. Мир, Москва, 1975.
2. Современные методы биофизических
исследований.Практикум по биофизике. Под редакцией А.Б. Рубина.
Высшая школа, Москва, 1988.
3. Метод спиновых Меток. Теория и применение. Под
редакцией Л. Берлинера. Мир, Москва, 1979.
4. Кузнецов А.Н. Метод спинового зонда. Наука, Москва,
1976.
5. Зубарев В.Е. Метод спиновых ловушек. Издательство
МГУ, Москва, 1984.
Слайд 65
Вопросы к зачету
1. Магнитные свойства веществ. Орбитальный и
спиновый угловые моменты электрона.
2. Орбитальный и спиновый магнитный моменты
электрона. Соотношение между угловыми и магнитными моментами.3. Магнитный момент в магнитном поле. Зеемановское расщепление энергетических уровней. Взаимодействие магнитных моментов с электромагнитным излучением.
4. Принцип электронного парамагнитного резонанса.
5. Спин-решеточное и спин-спиновое взаимодействие. Времена спин-решеточной и спин-спиновой релаксации. Механизмы спин-решеточной и спин-спиновой релаксации.
6. Ширина линии поглощения. Связь ширины линии с временами спин-решеточной и спин-спиновой релаксации. Интенсивность линии. Определение концентрации парамагнитных частиц по интенсивности сигнала ЭПР.
7. Сверхтонкое взаимодействие электронов и ядер. Механизмы сверхтонкого взаимодействия. Сверхтонкая структура в спектрах ЭПР. Энергетические уровни неспаренных электронов при взаимодействии с ядрами с различными спинами. Эквивалентные и неэквивлентные ядра.
8. Изотропная и анизотропная сверхтонкая структура. Анализ сверхтонкой структуры. Проблемы регистрации разрешенных спектров ЭПР в биологических системах. Причины анизотропии спектров ЭПР: анизотропия сверхтонкого взаимодействия и g-фактора.
9. Применение ЭПР в биологии. Особенности биологических образцов.
10. Ранние эксперименты, проводившиеся на лиофильно высушенных и замороженных объектах, эксперименты на интактных объектах. Современные направления развития экспериментальной техники ЭПР.
11. Основные направления применения ЭПР в биологии. Примеры исследования радиобиологических, фотобиологических и ферментативных процессов.
Метод спиновых зондов и меток. Какие вещества применяются в качестве спиновых меток и зондов. Требования к их химическим свойствам. Особенности сигналов ЭПР зондов и меток. Применение зондов и меток в исследовании структурно-динамических свойств биомакромолекул и биомембран..
13. Принцип метода ядерного магнитного резонанса (ЯМР). Спины ядер.
14. Магнитный момент ядра. Поведение магнитного момента ядра в магнитном поле. Уравнение Лармора. Макроскопическая намагниченность.
15. Лабораторная и подвижная система координат. Эффективное магнитное поле. Спин-решеточная и спин-спиновая релаксация. Уравнения Блоха.
16. Стационарный и импульсный методы регистрации сигналов ЯМР. Импульсная Фурье - спектроскопия ЯМР. Импульсные методы регистрации времен спин-спиновой и спин-решеточной релаксации.
17. Ширина линии ЯМР. Связь ширины линии с временами спин-решеточной и спин-спиновой релаксации. Понятие о квадрупольной релаксации. Интенсивность сигналов ЯМР. Аппаратурные причины уширения линий.
18. Химический сдвиг. Природа химического сдвига . Составляющие химического сдвига. Примеры химических сдвигов различных ядер.
19. Спин-спиновое взаимодействие и его отражение в спектрах ЯМР.
20. Особенности сигналов ЯМР в жидкостях и твердых телах. Современные методы регистрации разрешенных спектров ЯМР в твердых телах. Двумерная спектроскопия ЯМР.
21. Основные направления использования ЯМР в биологии и медицине.
22. Применение ЯМР в изучении структурно-динамических свойств макромолекул и биомембран. ЯМР-томография.





























