- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Фазовые портреты динамических систем
Содержание
- 2. Зачем нужны фазовые портреты?
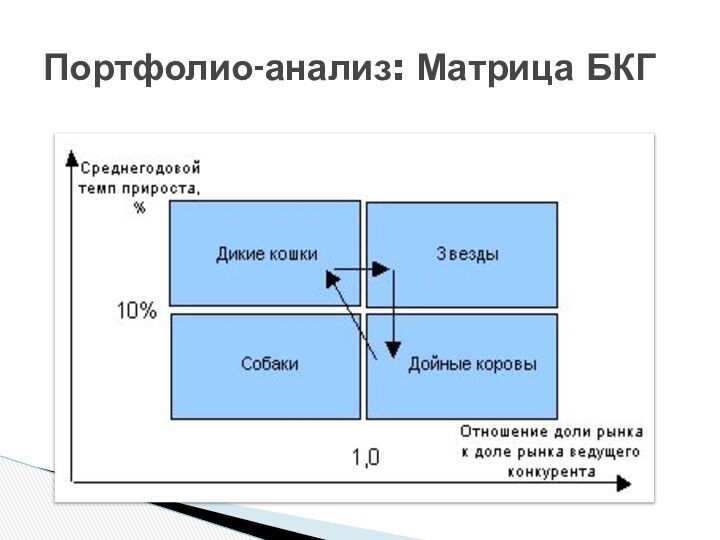
- 3. Портфолио-анализ: Матрица БКГ
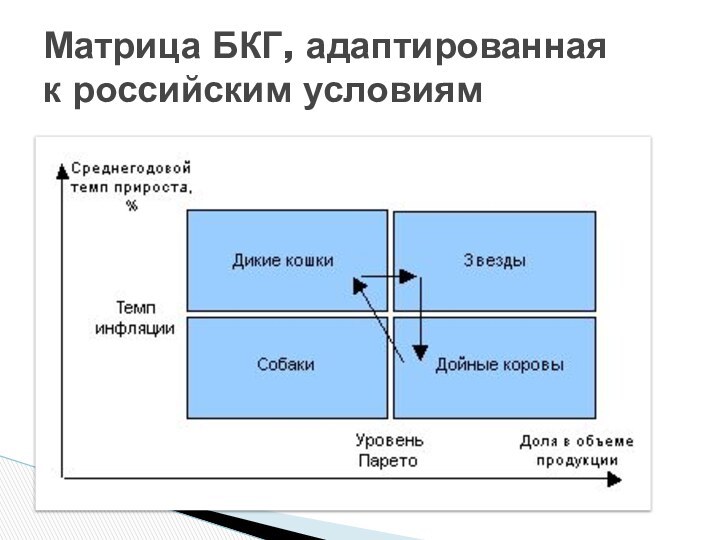
- 4. Матрица БКГ, адаптированная к российским условиям
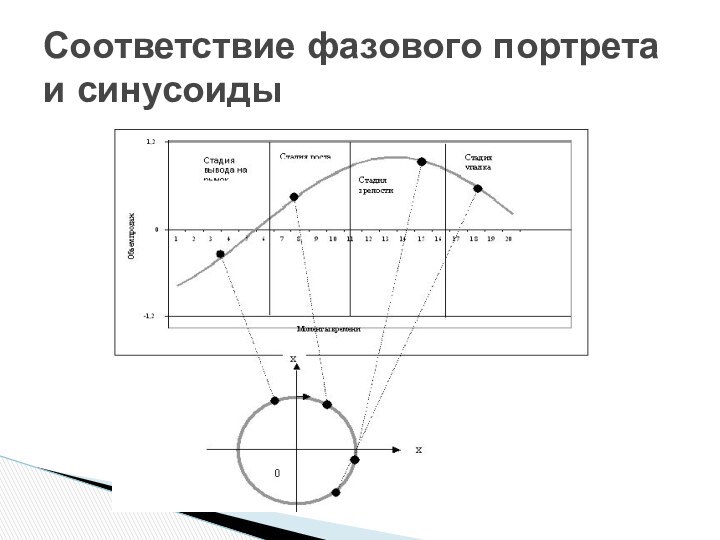
- 5. Соответствие фазового портрета и синусоиды
- 6. Предприниматели-пионеры (рудералы)Спонтанно имитирующие (конкуренты)Реагирующие под давлением (стресс-толеранты)Немобильные (стратегия выживания)Жизненный цикл фирм
- 7. Фазовый портрет ЖЦ фирм
- 8. Как строить фазовые портреты?
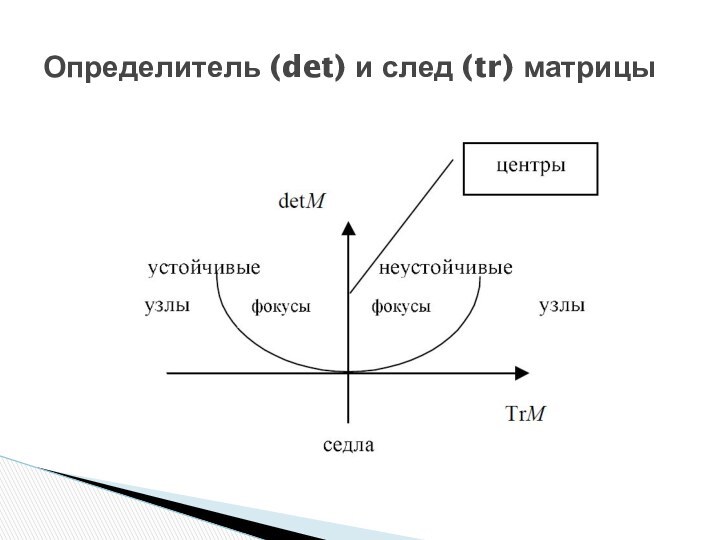
- 9. Определитель (det) и след (tr) матрицы.Характер особой
- 10. Общий вид системы уравнений
- 11. Определитель (det) и след (tr) матрицы
- 12. Определитель (det) и след (tr) матрицы
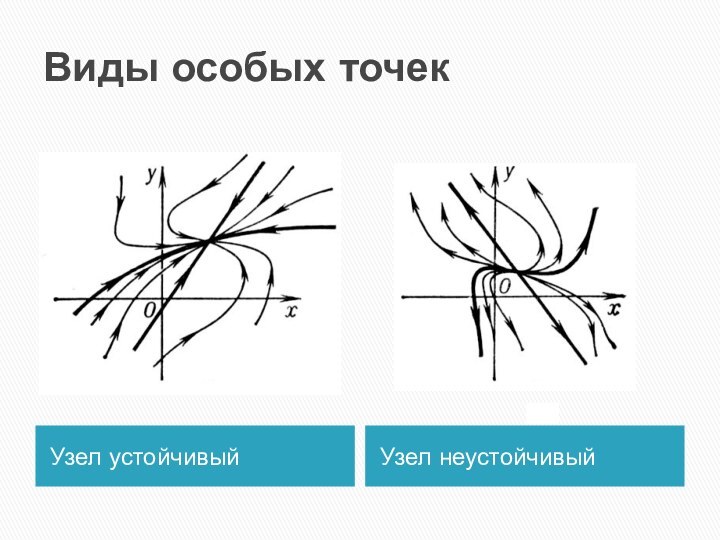
- 13. Виды особых точекУзел устойчивыйУзел неустойчивый
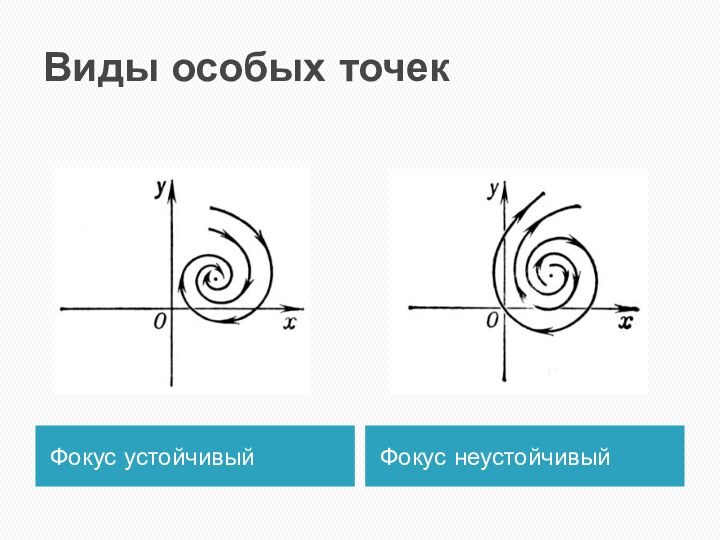
- 14. Виды особых точекФокус устойчивыйФокус неустойчивый
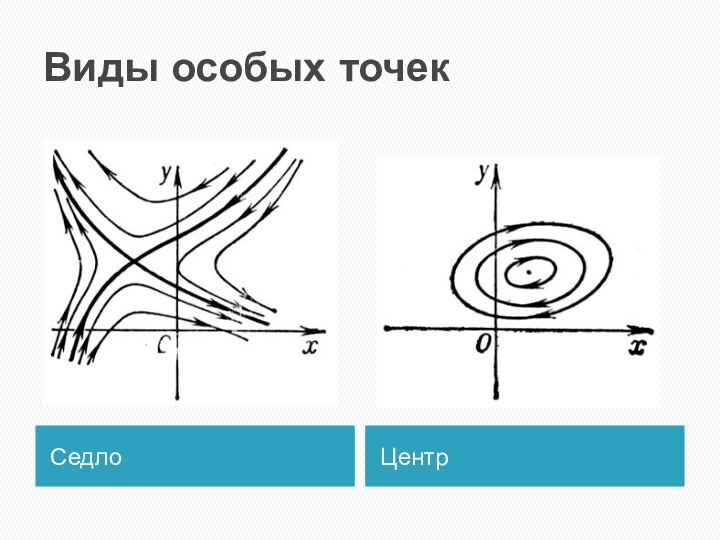
- 15. Виды особых точекСедлоЦентр
- 16. При ∆ = 0:
- 17. Асимптоты
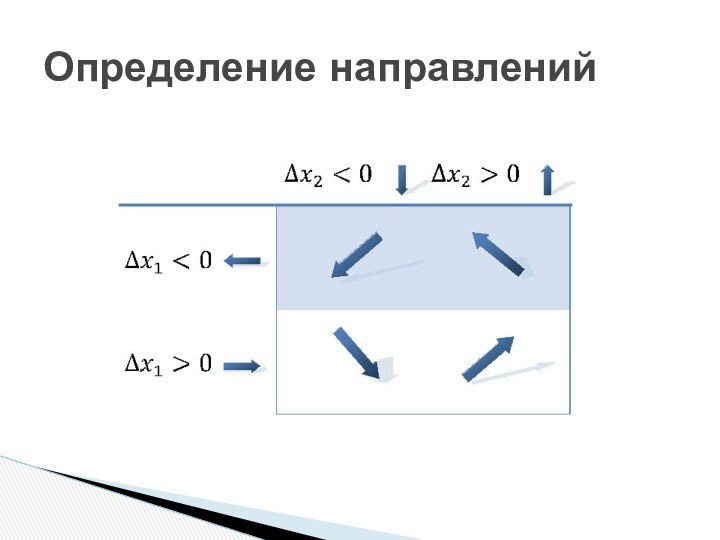
- 18. Определение направлений
- 19. Скачать презентацию
- 20. Похожие презентации
Зачем нужны фазовые портреты?











Слайд 6
Предприниматели-пионеры (рудералы)
Спонтанно имитирующие (конкуренты)
Реагирующие под давлением
(стресс-толеранты)
Немобильные (стратегия выживания)
Жизненный
цикл фирм
Слайд 9
Определитель (det) и след (tr) матрицы.
Характер особой точки
(по рисунку)
Особые направления (∆X = 0; ∆Y = 0).
Если
особая точка – седло или узел, найти асимптоты из принципа Y = k * X.Определить направление фазовых траекторий
Порядок построения
Слайд 16 При ∆ = 0:
особые направления перпендикулярны
2. При ∆
= 0:особые направления перпендикулярны
Особые направления