- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Физические основы функционирования гидросистем
Содержание
- 2. Основы гидростатикиГидростатикой называют раздел гидромеханики, в котором
- 3. Массовые силыМассовые силы пропорциональны массе выделенного объема
- 4. Поверхностные силыВ покоящейся жидкости поверхностные силы направлены по нормали к элементу поверхности выделенного объема.p -гидростатическое давление
- 5. Свойства гидростатического давленияГидростатическое давление действует нормально к
- 6. Закон Паскаля ☞Давление на поверхность жидкости, произведенное
- 7. Основное уравнение гидростатики Пусть на единицу массы
- 8. Уравнения ЭйлераЧасто их записывают в следующем виде:Или
- 9. Если уравнения системы умножить последовательно на dx,
- 10. Поверхность уровняЕсли вдоль какой-либо поверхности давление неизменное,
- 11. Равновесие несжимаемой жидкостиЕсли жидкость находится в равновесии
- 12. Или проинтегрировав
- 13. ОтсюдаУчитывая что
- 14. Относительное равновесие жидкостиОтносительным равновесием жидкости называется такое
- 15. Движение по вертикали с постоянным ускорением аПроекции
- 16. Поверхности равного давленияСоставим уравнение поверхности уровняЕсли g≠0
- 17. Горизонтальное перемещение резервуара с жидкостью с постоянным
- 18. Поверхность равного давления определится уравнением После интегрирования
- 19. Вращение цилиндрического сосуда с жидкостью с постоянной
- 20. Учитывая, что получим Откуда Т.о. при вращении сосуда
- 21. Закон распределения давления Закон распределения давления
- 22. Давление жидкости на плоские поверхностиСила давления на
- 23. Закон Архимеда Рассмотрим силы давления жидкости на
- 24. ДомкратВ машиностроении широко используется передача энергии и
- 25. МультипликаторПрименяется для повышения давления в отдельных элементах
- 26. Равновесие тел погруженных в жидкость На тело,
- 27. Для равновесия тела, плавающего на свободной поверхности,
- 28. ЗадачаКусок парафина объемом V находится между водой
- 29. Сила гидростатического давления на плоскую поверхность Сила
- 30. Итак сила избыточного давления Эта сила приложена
- 31. Сила гидростатического давления на криволинейную поверхность Сила
- 32. Горизонтальная составляющая Горизонтальная составляющая избыточного давления Рх
- 33. Вертикальная составляющая Вертикальная составляющая Рz равна весу
- 34. ЗадачаЗакрытый резервуар заполнен дизельным топливом, температура которого
- 35. Скачать презентацию
- 36. Похожие презентации























Слайд 3
Массовые силы
Массовые силы пропорциональны массе выделенного объема или
при постоянной плотности среды пропорциональны объему. Они действуют на
все частицы этого объема. Массовыми силами являются силы веса, силы инерции, электромагнитные силы.
Слайд 4
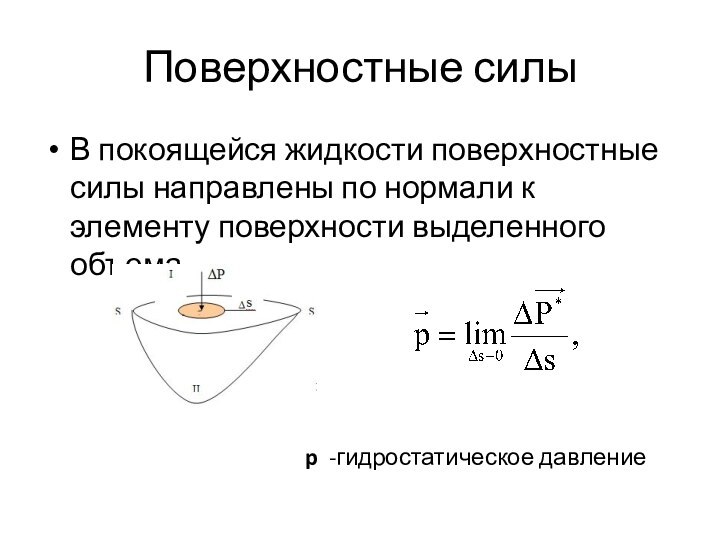
Поверхностные силы
В покоящейся жидкости поверхностные силы направлены по
нормали к элементу поверхности выделенного объема.
p -гидростатическое давление
Слайд 5
Свойства гидростатического давления
Гидростатическое давление действует нормально к площадке
действия и является сжимающим, т.е. оно направлено внутрь того
объема жидкости, который мы рассматриваем.Гидростатическое давление Р в любой точке одинаково по всем направлениям (т.е. не зависит от угла наклона площадки действия).
px=рn=рz=р
Слайд 6
Закон Паскаля
☞Давление на поверхность жидкости, произведенное внешними
силами, передается жидкостью одинаково во всех направлениях.
Очевидно, что
если давление не зависит от ориентации площадки, проходящей через данную точку, и определяется только положением точки в жидкости, то давление р есть функция только координат х, у, z, т. е. р = f (х,у,z).
Слайд 7
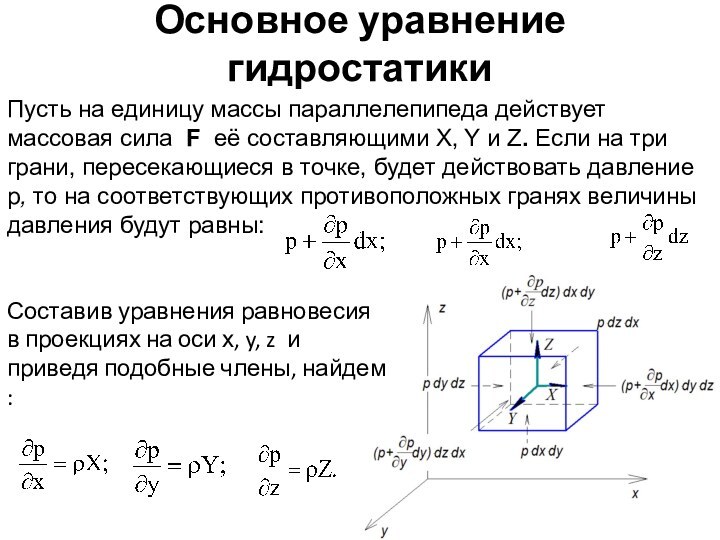
Основное уравнение гидростатики
Пусть на единицу массы параллелепипеда действует
массовая сила F её составляющими X, Y и Z.
Если на три грани, пересекающиеся в точке, будет действовать давление р, то на соответствующих противоположных гранях величины давления будут равны:Составив уравнения равновесия в проекциях на оси х, y, z и приведя подобные члены, найдем :
Слайд 9 Если уравнения системы умножить последовательно на dx, dy,
dz и сложить, то получим
откуда основное уравнение гидростатики:
Интегрируя
это уравнение и считая, что плотность ρ постоянна, получим что гидростатическое давление в любой точке жидкости будетр=ρ∫( Хdx+Ydy+Zdxz).
Слайд 10
Поверхность уровня
Если вдоль какой-либо поверхности давление неизменное, т.е.
р=const или dр=0, то такая жидкость называется поверхностью равного
давления или поверхностью уровня.или
Здесь принято, что
Т.е. массовые силы имеют потенциал и проекции массовых сил
представлены в виде:
Слайд 11
Равновесие несжимаемой жидкости
Если жидкость находится в равновесии под
действием собственного веса, то проекции ускорений вызванных силой тяжести
для выбранных координатных осей Х=0, Y=0, Z= -g, где g-ускорение свободного падения.Тогда подставляя эти значения в основное уравнение гидростатики, получим
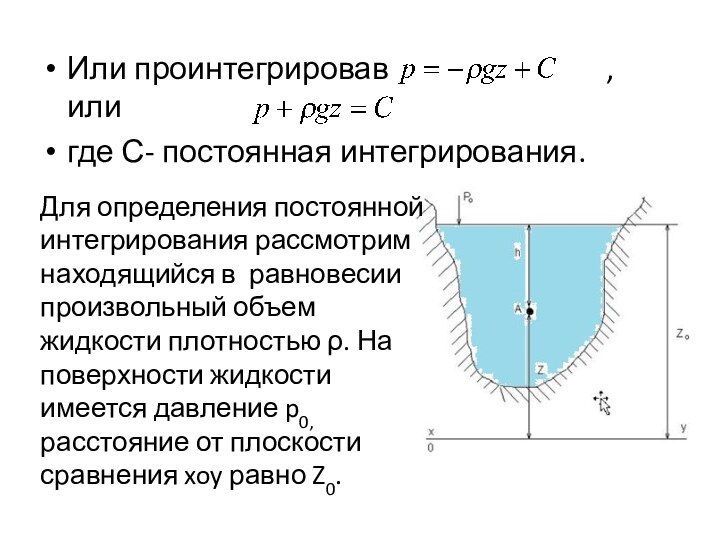
Слайд 12 Или проинтегрировав
,
илигде С- постоянная интегрирования.
Для определения постоянной интегрирования рассмотрим находящийся в равновесии произвольный объем жидкости плотностью ρ. На поверхности жидкости имеется давление p0, расстояние от плоскости сравнения xoy равно Z0.
Слайд 13
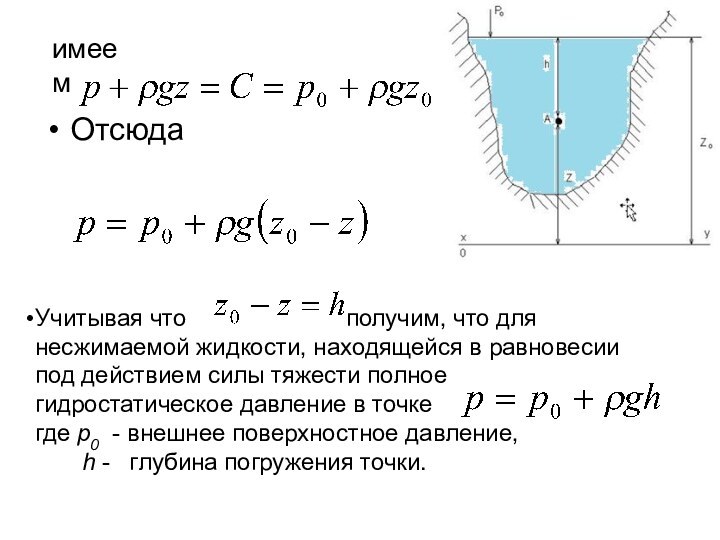
Отсюда
Учитывая что
получим, что для
несжимаемой жидкости, находящейся в равновесии под действием силы тяжести полное гидростатическое давление в точке где р0 - внешнее поверхностное давление,h - глубина погружения точки.
имеем
Слайд 14
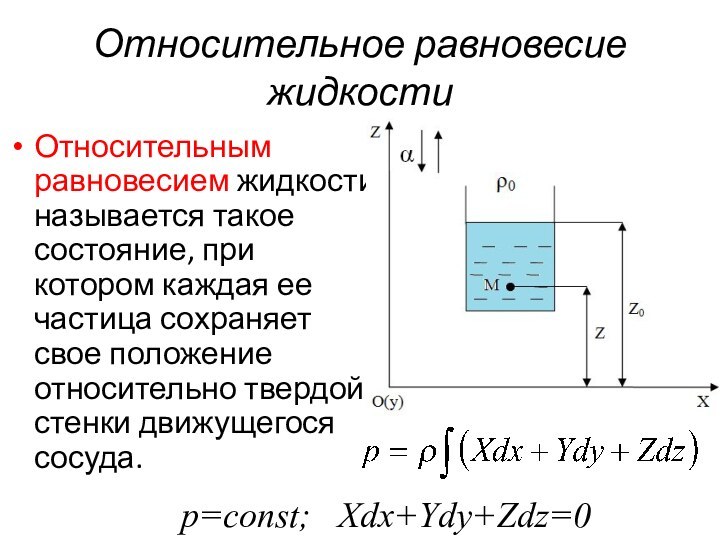
Относительное равновесие жидкости
Относительным равновесием жидкости называется такое состояние,
при котором каждая ее частица сохраняет свое положение относительно
твердой стенки движущегося сосуда.р=const; Xdx+Ydy+Zdz=0
Слайд 15
Движение по вертикали с постоянным ускорением а
Проекции массовых
сил на координатные оси будут:
X=0, Y=0, Z=-g+a. Знак
«-» соответствует равноускоренному подъему резервуара, «+»- спуску. Характер распределения давления получим следующий
где С- постоянная интегрирования, определяемая из граничных условий на свободной поверхности Z=Z0 и P=P0.
Тогда давление в любой точке, можно определять по формуле
Слайд 16
Поверхности равного давления
Составим уравнение поверхности уровня
Если g≠0 то
dz=0, а z=const, т.е. поверхности равного давления представляют собой
горизонтальные плоскости.Слайд 17 Горизонтальное перемещение резервуара с жидкостью с постоянным ускорением
а
В этом случае X = -a,
Y = 0, Z = -g. Закон распределения
давления получим в виде
После интегрирования
с учетом граничных
условий x=x0, z=z0, p=p0 получим закон распределения давления в следующем виде
Слайд 18
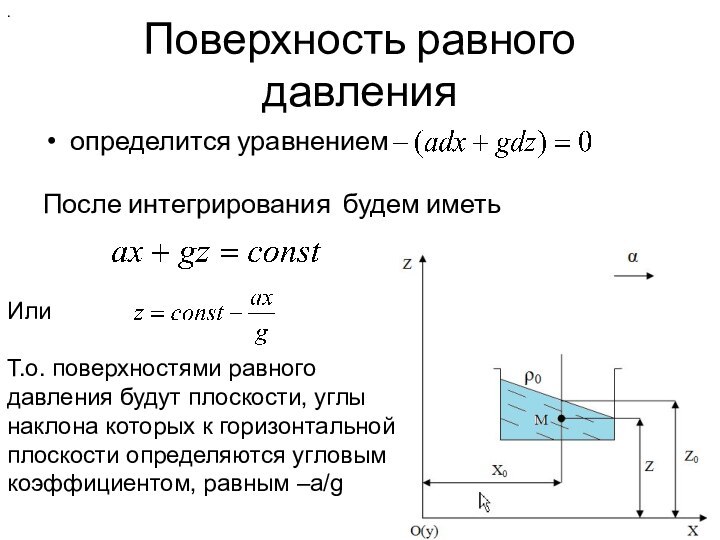
Поверхность равного давления
определится уравнением
После интегрирования будем
иметь
Или
Т.о. поверхностями равного давления будут плоскости, углы наклона которых к горизонтальной плоскости определяются угловым коэффициентом, равным –a/g
.
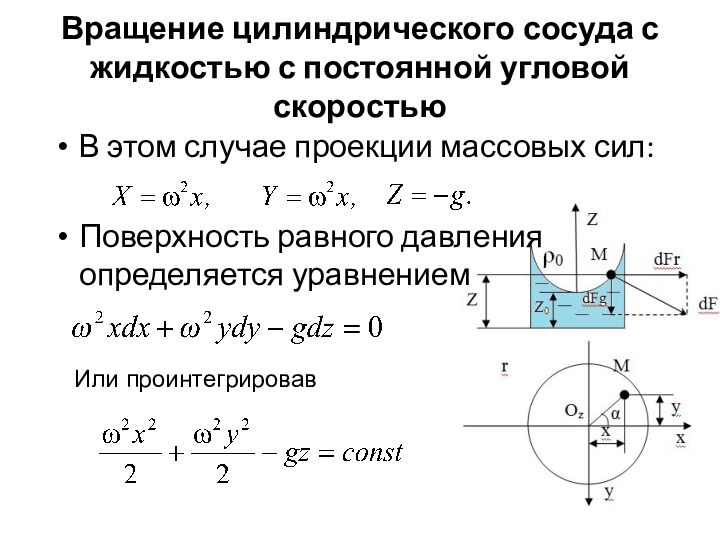
Слайд 19 Вращение цилиндрического сосуда с жидкостью с постоянной угловой
скоростью
В этом случае проекции массовых сил:
Поверхность равного давления
определяется уравнениемИли проинтегрировав
Слайд 20
Учитывая, что
получим
Откуда
Т.о. при вращении сосуда
с жидкостью вокруг вертикальной оси поверхностями равного давления будет
семейство параболоидов вращения, осью которых является ось Oz.
Слайд 21
Закон распределения давления
Закон распределения давления получим из
или
После интегрирования с учетом граничных условий r =0, z=z0,
p=p0 получим закон распределения давления:
Слайд 22
Давление жидкости на плоские поверхности
Сила давления на эту
площадку
.Равнодействующая сила давления определится так
Слайд 23
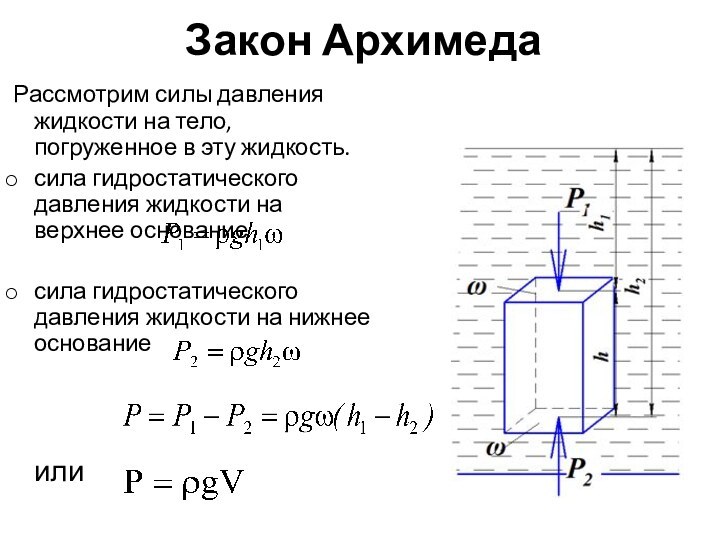
Закон Архимеда
Рассмотрим силы давления жидкости на тело,
погруженное в эту жидкость.
сила гидростатического давления жидкости на
верхнее основание сила гидростатического давления жидкости на нижнее основание
или
Слайд 24
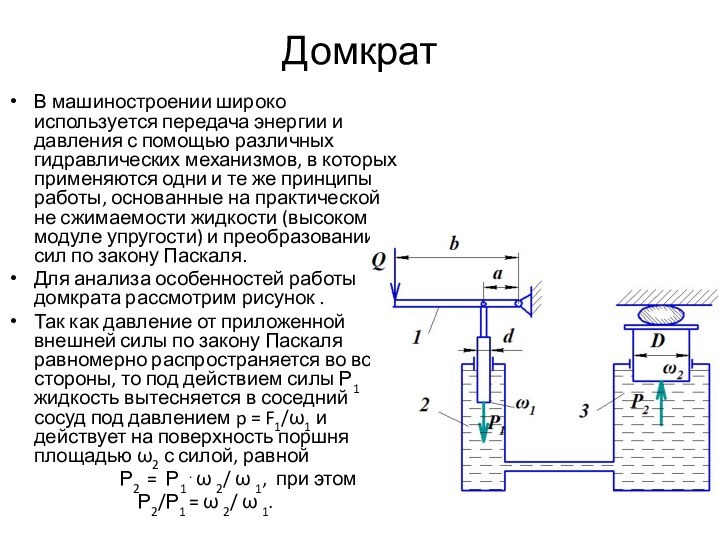
Домкрат
В машиностроении широко используется передача энергии и давления
с помощью различных гидравлических механизмов, в которых применяются одни
и те же принципы работы, основанные на практической не сжимаемости жидкости (высоком модуле упругости) и преобразовании сил по закону Паскаля.Для анализа особенностей работы домкрата рассмотрим рисунок .
Так как давление от приложенной внешней силы по закону Паскаля равномерно распространяется во все стороны, то под действием силы Р1 жидкость вытесняется в соседний сосуд под давлением p = F1/ω1 и действует на поверхность поршня площадью ω2 с силой, равной
Р2 = Р1 . ω 2/ ω 1, при этом
Р2/Р1 = ω 2/ ω 1.
Слайд 25
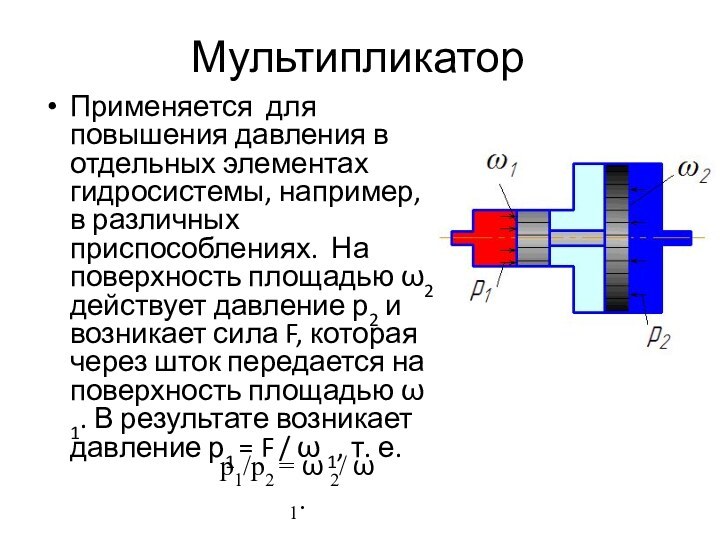
Мультипликатор
Применяется для повышения давления в отдельных элементах гидросистемы,
например, в различных приспособлениях. На поверхность площадью ω2 действует
давление р2 и возникает сила F, которая через шток передается на поверхность площадью ω 1. В результате возникает давление р1 = F / ω 1, т. е.р1/р2 = ω 2/ ω 1.
Слайд 26
Равновесие тел погруженных в жидкость
На тело, погруженное полностью
или частично в жидкость, действуют две силы:
Сила тяжести тела
G, приложенная в его центре тяжести С.Выталкивающая сила Р, приложенная в центре давления или, как называют еще, в центре водоизмещения D. Центром водоизмещения является центр тяжести вытесненного объема жидкости.
В зависимости от соотношения сил G и Р могут быть три состояния тела.
Если G больше Р, тело тонет.
Если G=Р, тело находится внутри жидкости в безразличном состоянии (тело плавает в погруженном состоянии).
Если G меньше Р, то тело всплывает до тех пор, пока сила тяжести вытесненной жидкости не станет равна силе тяжести тела G.
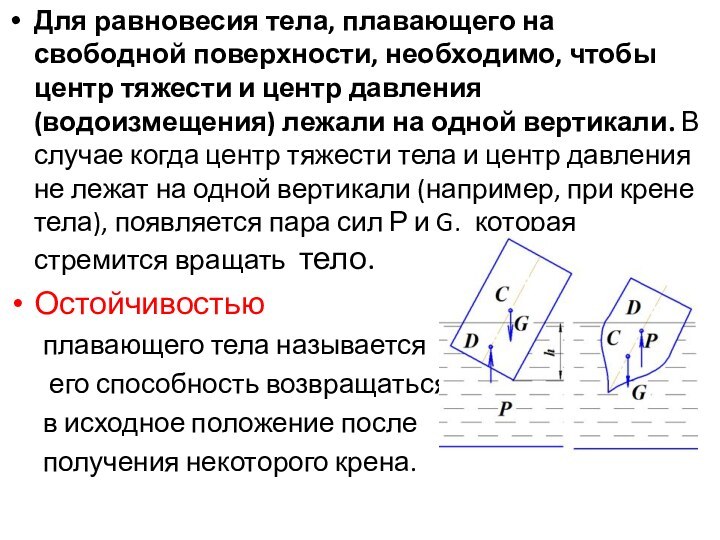
Слайд 27 Для равновесия тела, плавающего на свободной поверхности, необходимо,
чтобы центр тяжести и центр давления (водоизмещения) лежали на
одной вертикали. В случае когда центр тяжести тела и центр давления не лежат на одной вертикали (например, при крене тела), появляется пара сил Р и G, которая стремится вращать тело.Остойчивостью
плавающего тела называется
его способность возвращаться
в исходное положение после
получения некоторого крена.
Слайд 28
Задача
Кусок парафина объемом V находится между водой и
керосином. Какая часть объема парафина находится в воде, если
плотность керосина 0,8 т/м3, а парафина 0,9 т/м3?
Слайд 29
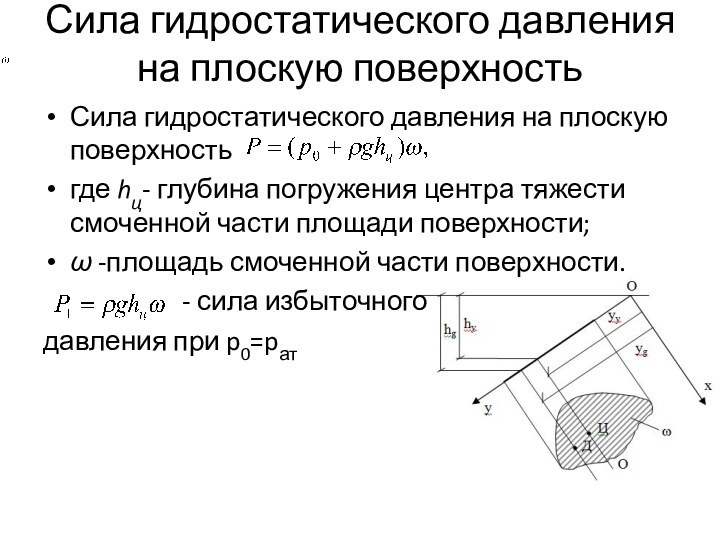
Сила гидростатического давления на плоскую поверхность
Сила гидростатического давления
на плоскую поверхность
где hц- глубина погружения центра тяжести смоченной
части площади поверхности;ω -площадь смоченной части поверхности.
- сила избыточного
давления при p0=pат
Слайд 30
Итак сила избыточного давления
Эта сила приложена в
центре давления, координата которого определяется по формуле
уц- координата центра
тяжести смоченной поверхности;
I0- момент инерции площади
смоченной части поверхности
относительно горизонтальной
оси, проходящей через центр ее тяжести.
Слайд 31
Сила гидростатического давления на криволинейную поверхность
Сила гидростатического давления
на криволинейную поверхность
где
- составляющие силы избыточного давления по соответствующим осям.В случае цилиндрической
поверхности
Рх и Рz- горизонтальная и
вертикальная
составляющие силы Р.
Слайд 32
Горизонтальная составляющая
Горизонтальная составляющая избыточного давления Рх равна
силе давления на вертикальную проекцию криволинейной поверхности
Рм -
манометрическое давление на поверхности жидкости;hц- глубина погружения центра тяжести вертикальной проекции криволинейной поверхности
ωz - площадь вертикальной
проекции.
Слайд 33
Вертикальная составляющая
Вертикальная составляющая Рz равна весу жидкости
в объеме тела давления V:
Тело давления расположено между вертикальными
плоскостями, проходящими через крайние образующие цилиндрической поверхности, самой цилиндрической поверхностью и свободной
поверхностью жидкости
или ее продолжением.