Слайд 2
Сущность формализованных методов прогнозирования
Эти методы базируются на математической
теории, которая
обеспечивает повышение достоверности и точности прогнозов,
значительно сокращает
сроки их выполнения,
позволяет обеспечить деятельность по обработке информации и оценке результатов.
Формализованные методы позволяют получать количественные показатели.
При разработке таких прогнозов исходят из предложения об инерционности системы.
Недостатком формализованных методов является ограниченная глубина упреждения, находящаяся в пределах эволюционного цикла развития системы, за пределами которого на надёжность прогнозов падает.
Слайд 3
Метод экстраполяция
это метод научного исследования, который основан
на распространении прошлых и настоящих тенденций, закономерностей, связей на
будущее развитие объекта прогнозирования.
Цель методов экстраполяции – показать, к какому состоянию в будущем может прийти объект, если его развитие будет осуществляться с той же скоростью или ускорением, что и в прошлом.
Слайд 4
Классификация формализованных методов прогнозирования
К методам экстраполяции относятся:
метод
скользящей средней
метод экспоненциального сглаживания
метод наименьших квадратов
Слайд 5
1.Сущность метода наименьших квадратов
Состоит в минимизации суммы
квадратических отклонений между наблюдаемыми и расчетными величинами, через уравнение
регрессии.
У t+1 = а*Х + b,
где t + 1 – прогнозный период;
Уt+1 – прогнозируемый показатель;
a и b - коэффициенты;
Х - условное обозначение времени.
Слайд 6
Недостатки метода наименьших квадратов:
прогноз будет точен для небольшого
периода времени и уравнение регрессии следует пересчитывать по мере
поступления новой информации;
сложность подбора уравнения регрессии, которая разрешима при использовании типовых компьютерных программ.
Слайд 7
2.Метод экспоненциального сглаживания
На среднесрочные прогнозы.
Только на
один период вперед.
Преимущества метода-он не требует обширной информационной
базы и предполагает её интенсивный анализ с точки зрения информационной ценности различных членов временной последовательности.
Слайд 8
Рабочая формула метода экспоненциального сглаживания:
где t – период,
предшествующий прогнозному;
t+1 – прогнозный период;
Ut+1 - прогнозируемый
показатель;
α - параметр сглаживания;
Уt - фактическое значение исследуемого показателя за период, предшествующий прогнозному;
Ut - экспоненциально взвешенная средняя для периода, предшествующего прогнозному.
Слайд 9
Затруднения:
выбор значения параметра сглаживания α;
определение начального значения Uo.
Примечание:
Чем
больше α, тем меньше сказывается влияние предшествующих лет.
-Если
значение α близко к единице, то это приводит к учету при прогнозе в основном влияния лишь последних наблюдений.
-Если значение α близко к нулю, то веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения.
Слайд 10
3. Метод скользящей средней
даёт возможность выравнивать динамический
ряд путём его расчленения на равные части с обязательным
совпадением в каждой из них сумм модельных и эмпирических значений.
Сглаживание с помощью скользящих средних основано на том, что в средних величинах взаимно поглощаются случайные отклонения.
-Периоды определения средней берутся одинаковыми.
-В расчетах участвуют все уровни ряда.
-Сглаженный ряд короче первоначального на (n–1) наблюдений, где n – величина интервала сглаживания.
Слайд 11
Рабочая формула:
где t + 1 – прогнозный период;
t – период, предшествующий прогнозному периоду (год, месяц и
т.д.);
Уt+1 – прогнозируемый показатель;
mt-1 – скользящая средняя за два периода до прогнозного;
n – число уровней, входящих в интервал сглаживания;
Уt – фактическое значение исследуемого явления за предшествующий период;
Уt-1 – фактическое значение исследуемого явления за два периода, предшествующих прогнозному
Слайд 12
виды моделей:
имитационные
и другие
оптимизационные
статические
комбинированные
Слайд 13
Оптимизационные расчёты осуществляются на основе разработанных экономикой математических
моделей и исходной информации с использованием специальных пакетов программ
и ЭВМ.
Имитационные модели, цель которых состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между её элементами.
Статистические методы. В тех случаях, когда анализ математической модели даже численными методами может оказаться нерезультативным из-за чрезмерной трудоемкости или неустойчивости алгоритмов в отношении погрешностей аппроксимации и округления, строится имитационная модель
Слайд 14
Комбинированное (аналитико-имитационное) моделирование позволяет объединить достоинства аналитического и
имитационного моделирования.
Такой подход позволяет охватить качественно новые классы систем,
которые не могут быть исследованы с использованием только аналитического или имитационного моделирования в отдельности.
Слайд 15
Задача. Имеются данные, характеризующие уровень безработицы в регионе,
%
Постройте прогноз уровня безработицы в регионе на ноябрь, декабрь,
январь месяцы, используя методы: скользящей средней
Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
Слайд 16
1. Определить величину интервала сглаживания, например равную 3
(n = 3).
2. Рассчитать скользящую среднюю для первых трех
периодов
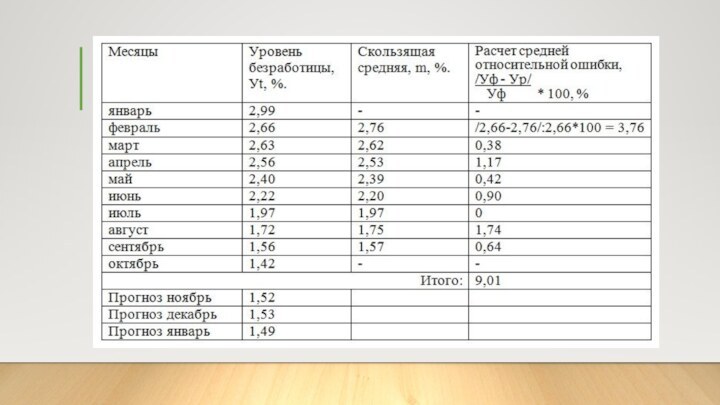
m фев = (Уянв + Уфев + У март)/ 3 = (2,99+2,66+2,63)/3 = 2,76
Далее рассчитываем m для следующих трех периодов февраль, март, апрель.
m март = (Уфев + Умарт + Уапр)/ 3 = (2,66+2,63+2,56)/3 = 2,62
Далее по аналогии рассчитываем m для каждых трех рядом стоящих периодов и результаты заносим в таблицу.
Решение :
Слайд 17
У ноябрь = 1,57 + 1/3 (1,42 –
1,56) = 1,57 – 0,05 = 1,52
Определяем скользящую среднюю
m для октября.
m = (1,56+1,42+1,52) /3 = 1,5
Строим прогноз на декабрь.
У декабрь = 1,5 + 1/3 (1,52 – 1,42) = 1,53
Определяем скользящую среднюю m для ноября.
m = (1,42+1,52+1,53) /3 = 1,49
Строим прогноз на январь.
У январь = 1,49 + 1/3 (1,53 – 1,52) = 1,49
Заносим полученный результат в таблицу.