- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Функции
Содержание
- 2. ПланОпределение функцииОбласть определения функцииМножество значенийСпособы задания функцииГрафик функции, определение и теоремыЧетность, нечетность функции7. Монотонные функции
- 3. Определение функцииПусть дано числовое множество Х и
- 4. Пусть дано некоторое множество Y и у
- 5. Если закон обозначен буквой f, то пишут
- 6. Множество значенийАргумент x є X, элемент y
- 7. Множество Е может совпадать с У, а
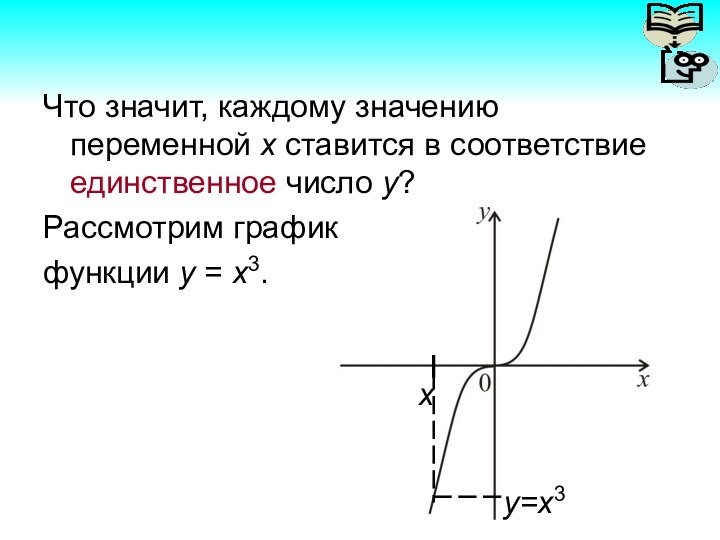
- 8. Что значит, каждому значению переменной х ставится в соответствие единственное число y?Рассмотрим графикфункции у = х3.у=х3
- 9. Обозначения и примерыx є X, где X
- 10. 2. Разность х – [x] называют дробной
- 11. Способы задания функцийТабличныйАналитический, т.е. при помощи формулы При помощи нескольких формулГрафический способСловесное задание функции
- 12. При помощи нескольких формулФункция Дирихле:
- 13. Словесное задание функцииПримеры1. f(n) равно n-му десятичному
- 14. Графический способ задания функцииОпределение графика функции.Графиком функции
- 15. Примеры и теоремаГрафиком у = х2 является
- 16. II. Обратно. Пусть множество G точек на
- 17. Пусть х є А. Сопоставим ему элемент
- 18. Окружность
- 19. Равенство функцийПусть функция f(х) определена на множестве
- 20. Сумма, разность, произве- дение и частное двух
- 21. Симметричное множествоОпределение. Числовое множество М называется симметричным
- 22. Четная функцияОпределение. Функция f(x) называется четной, если
- 23. Нечетная функцияОпределение. Функция f(x) называется нечетной, если
- 24. Бывают функции с несимметричной относительно нуля областью
- 25. Как определять четность/ нечетностьЕсли у функции область
- 26. Если f(− x) = f(x), то четная.Если
- 27. ПримерыОпределите, являются ли следующие функции четными или
- 28. График четной функцииТак как для четной функции
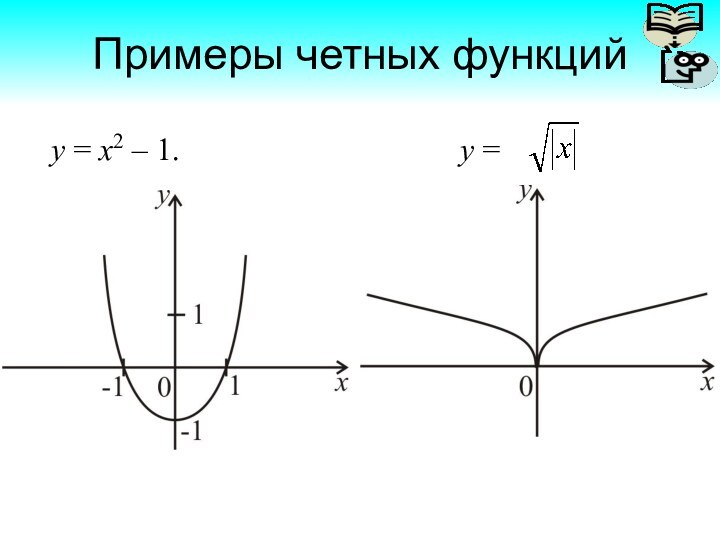
- 29. Примеры четных функций у = х2 –
- 30. График нечетной функцииПоскольку для нечетной функции справедливо
- 31. Точка А1 будет симметрична точке А(х0; у0)
- 32. Примеры нечетных функций y = х3
- 33. ТеоремаВсякая функция f(x) с областью опреде-ления, симметричной
- 34. g(x) = ½ (f(x) + f(− x))
- 35. Некоторые теоремы о четности (нечетности) Т.1. Сумма (разность)
- 36. Монотонные функции Строго монотонные функцииНазовем словом промежуток
- 37. Определение. Функция f(x) называется убывающей (строго убывающей)
- 38. Геометрически строго возрастающая функция изображается графиком, поднимающимся
- 39. Примеры монотонных функцийВозрастающие
- 40. Неубывающие и невозрастающие функцииОпределение. Функция f(x) называется
- 41. Определение. Функция f(x) называется невозрастающей на промежутке
- 42. Кусочно-монотонные функцииОдна и та же функция на
- 43. Определение. Функция f(x) на множестве Х называется
- 44. Докажем, что у = х2 возрастает на
- 45. Скачать презентацию
- 46. Похожие презентации
ПланОпределение функцииОбласть определения функцииМножество значенийСпособы задания функцииГрафик функции, определение и теоремыЧетность, нечетность функции7. Монотонные функции








![Функции 2. Разность х – [x] называют дробной частью числа х и обозначают](/img/tmb/13/1283511/43e6e14ba67416ec6c08c87988b88a4c-720x.jpg)


































Слайд 2
План
Определение функции
Область определения функции
Множество значений
Способы задания функции
График функции,
определение и теоремы
Слайд 3
Определение функции
Пусть дано числовое множество Х и его
элемент х є X, который назовем переменной величиной.
Множество
X всех значений, которые мо-жет принимать данная переменная величина x, называется областью изме-нения данной переменной величины x.
Переменные величины принято обозна-
чать маленькими латинскими буквами, расположенными в конце алфавита.
Слайд 4 Пусть дано некоторое множество Y и у –
его элемент.
Если каждому значению переменной x из множества
X ставится в соответствие по известному закону (или правилу) некоторое число y, единственное для каждого x, то говорят, что на множестве Х задана функция y = y(x). К примеру, в качестве правила можем взять возведение в квадрат переменной х.
Слайд 5
Если закон обозначен буквой f, то пишут
y
= f(x).
При этом переменная х называется аргументом функции
или независимой переменной, множество Х – областью определения (областью задания) функции.
Слайд 6
Множество значений
Аргумент x є X, элемент y принадлежит
Y и должен определяться однозначно.
Число у, соответствующее данному
значению х, называется частным значением функции в точке х. Совокупность всех частных значений образует вполне определенное множество, которое называют областью значений или множеством значений функции и обозначают Е(у). Слайд 7 Множество Е может совпадать с У, а может
и не совпадать. Например,
пусть Х = R и Y
= R. Пусть функция есть возведение в квадрат, т. е. y = x2. Тогда множество значений – все неотрицательные числа
E(y)= [0; +∞).
Слайд 8 Что значит, каждому значению переменной х ставится в
соответствие единственное число y?
Рассмотрим график
функции у = х3.
у=х3
Слайд 9
Обозначения и примеры
x є X, где X =
D(f) = Def(f).
y є Y, где Y = E(f)
= E(y). Примеры функций
1. Целой частью числа х (обозначается [x] и читается антье от х) называется наибольшее целое число, не превосходящее х:
f(x)= [x]. Def(f) = R; E(f) = Z.
Слайд 10 2. Разность х – [x] называют дробной частью
числа х и обозначают f(x)= {x}. Def(f) = R;
E(f) = [0; 1).3. f(n) = 1 + 2 + 3 + … + n.
4. y = sin x.
5. y = 6.
Слайд 11
Способы задания функций
Табличный
Аналитический, т.е. при помощи формулы
При
помощи нескольких формул
Графический способ
Словесное задание функции
Слайд 12
При помощи нескольких
формул
Функция Дирихле:
у =
1, если х – рациональное число,
у = 0, если х – иррациональное число.х2, если | x | 1;
у =
| x | + 2, если | x | > 1.
Слайд 13
Словесное задание функции
Примеры
1. f(n) равно n-му десятичному знаку
в разложении в бесконечную десятичную
дробь= 1,4142…; f(1) = 4; f(2) = 1; f(3) = 4;
2. f(x) = [x] (антье от х) – наибольшее целое число, не превосходящее данного действительного числа х.
Слайд 14
Графический способ
задания функции
Определение графика функции.
Графиком функции y =
f(x), где x є Def(y), называется множество точек координатной
плоскости ХОУ, абсциссы которых принадлежат области определения, а ординаты равны соответствующим значениям функции:x є Def(y), y = f(x). Множество точек плоскости ( x; f(x)) = (x; y) есть график.
Слайд 15
Примеры и теорема
Графиком у = х2 является парабола,
а графиком функции у = kx + b –
прямая.Основное свойство графика (теорема)
Всякая вертикальная прямая пересекает график не более чем в одной точке.
Док-во. I. Пусть дан график y = f(x).
Если для какой-то точки х0 найдутся две
различные точки графика, то будем иметь
y1 = f(x0) ≠ y2 = f(x0), что невозможно по
определению функции.
Слайд 16 II. Обратно. Пусть множество G точек на плоскости
таково, что каждая вертикальная прямая пересекает его не более
чем в одной точке. Докажем, что множество G является графиком некоторой функции.Спроектируем множество G на ось абсцисс и обозначим проекцию через А. Назовем А областью определения функции.
Слайд 17
Пусть х є А.
Сопоставим ему элемент у
следующим образом:
проведем вертикальную прямую через точку (х; 0).
Она пересечет множество G в одной точке, ординату которой назовем у. Получили закон x → y. Это число у удовлетворяет определению функции.
Слайд 18
Окружность
x2 + y2 = r2 ;
y2 = r2 – x2;
y = ± ;
y1 = + ; y2 = − .
Здесь два графика: верхняя полуокружность у1 и нижняя полуокружность у2.
Слайд 19
Равенство функций
Пусть функция f(х) определена на множестве Х1,
а функция g(х) – на множестве Х2. Предположим, что
пересечение множеств Х1 и Х2 не пусто, т.е. Х = Х1 ∩ Х2 ≠ Ø.Определение. Функции f (x) и g(x) называются равными на множестве X, если для всякого x є X равны их значения, т.е.
x є X ( f(x) = g(x) ).
Слайд 20
Сумма, разность, произве-
дение и частное двух функций
Суммой функций
f (x) и g(x) на множестве Х называется функция
h(x), которая для каждого x є X принимает значение, равное сумме значений функций f (x) и g(x) , т.е. x є X ( h(x) = f(x) + g(x) ).Аналогично определяется разность, произведение и частное двух функций, при этом для частного оговаривается условие, что функция, стоящая в знаменателе, не равна нулю.
Слайд 21
Симметричное множество
Определение. Числовое множество М называется симметричным относительно
начала координат, если для любого действительного числа
а
М число −а также принадлежит множеству М.а М => − а М.
Примеры. [ −1; 1],
(−∞; 0) U (0; +∞), (−5; −2] U [2; 5).
Слайд 22
Четная функция
Определение. Функция f(x) называется четной, если
1)
ее область определения симметрична относительно нуля, и
2) имеет
место равенство f(− x) = f(x). Другое опр-ние. Функция f(x), заданная
на множестве Х, называется четной, если для любого числа х є D(f) число − х также принадлежит D(f) и имеет место равенство f(− x) = f(x).
Слайд 23
Нечетная функция
Определение. Функция f(x) называется нечетной, если
1) ее область определения симметрична относительно нуля, и
2)
имеет место равенство f(− x) = − f(x). Другое опр-ние. Функция f(x), заданная на множестве Х, называется нечетной, если для любого числа х є D(f) число − х также принадлежит D(f) и имеет место равенство
f(− x) = − f(x).
Слайд 24
Бывают функции с несимметричной относительно нуля областью определения.
Например.
Определите, является ли функция у =
четной или нечетной.Решение. О.о. есть [0; +∞) – несимметричное множество. Не является. Или говорят, что четность не определяется.
Слайд 25
Как определять четность/
нечетность
Если у функции область определения симметрична
относительно нуля, то проверяем равенства f(− x) = f(x)
или f(− x) = − f(x). Для этого в формулу для у подставим вместо х число −х.Итак, чтобы определить четность (нечетность) функции, необходимо
проверить на симметричность ее О.О.;
вычислить f(− x).
Слайд 26
Если f(− x) = f(x), то четная.
Если
f(− x) = − f(x), то нечетная.
Определите, являются ли
следующие функции четными или нечетными.1) у = х2 ;
у = │х │;
у = х3;
у = sin2x;
Слайд 27
Примеры
Определите, являются ли следующие функции четными или нечетными.
5)
у = х2 + 1 ;
6) у
= х3(х – 1);7) у = х2 – х3 ;
8) у = 2(х2 – х);
9) у = 3х3 + х5;
10) у = х ∙│х │.
Слайд 28
График четной функции
Так как для четной функции выполнено
равенство f(− x) = f(x), то ее график симметричен
относительно оси Оу. Это значит, что та часть графика, которая расположена в правой полуплоскости, отображена зеркально относительно оси Оу в левую полуплоскость.
Слайд 30
График нечетной функции
Поскольку для нечетной функции справедливо равенство
f(− x) = − f(x), то ее график симметричен
относительно начала координат.Две точки на координатной плоскости называются симметричными относительно начала координат, если начало координат является серединой отрезка, соединяющего эти две точки.
Слайд 31
Точка А1 будет симметрична точке
А(х0; у0) относительно
начала координат, если она имеет координаты А1(− х0; −
у0).Найдите точку, симметричную точке
( -5; 2);
(0; 3);
( -4; 0);
( 1; 1).
Слайд 33
Теорема
Всякая функция f(x) с областью опреде-ления, симметричной относительно
начала координат, может быть пред-ставлена в виде суммы четной
и нечетной функций.Док-во. Составим две вспомогательные функции g(x) и h(x).
Слайд 34 g(x) = ½ (f(x) + f(− x)) ;
h(x) = ½ (f(x) − f(−
x)).Функция g(x) – четная.
Функция h(x) – нечетная.
Сложим g(x) + h(x), получим f(x).
Теорема доказана.
Слайд 35
Некоторые теоремы
о четности (нечетности)
Т.1. Сумма (разность) двух четных
функций есть функция четная.
Т2. Произведение (частное) двух четных функций
также является четной функцией.Т3. Сумма (разность) двух нечетных функций является также нечетной функцией.
Т4. Произведение (частное) двух нечетных функций есть функция четная.
Слайд 36
Монотонные функции
Строго монотонные функции
Назовем словом промежуток любой интервал,
отрезок, полуинтервал, бесконечный полуинтервал и обозначим его < a;
b>. Пусть на промежутке < a; b> задана функция y = f(x).Определение. Функция f(x) называется возрастающей (строго возрастающей) на промежутке < a; b>, если для любых значений x1, ,x2 из этого промежутка при
x1 < x2 выполняется неравенство
f(x1) < f(x2).
Слайд 37 Определение. Функция f(x) называется убывающей (строго убывающей) на
промежутке < a; b>, если для любых значений x1,
,x2 из этого промежутка при x1 < x2 выполняется неравенствоf(x1) > f(x2).
Слайд 38 Геометрически строго возрастающая функция изображается графиком, поднимающимся вверх
вправо, а строго убывающая – графиком, опускающимся вниз вправо.
Строго возрастающие и убывающие функции называются монотонными.
Слайд 39
Примеры монотонных функций
Возрастающие
Убывающие
y =
x2 на [0; +∞); y = x2 на (−∞; 0];y = x3; y = − на [0; +∞);
y = на [0; +∞); y = 1 / x .
Слайд 40
Неубывающие и
невозрастающие функции
Определение. Функция f(x) называется неубывающей на
промежутке < a; b>, если для любых значений x1,
,x2 из этого промежутка при x1 < x2 выполняется неравенство f(x1) ≤ f(x2).
Слайд 41
Определение. Функция f(x) называется невозрастающей на промежутке
a; b>, если для любых значений x1, ,x2 из
этого промежутка при x1 < x2 выполняется неравенство f(x1) ≥ f(x2).Функции невозрастающие и неубывающие также называются монотонными.
Слайд 42
Кусочно-монотонные функции
Одна и та же функция на различных
промежутках может вести себя по-разному. Так, функция у =
х2 строго убывает на (−∞; 0] и строго возрастает на [0; +∞).Подобные функции называются кусочно-монотонными.
Слайд 43 Определение. Функция f(x) на множестве Х называется кусочно-монотонной,
если Х есть объединение конечного числа промежутков, на каждом
из которых f(x) монотонна.Слайд 44 Докажем, что у = х2 возрастает на [0;
+∞).
Пусть х1 < х2 и оба числа неотрицательны.
f(x2)
– f(x1) = x22 – x12 = (x2 – x1) (x2 + x1).Так как х1 < х2 , то (x2 – x1) > 0.
Так как х1 ≥ 0 и х2 ≥ 0 , то сумма x2 + x1 ≥ 0.
Сл-но, произведение тоже ≥ 0.
Таким образом, доказали, что у = х2 возрастает на [0; +∞).





























