- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Классная работаГеометрия
Содержание
- 2. Определение параллельных прямых Две прямые на
- 3. Определение секущей прямой Прямая c называется
- 4. Теорема. Если при пересечении двух прямых секущей накрест
- 5. Если при пересечении двух прямых секущей накрест
- 6. Если при пересечении двух прямых секущей соответственные
- 7. Если при пересечении двух прямых секущей сумма
- 8. Решение задач №1. На рисунке
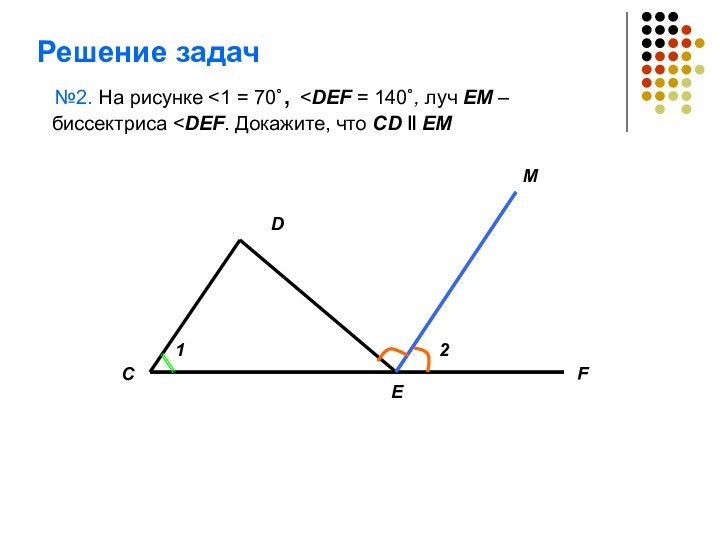
- 9. Решение задач №2. На рисунке
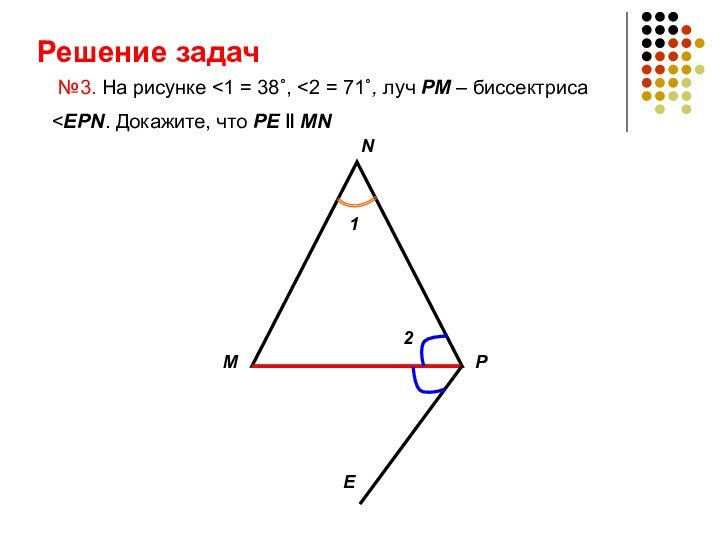
- 10. Решение задач №3. На рисунке
- 11. Домашнее заданиеВыучить 3 теоремы с доказательствами.По учебнику № 186, 187, 188
- 12. Скачать презентацию
- 13. Похожие презентации





Слайд 2
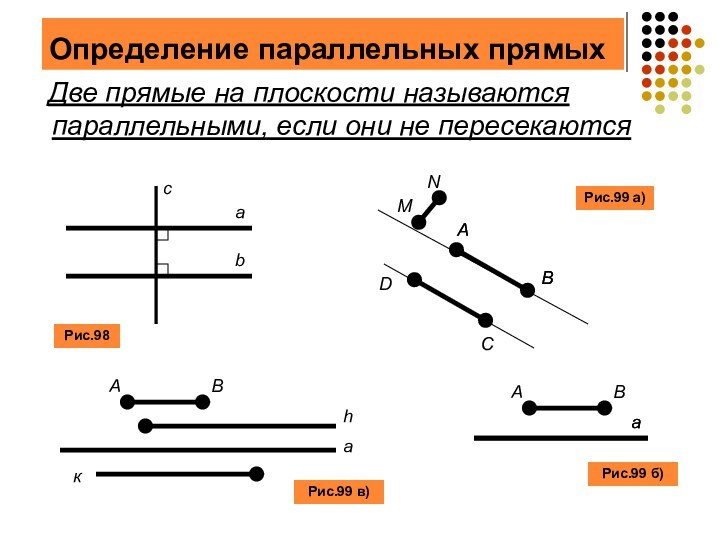
Определение параллельных прямых
Две прямые на плоскости
называются параллельными, если они не пересекаются
Слайд 3
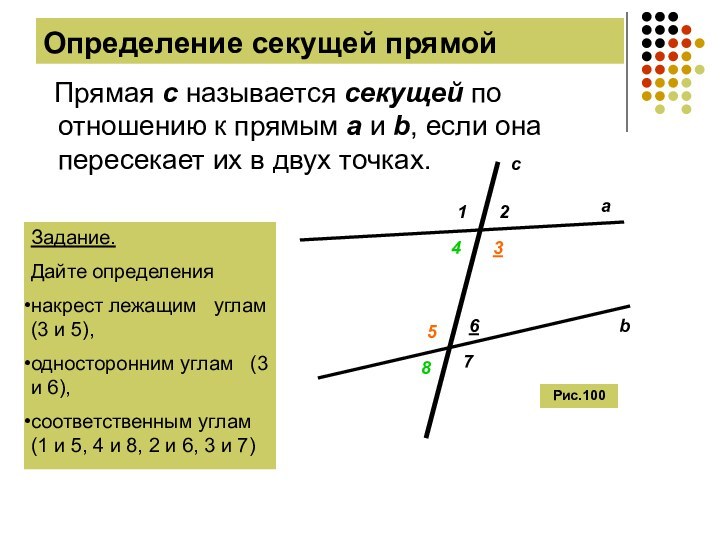
Определение секущей прямой
Прямая c называется секущей
по отношению к прямым а и b, если она
пересекает их в двух точках.a
b
с
Рис.100
1
2
4
3
5
6
8
7
Задание.
Дайте определения
накрест лежащим углам (3 и 5),
односторонним углам (3 и 6),
соответственным углам (1 и 5, 4 и 8, 2 и 6, 3 и 7)
Слайд 4
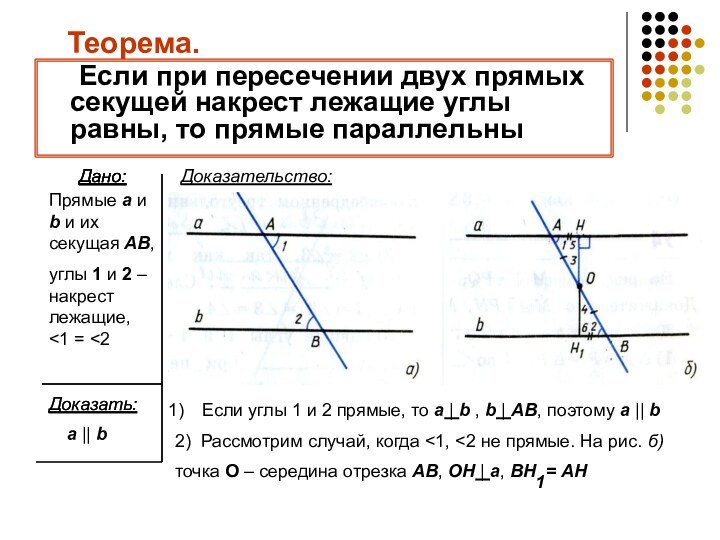
Теорема.
Если при пересечении двух прямых секущей накрест лежащие
углы равны, то прямые параллельны
Дано:
Прямые a и b и
их секущая AB,углы 1 и 2 – накрест лежащие, <1 = <2
Доказать:
a || b
Доказательство:
Если углы 1 и 2 прямые, то a | b , b | AB, поэтому a || b
2) Рассмотрим случай, когда <1, <2 не прямые. На рис. б)
точка О – середина отрезка AB, OH | a, BH = AH
1
Дано:
Доказать:
Дано:
Слайд 5 Если при пересечении двух прямых секущей накрест лежащие
углы равны, то прямые параллельны
3) ∆OHA= ∆ OH B
по _____________________________________, поэтому <3 = <4 и <5 = <64) Из равенства углов 3 и 4 следует, что точка H лежит на продолжении луча OH, т.е. точки H, O и H лежат _______________
3) Из равенства углов 5 и 6 следует, что <6 =_____, т.е. HH _____b
4) Итак, прямые a и b ________ к прямой ____, поэтому они __________________. Теорема доказана
1
1
1
1
Слайд 6 Если при пересечении двух прямых секущей соответственные углы
равны, то прямые параллельны
Теорема.
Доказать:
Дано:
Прямые a и b и их
секущая AB,углы 1 и 2 – соответственные,
<1 = <2
a || b
Доказательство:
1) <1 = <2 по ____________________,
<2 = <3 , т.к. эти углы ____________, следовательно, <1 = <3
2) Равные углы 1 и 3 - __________________________________________, поэтому a || b. Теорема доказана.
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны
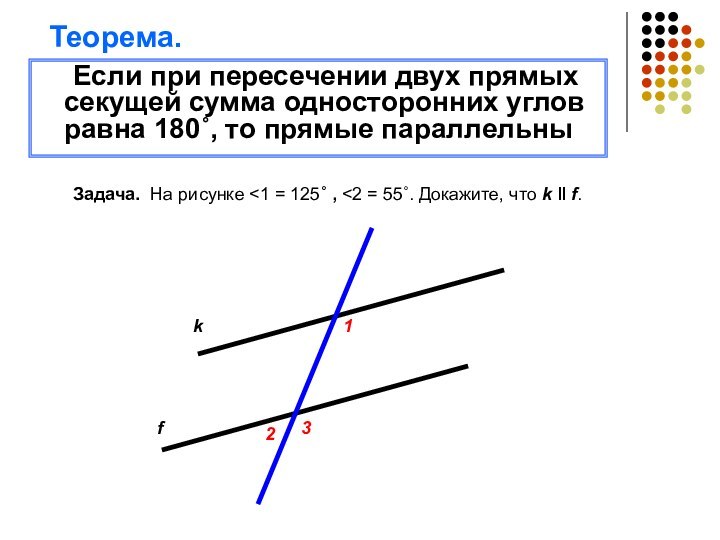
Слайд 7 Если при пересечении двух прямых секущей сумма односторонних
углов равна 180˚, то прямые параллельны
Теорема.
Задача. На рисунке
= 125˚ , <2 = 55˚. Докажите, что k ‖ f. k
f
1
3
2
Слайд 8
Решение задач
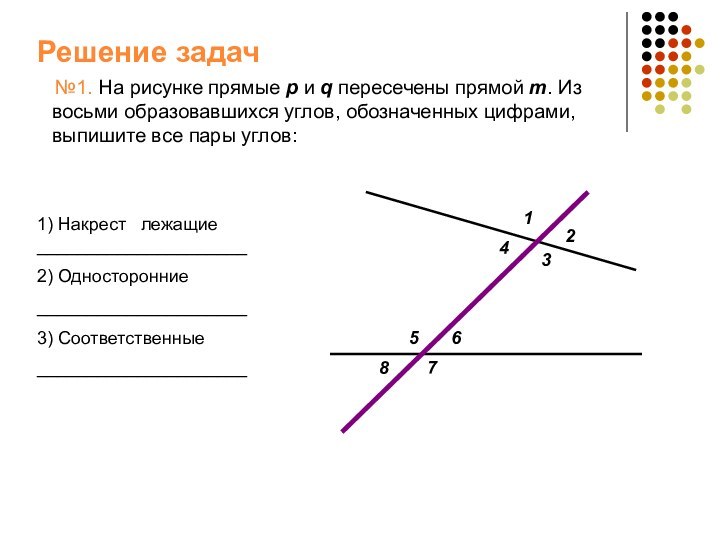
№1. На рисунке прямые
p и q пересечены прямой m. Из восьми образовавшихся
углов, обозначенных цифрами, выпишите все пары углов:1) Накрест лежащие _____________________
2) Односторонние
_____________________
3) Соответственные
_____________________
1
2
4
3
5
6
7
8





























