Презентация на тему Крива лінія як геометричне місце точок.

в даній точці кривої, називається нормальною площиною; всі нормалі

для даної точки лежать в нормальній площині.

Нормаль, що лежить в дотичній площині, називають головною нормаллю, а нормаль, перпендикулярна дотичній площині, називається бінормаль. Також нормаллю і бінормаль для стислості можуть називати одиничні вектори вздовж цих прямих.

функція з порядком гладкості r має неперервну похідну порядку

r. Множина таких функцій, визначених у області позначається.
означає, що для будь-якого r, а
означає, що f — аналітична.
Якщо порядок гладкості не вказаний, то звичайно припускають його достатнім для того, щоб мали сенс всі дії, що виконуються над функцією по ходу поточного міркування.

 
Гла́дка функція або неперервно-диференційовна функція — це функція, що має неперервну похідну на всій області визначення.

Гладка крива - в кожній точці є дотична, причому при русі вздовж кривої кут нахилу дотичній змінюється безперервно.

описують відхилення того або іншого геометричного «об'єкта» (кривої, поверхні,

риманова простору тощо) від відповідних «плоских» об'єктів (пряма, площина, евклідів простір тощо).

Зазвичай кривина визначається для кожної точки на «об'єкті» і виражається як значення деякого диференціального виразу 2-го порядку. Іноді кривина визначається в інтегральному смислі, наприклад як міра, такі визначення використовують для «об'єктів» зниженої гладкості. Як правило, тотожне перетворення на нуль кривини в усіх точках означає збіг (локальний, але не глобальний) «об'єкта», що вивчається, з «плоским» об'єктом.

,називається дотичною до кола. Спільна точка називається точкою дотику.
Таке означення дотичної не

може бути перенесено на всі криві (парабола, синусоїда, гіпербола тощо).

Величина, обернена до кривини кривої, називається радіусом кривини; він збігається з радіусом дотичного кола в даній точці кривої. Центр цього кола називається центром кривини.

По відношенню до своєї еволюти будь крива є евольвентою.
Якщо

лінії задані параметричними рівняннями
то еволюта має рівняння:

Синім кольором показана гіпербола. Зеленим кольором - еволюта правої гілки цієї гіперболи. Червоним кольором показане коло, відповідної кривизни гіперболи в її вершині.

центрів кривизни плоскої кривої l називається еволюти цієї кривої

; крива l по відношенню до своєї еволюти називається евольвентою. Евольвента l кривої m може бути отримана як траєкторія кінця У нитки AB , яка намотується на лінію m або розмотується з неї (цим побудовою евольвенти і пояснюється ін її назв.. Зазначене побудова евольвенти робить ясним наступні властивості Е. і е. . : 1) дотична CD в довільній точці С еволюти є нормаллю у відповідній точці D евольвенти ( отже , евольвента є ортогональна

траєкторія дотичних еволюти ), 2) всяка ортогональна траєкторія дотичних кривої т є евольвентою (тому у даної кривої нескінченно багато евольвент ) ; 3 ) різницю радіусів кривизни AB і CD в точках в і D евольвенти дорівнює довжині дуги AC еволюти ; 4 ) Еволюта є обвідної сімейства нормалей евольвенти .

або незамкнута), утворена сполученням дуг: окружностей. Існує декілька різновидів

коробових кривих.
Овал - замкнена коробова крива, що має дві осі симетрії. Елементами, що визначають розмір овалу, є його довжина і ширина, вимірювані по осях симетрії.

Побудова овалу по його довжині AB і ширині CD показано на малюнку. Спочатку проводять дві взаємно перпендикулярні прямі, що перетинаються в точці О (а). На горизонтальній прямій в обидві сторони від точки О відкладають відрізок АВ/2, а на вертикальній CD/2. Точки A і С з'єднують прямою лінією і з точки О описують дугу радіусом OA до перетину її з прямою CD в точці E.

На прямій AC відкладають відрізок CF = CE і отримують точку F. Через середину відрізка AF проводять перпендикуляр і на перетині його з прямими AB і CD отримують точки O1 і O2. На прямих AB і CD будують точки O3 і O4, симетричні точкам O1 і O2 щодо центру О (рис. б). Точки O1, O2, O3, O4 є центрами сполучених дуг, що визначають контур овалу, а точки дотику дуг розташовуються на прямих O1O2, O3O2, O1O4 і O3O4. З центрів O1 і O3 описують дуги радіусом R1 = O1A, а з центрів O2 і O4 - дуги радіусом R2 = O2C і отримують контур овалу.

нормалях на рівні відрізки, називаються еквідистантними, або рівновіддаленими. Такі

криві зазвичай будують за допомогою циркуля, проводячи ряд дуг на заданій відстані (рис. 1, а), для чого центри дуг розташовують на заданій кривій а; до побудованим дугам проводять обвідну їх еквідистантну криву а'. У ряді випадків еквідистантні криві значно відрізняються за своєю формою від заданої кривої.

Так, еквідистантна крива b '(рис. 1, б), проведена зовні еліпса b, вже не є еліпсом, а крива b", проведена усередині еліпса b, полягає, крім того, з чотирьох ділянок, розмежованих крапками повернення В.

Сукупність усіх еквідистантних точок називається еквідістантною кривою. Розрізняють зовнішню і внутрішню еквідістанти (для замкнутих кривих) або праву і ліву (при введеному напрямку кривої) для незамкненою кривої.

довжина нормалі, яка будується для кожної точки вихідної кривої,

є сталою – величина вектора a. Якщо ця довжина змінюється при переміщенні точки по кривій, наприклад, в залежності від відстані до кривої, одержаної на попередньому кроці – називатимемо криву, що буде побудована, квазіеквідистантною кривою ІІ-го виду

Для побудови квазіеквідистантних кривих застосовано два підходи. Перший заснований на дискретному представленні кривих – в кожній точці вихідної кривої будується нормаль, попередньо визначивши її довжину в залежності від заданих умов, та додається заданий вектор зсуву. Далі за одержаними точками визначається крива. Другий підхід базується на здобутті аналітичного виразу для кривої за рівнянням вихідної кривої, залежністю зміни довжини нормалі та вектору зсуву.

є реґулярними. 
Під цією назвою об'єднуються точки різного типу:
-вузлові точки —

в яких крива сама себе перетинає;
-ізольовані точки — розташовані окремо від кривої, проте з координатами, які задовольняють рівнянню кривої;
-точки повернення або загострення — в яких напрям кривої змінюється на обернений; розрізняють точки повернення : 1-го роду і 2-го роду, в залежностівід розташуваннядотичної стосовно обох віток;
-точки самодотикання — в яких крива сама до себе дотикається;
-точки зламу — в яких крива "стрибком" змінює свій напрям причому на відміну від точки повернення дотичні до обох частин кривої в точці зламу різні;
-точки закінчення — на яких крива обрвається;
-асимптотичні точки — точки, до яких крива наближаюється на завгодно малу відстань.
-точки перегину - точки кривої, в яких змінюється знак кривизни.

від площин проекцій на максимальну або мінімальну відстань (у

найближчій околиці - справа і зліва).

Класифікація точок розриву функції
Всі точки розриву функції поділяються на точки розриву першого і другого роду . Кажуть , що функція f ( x ) має точку розриву першого роду при x = a , якщо в цей точці Існують лівобічний межа і правобічний межа ;
Ці односторонні межі кінцеві. При цьому можливе наступні два випадки : Лівобічний межа і правобічний межа рівні один одному :
Така точка називається точкою усувного розриву . Лівобічний межа і правобічний межа не рівні один одному : Така точка називається точкою кінцевого розриву . Модуль різниці значень односторонніх меж називається стрибком функції .
Функція f ( x ) має точку розриву другого роду при x = a , якщо принаймні один з односторонніх меж не існує або дорівнює нескінченності .

кривої змінюється на обернений; розрізняють точки повернення : 1-го

роду і 2-го роду, в залежностівід розташування дотичної стосовно обох гілок;
Точка повернення 1-го роду (а) — різні гілки кривої розташовані по різні сторони від загальної дотичної і утворюють вістря, як в
кривої в2 — х 3 = 0
Точка повернення 2-го роду (б) — різні гілки кривої розташовані по одну сторону від загальної дотичної, як в кривої  ( в — x 2 ) 2 — х 5 = 0

опуклу частину від вгнутої.
Дослідження функції не обходиться без встановлення

інтервалів опуклості та вгнутості, причому їх можуть розділяти як точки перегину, так і критичні точки ІІ роду.

Крива називається опуклою на інтервалі , якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.

Крива називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.

На рисунку вище крива опукла на інтервалі ( а,b)
 та вгнута на  (b,c) в точці  x=b, функція має перегин. 

= 0 особлива точка, до якої звертаються в нуль

часні похідні до порядку включно і не дорівнює нулю хоча б одна з приватних похідних (n +1)-го порядку.

Точка зламу або кутова точка - особлива точка кривої, що володіє тими властивістями, що й гілки кривої, на які ця точка ділить вихідну криву, має у цій точці різні (односторонні) дотичні.

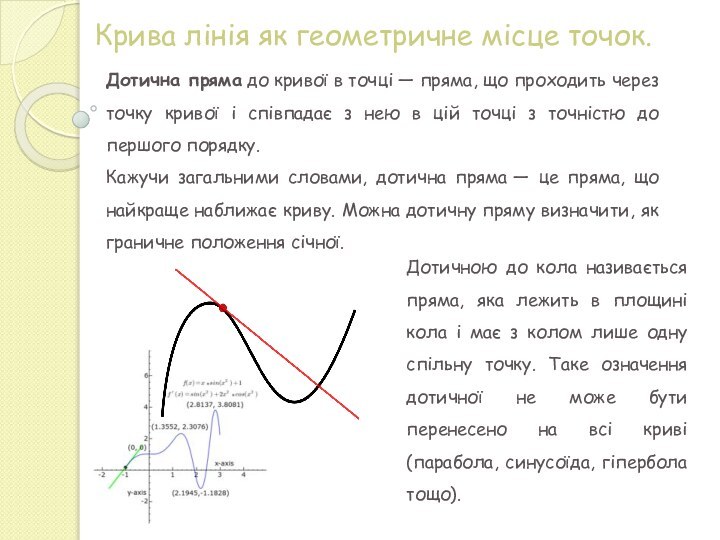
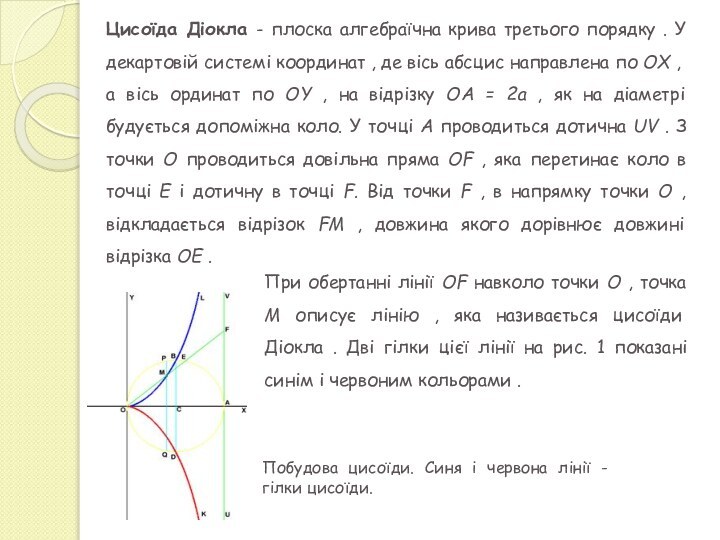
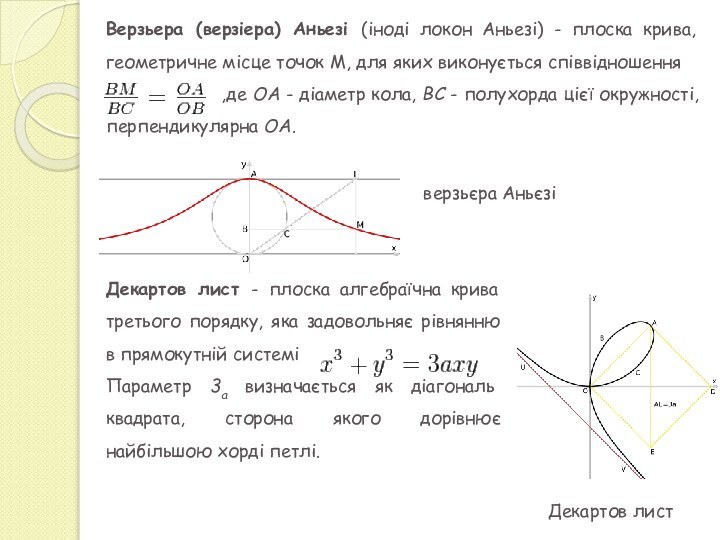
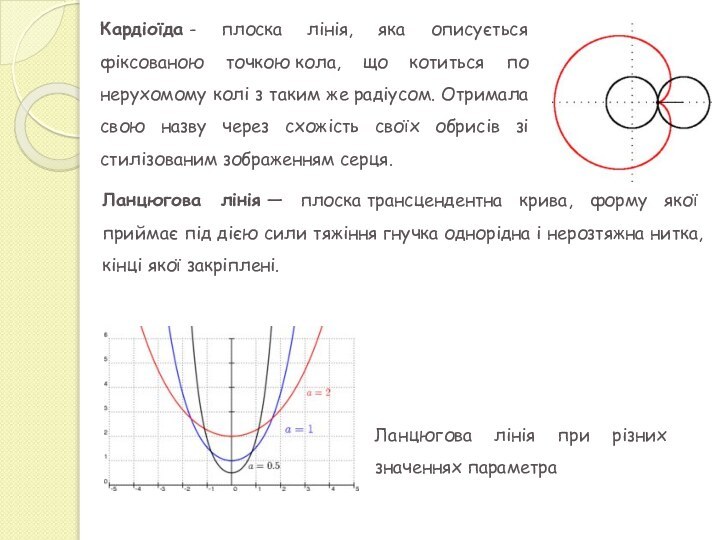
конуса площиною, що не проходить через його вершину.
можуть бути

трьох типів:
січна плоскість пересікає всі створюючі конуса в точках одного нього полості ; лінія пересічення є замкнута овальна крива — еліпс ; коло як окремий випадок еліпса виходить, коли січна плоскість перпендикулярна осі конуса.
Січна плоскість паралельна одній з дотичної плоскості конуса; у перетині виходить незамкнута, вирушаюча в нескінченність крива — парабола, цілком лежача на одній порожнині.

3) Січна плоскість пересікає обидві порожнини конуса; лінія пересічення — гіпербола — складається з двох однакових незамкнутих, таких, що тягнуться в нескінченність частин (гілок гіперболи), лежачих на обох порожнинах конуса.

К. п. були відомі вже математикам Древньої Греції (наприклад, Менехму, 4в. до н.е.(наша ера)); за допомогою цих кривих вирішувалися деякі завдання на побудову (подвоєння куба і ін.), що виявилися недоступними при використанні простих креслярських інструментів, — циркуля і лінійки. В дослідженнях, що дійшли до нас, грецькі геометри отримували К. п., проводячи січну площину перпендикулярно до однієї із створюючих, при цьому, залежно від кута при вершині конуса (тобто найбільшого кута між створюючими одній порожнині), лінія перетину виявлялася еліпсом якщо цей кут —гострий, параболою, якщо — прямою, і гіперболою, якщо — тупий. Найповнішим спогадом, присвяченим цим кривим, були «Конічні перетини» Аполонія Пергського (близько 200 до н.е.(наша ера)). Подальші успіхи теорії До. с. пов'язані із створенням в 17 ст нових геометричних методів: проективного (французькі математики Ж. Дезарг, Би. Паськаль) і особливо координатного (французькі математики Р. Декарт, П. Ферма).

центр симетрії (центр), тобто є еліпсом або гіперболою, його

рівняння може бути приведене (шляхом перенесення початку координат в центр) до вигляду:

a 11 x 2 +2a 12 xy + a 22 y 2 = a 33 .

Подальші дослідження таких (званих центральними) До. с. показують, що їх рівняння можуть бути приведені до ще простішому вигляду:

Ах 2 + Ву 2 = З,              (1)

якщо за напрями осей координат вибрати т.з. головні напрями — напрями головних осей (осей симетрії) До. с. Якщо А і В мають однакові знаки (співпадаючі із знаком З), то рівняння (1) визначає еліпс; якщо А і В різного знаку, то — гіперболу.
Рівняння параболи привести до вигляду (1) не можна. При належному виборі осей координат (одна вісь координат — єдина вісь симетрії параболи, інша — перпендикулярна до неї пряма, що проходить через вершину параболи) її рівняння можна привести до вигляду:

y 2 = 2рх.

прямокутні координати яких задовольняють рівняння виду

в якому принаймні один

з коефіцієнтів
відмінний від нуля.

Класифікація кривих другого порядку
Крива другого порядку називається невиродженої, якщо

Вироджені криві
Крива другого порядку називається виродженою, якщо

Лекальними називаються такі криві, точки яких не лежать
на колі та які креслять за допомогою лекал.

Циклоїда— плоска трансцендентна крива. Циклоїда визначається кінематично як траєкторія фіксованої точки кола радіуса r, що котиться без ковзання по прямій.

по зовнішній стороні іншого кола без проковзування.
Гіпоцикло́їда  — плоска крива,

що утворюється точкою кола, що котиться по внутрішній стороні іншого кола без проковзування.

Евольвента плоскої лінії L — це лінія L*, по відношенню до якої L є еволютою. Іншими словами, це крива, що описується кінцем гнучкої нерозтяжної нитки закріпленої в деякій точці, що змотується з плоскої кривої.

Евольвента кола

від зміни центрального кута, називається синусоїдою.
Синусоїда — плоска крива,

що задається рівнянням

Спіраль Архімеда — крива, яку описує точка M під час її рівномірного руху зі швидкістю v уздовж прямої, що рівномірно обертається в площині навколо однієї зі своїх точок О із кутовою швидкістю ω. Спіраль названо ім'ям Архімеда, який вивчив її властивості.

Якщо в початковий момент руху точки М і О збігаються, а полярна вісь збігається з початковим розташуванням рухомої прямої, то рівняння спіралі Архімеда у полярних координатах має вигляд ρ = аω.

Три повороти на 360°

спіралі, що часто зустрічається в природі.
Логарифмічна спіраль була

вперше описана Декартом і пізніше інтенсивно досліджена Бернуллі, який називав її Spira mirabilis —

«дивовижна спіраль». Власне термін «логарифмічна спіраль» першим вжив П'єр Варіньон

Логарифмічна спіраль (нахил 10°)

Конхоїда кривої— пласка крива, що виходить при збільшенні або зменшенні радіус-вектора кожної точки даної пласкої кривої на постійну величину.

Інакше, конхоїда пласкої кривої L відносно точки О – пласка крива, що описується кінцями відтинка, середина якого рухається по кривій L, а продовження відтинка проходить через фіксовану точку площини О.

. У декартовій системі координат , де вісь абсцис

направлена ​​по OX , а вісь ординат по OY , на відрізку OA = 2a , як на діаметрі будується допоміжна коло. У точці A проводиться дотична UV . З точки O проводиться довільна пряма OF , яка перетинає коло в точці E і дотичну в точці F. Від точки F , в напрямку точки O , відкладається відрізок FM , довжина якого дорівнює довжині відрізка OE .

При обертанні лінії OF навколо точки O , точка M описує лінію , яка називається цисоїди Діокла . Дві гілки цієї лінії на рис. 1 показані синім і червоним кольорами .

Побудова цисоїди. Синя і червона лінії - гілки цисоїди.

від яких до двох заданих точок (фокусів) незмінна і

дорівнює квадрату половини відстані між фокусами.

Лемніската —крива четвертого порядку.

Вона має дві осі симметрії: пряма, на якій лежить F1 F2, і серединний перпендикуляр цього відрізка, в простішому (даному) випадку — вісь OY.

Крива має 2 максимуми і 2 мінімуми. Їх координати:

таким чином (див. Рис . 1):
У декартовій системі координат

, де вісь абсцис направлена ​​по OX , а вісь ординат по OD , задана фіксована точка A на осі OX . Через т. А проводиться довільна пряма AL , яка перетинає вісь ординат у точці P. Від точки P , на відстані рівному OP , в обидві сторони вздовж прямої AL знаходяться точки M1 і M2 . Геометричне місце точок M1 і M2 утворюють строфоїди .
У прямокутній системі координат будується пряма строфоїди або просто строфоїди , яка зображена на Рис.1 . У косокутній системі координат будується коса строфоїди - Рис.2 .

Рис . 1

Рис.2 .

крива, геометричне місце точок M, для яких виконується співвідношення

,де OA - діаметр кола, BC - полухорда цієї окружності, перпендикулярна OA.

верзьєра Аньєзі

Декартов лист - плоска алгебраїчна крива третього порядку, яка задовольняє рівнянню в прямокутній системі
Параметр 3a визначається як діагональ квадрата, сторона якого дорівнює найбільшою хорді петлі.

Декартов лист