- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Круги Эйлера
Содержание
- 2. Круги Эйлера
- 3. Множества
- 4. Множества. Множество – совокупность объектов,
- 5. Запись множества.Например мы имеем множество цветов: георгины, розы, пионы, лилии и ромашки.А={г, р, п, л, р}
- 6. Виды множествРавные множестваА={А, Е, Ё, И} =
- 7. Операции над множествами1) Пересечением множества А и
- 8. Операции над множествамиЗадания1. Даны множества: А =
- 9. Операции над множествами2) Объединением множеств А и
- 10. Операции над множествами Задания1. Даны множества: А
- 11. Операции над множествами3) Разность А и В
- 12. Задания1. Даны множества: А = {2; 4;
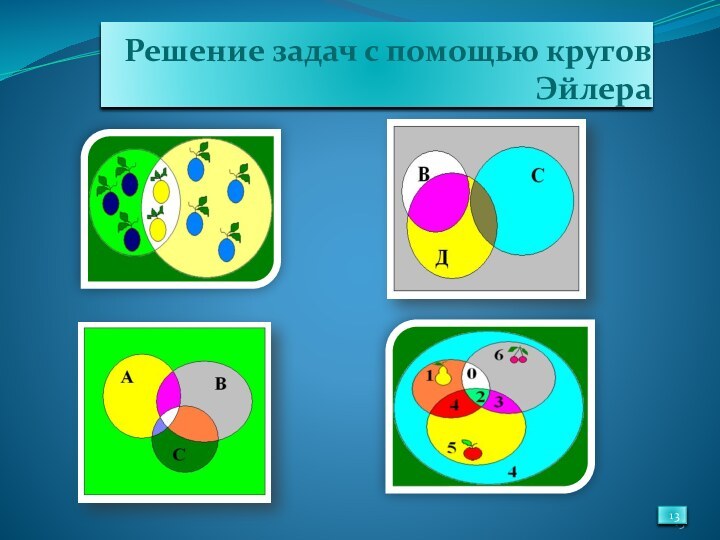
- 13. Решение задач с помощью кругов Эйлера
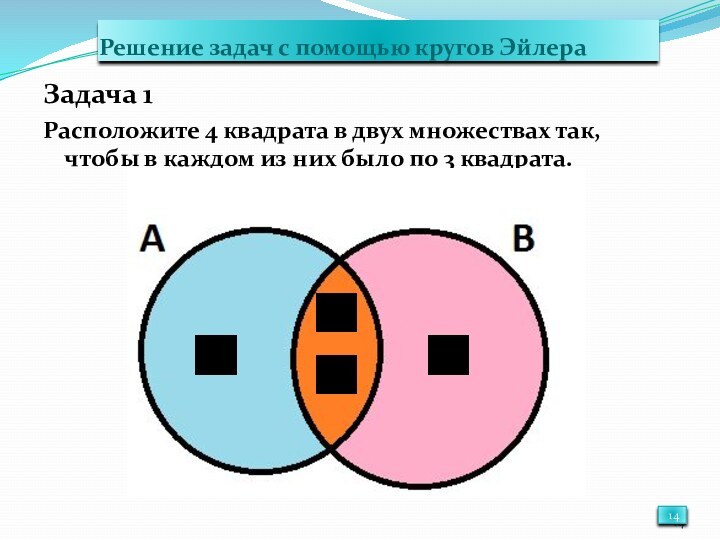
- 14. Решение задач с помощью кругов ЭйлераЗадача 1Расположите
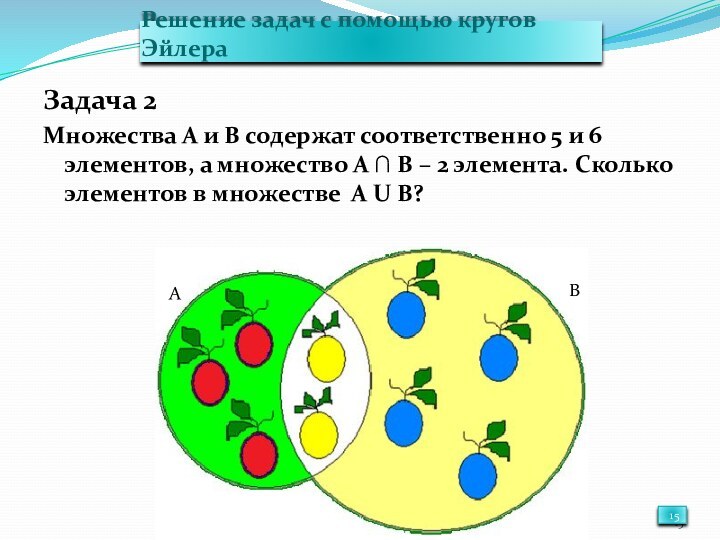
- 15. Решение задач с помощью кругов ЭйлераЗадача 2Множества
- 16. Скачать презентацию
- 17. Похожие презентации
Круги Эйлера










Слайд 4
Множества.
Множество – совокупность объектов, объединенных
каким либо признаком.
латинского алфавита: А, В, С, D и т. д. (множество животных, множество треугольников, множество людей и так далее).
Слайд 5
Запись множества.
Например мы имеем множество цветов: георгины, розы,
пионы, лилии и ромашки.
А={г, р, п, л, р}
Слайд 6
Виды множеств
Равные множества
А={А, Е, Ё, И} = В={Е,
А, И, Ё}
Конечные множества
А = {2; 3; 5; 7;
11; 13}Бесконечные множества
А={10; 20; 30; 40; 50; …}
Пустое множество обозначается символом Ø
Слайд 7
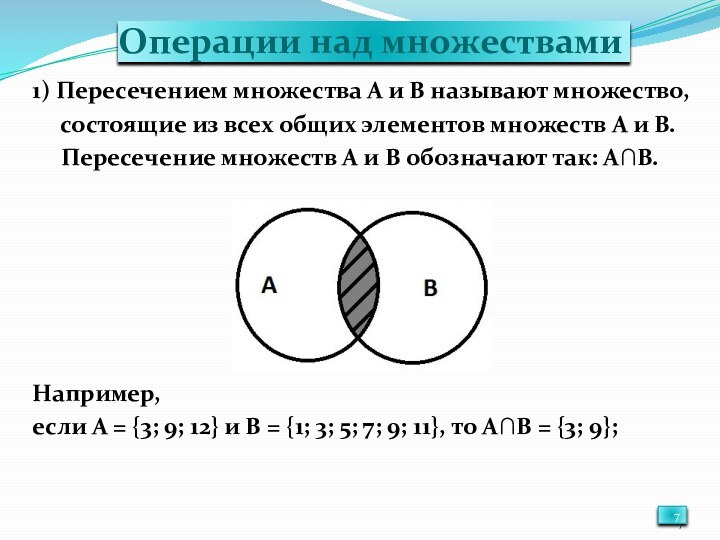
Операции над множествами
1) Пересечением множества А и В
называют множество,
состоящие из всех общих
элементов множеств А и В.Пересечение множеств А и В обозначают так: А∩В.
Например,
если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то А∩В = {3; 9};
Слайд 8
Операции над множествами
Задания
1. Даны множества: А = {2;
3; 8}, В = {2; 3; 8; 11},
С = {5; 11}.Найдите: 1) А∩В; 2) А∩С; 3) С∩В.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g, k}. Найдите (А∩В)∩С.
Слайд 9
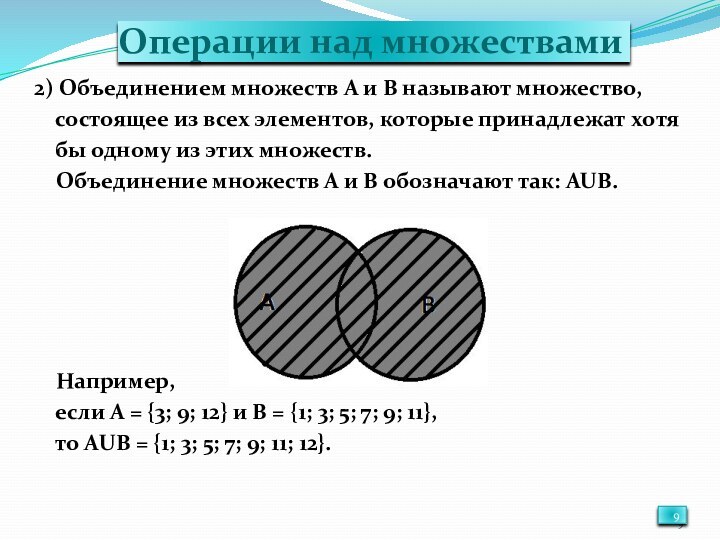
Операции над множествами
2) Объединением множеств А и В
называют множество,
состоящее из всех элементов, которые принадлежат
хотябы одному из этих множеств.
Объединение множеств А и В обозначают так: АUВ.
Например,
если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11},
то АUВ = {1; 3; 5; 7; 9; 11; 12}.
Слайд 10
Операции над множествами
Задания
1. Даны множества: А =
{2; 3; 8}, В = {2; 3; 8; 11},
С = {5; 11}.Найдите: 1) АUВ; 2) АUС; 3) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g, k}.
Найдите (АUВ)UС.
Слайд 11
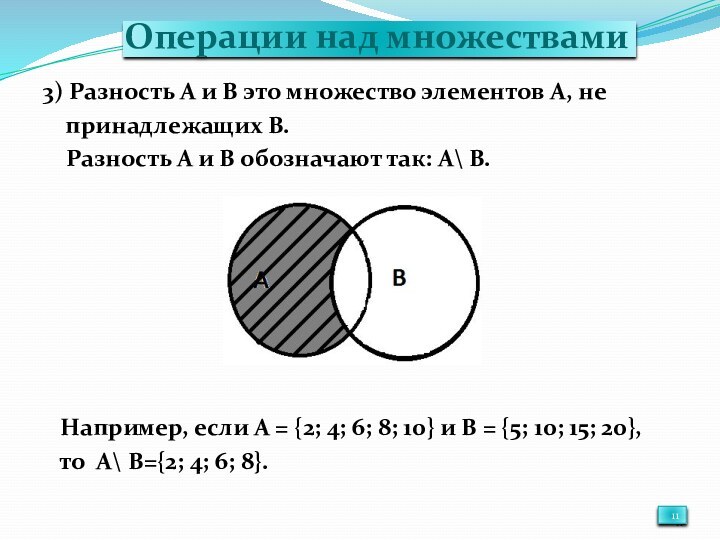
Операции над множествами
3) Разность А и В это
множество элементов А, не
принадлежащих В.
Разность А и В обозначают так: А\ В. Например, если А = {2; 4; 6; 8; 10} и В = {5; 10; 15; 20},
то А\ В={2; 4; 6; 8}.
Слайд 12
Задания
1. Даны множества: А = {2; 4; 7;
10}, В = {2; 3; 5;}, С = {2;
7; 10}.Найдите: 1) А \ В; 2) А \ С; 3) С \ В.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g}.
Найдите (А \ В) \ С.
Операции над множествами





























