Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Курсовая работа по математическим методам

Содержание

2. ВступлениеВ 1859 г. Сэр Вильям Гамильтон, знаменитый
3. Пример решенияПусть имеется граф, заданный матрицей смежности:Пусть имеется граф, заданный матрицей смежности:
4. Элемент матрицы сij будем считать стоимостью перелета из города i в
5. Приведем исходную матрицу по строкамИсходная:Выделенные жирным шрифтом числа в исходной матрице — это идеальный тур
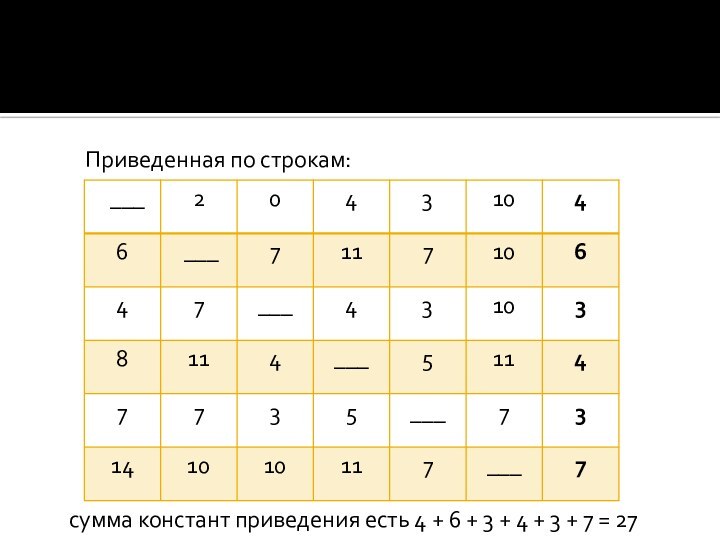
6. Приведенная по строкам:сумма констант приведения есть 4
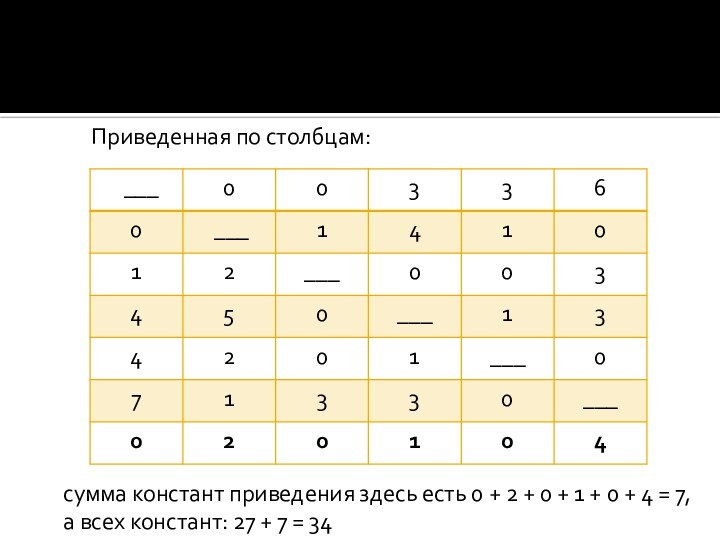
7. сумма констант приведения здесь есть 0 +
8. Теперь, тур, проходящий только через ребра нулевой
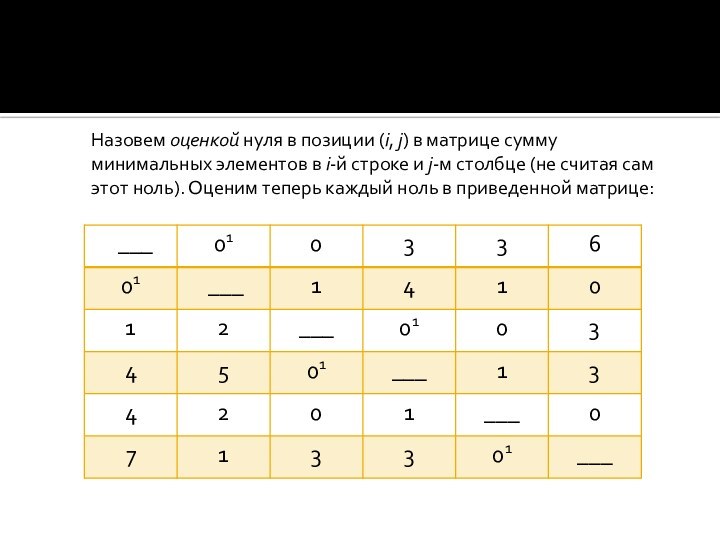
9. Назовем оценкой нуля в позиции (i, j) в матрице сумму
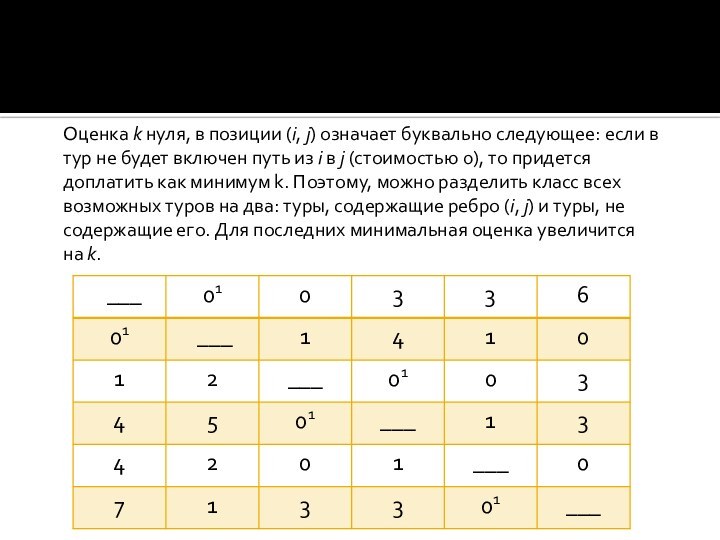
10. Оценка k нуля, в позиции (i, j) означает буквально следующее:
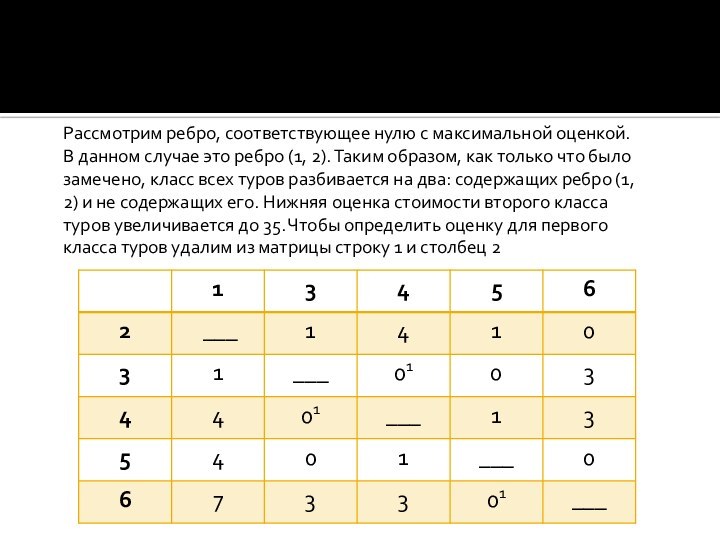
11. Рассмотрим ребро, соответствующее нулю с максимальной оценкой.
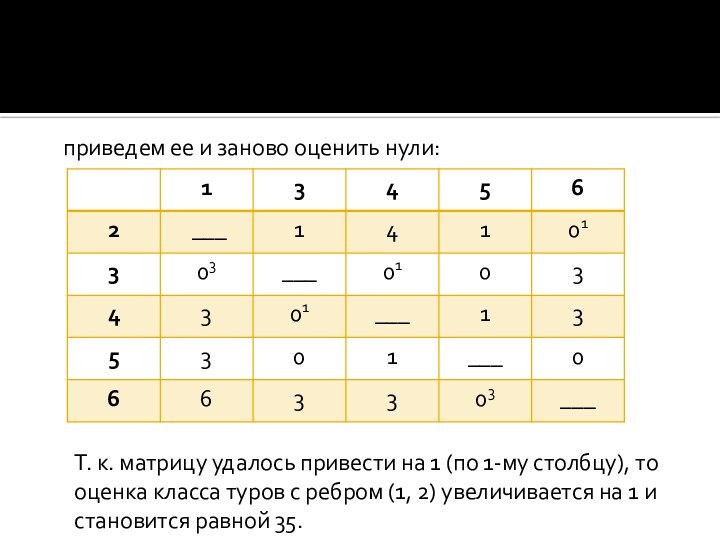
12. приведем ее и заново оценить нули:Т. к. матрицу
13. Скачать презентацию
14. Похожие презентации

ВступлениеВ 1859 г. Сэр Вильям Гамильтон, знаменитый математик, давший миру теорию комплексного числа , предложил детскую головоломку, в которой предлагалось совершить «круговое путешествие» по 20 городам, расположенных в различных частях земного шара. Каждый город соединялся дорогами

Главная
Разное
Курсовая работа по математическим методам

Курсовая работа по математическим методамТема: Решение Задачи коммивояжера методом ветвей и границ

ВступлениеВ 1859 г. Сэр Вильям Гамильтон, знаменитый математик, давший миру теорию комплексного

Пример решенияПусть имеется граф, заданный матрицей смежности:Пусть имеется граф, заданный матрицей смежности:

Элемент матрицы сij будем считать стоимостью перелета из города i в город j.Справедливо следующее: вычитая любую константу

Приведем исходную матрицу по строкамИсходная:Выделенные жирным шрифтом числа в исходной матрице — это идеальный тур

Приведенная по строкам:сумма констант приведения есть 4 + 6 + 3 +

сумма констант приведения здесь есть 0 + 2 + 0 + 1

Теперь, тур, проходящий только через ребра нулевой стоимости, будет, очевидно, минимальным. Для

Назовем оценкой нуля в позиции (i, j) в матрице сумму минимальных элементов в i-й строке и j-м

Оценка k нуля, в позиции (i, j) означает буквально следующее: если в тур не будет

Рассмотрим ребро, соответствующее нулю с максимальной оценкой. В данном случае это ребро

приведем ее и заново оценить нули:Т. к. матрицу удалось привести на 1 (по

Разбиение на классы и сами оценки можно представить в виде дерева:Таким образом,

Слайды презентации

Слайд 2 Вступление
В 1859 г. Сэр Вильям Гамильтон, знаменитый математик,

ВступлениеВ 1859 г. Сэр Вильям Гамильтон, знаменитый математик, давший миру теорию

давший миру теорию комплексного числа , предложил детскую головоломку,

в которой предлагалось совершить «круговое путешествие» по 20 городам, расположенных в различных частях земного шара. Каждый город соединялся дорогами с тремя соседними так, что дорожная сеть образовывала 30 ребер додекаэдра, в вершинах которого находились города a, b, … t. Обязательным условием являлось требование: каждый город за исключением первого можно посетить один раз.

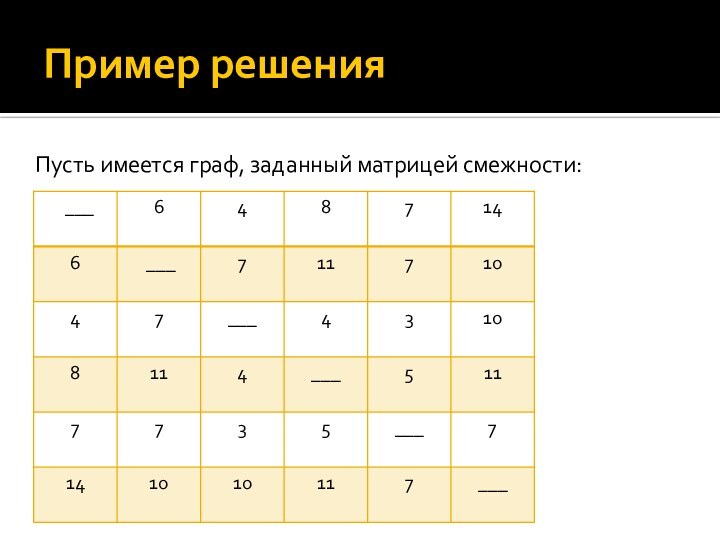
Слайд 3 Пример решения
Пусть имеется граф, заданный матрицей смежности:
Пусть имеется

граф, заданный матрицей смежности:

Слайд 4 Элемент матрицы сij будем считать стоимостью перелета из города i в город j.
Справедливо

Элемент матрицы сij будем считать стоимостью перелета из города i в город j.Справедливо следующее: вычитая любую

следующее: вычитая любую константу из всех элементов любой строки

или столбца матрицы С, оставляем минимальный тур минимальным. В связи с этим, процесс вычитания из каждой строки ее минимального элемента (приведение по строкам) не влияет на минимальный тур. Аналогично вводится понятие приведения по столбцам, обладающее тем же свойством.

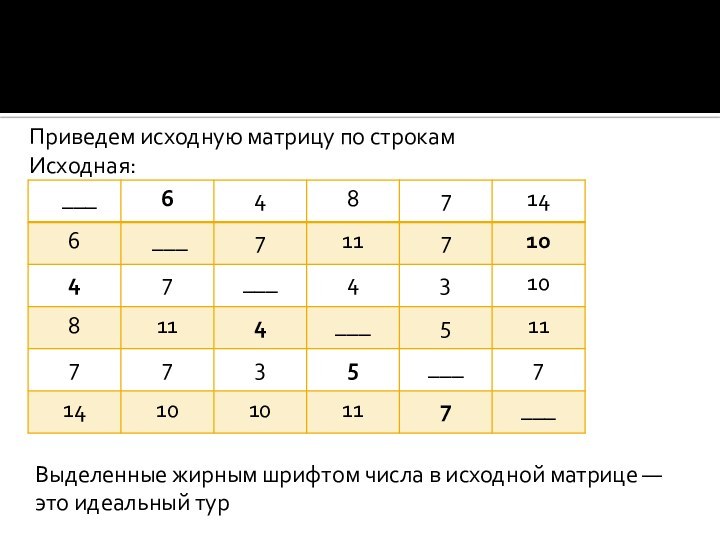
Слайд 5 Приведем исходную матрицу по строкам
Исходная:
Выделенные жирным шрифтом числа

в исходной матрице — это идеальный тур

Слайд 6 Приведенная по строкам:
сумма констант приведения есть 4 +

6 + 3 + 4 + 3 + 7

= 27

Слайд 7 сумма констант приведения здесь есть 0 + 2

сумма констант приведения здесь есть 0 + 2 + 0 +

+ 0 + 1 + 0 + 4 =

7, а всех констант: 27 + 7 = 34

Приведенная по столбцам:

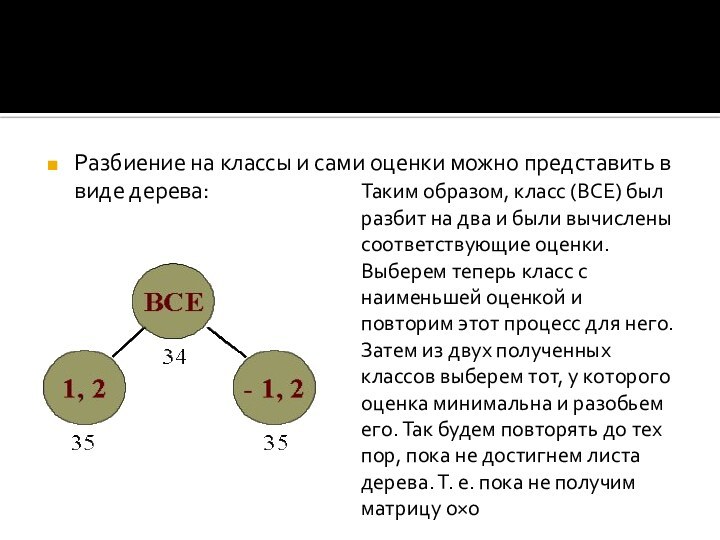
Слайд 8 Теперь, тур, проходящий только через ребра нулевой стоимости,

Теперь, тур, проходящий только через ребра нулевой стоимости, будет, очевидно, минимальным.

будет, очевидно, минимальным. Для того, чтобы определить его стоимость,

прибавим к нулю только что вычисленную константу 34: 0 + 34 = 34
Таким образом, мы получили нижнюю оценку стоимости класса всех возможных туров. Т. е. минимальный тур в данной задаче не может стоить меньше, чем 34.

Слайд 9 Назовем оценкой нуля в позиции (i, j) в матрице сумму минимальных

Назовем оценкой нуля в позиции (i, j) в матрице сумму минимальных элементов в i-й строке

элементов в i-й строке и j-м столбце (не считая сам этот

ноль). Оценим теперь каждый ноль в приведенной матрице:

Слайд 10 Оценка k нуля, в позиции (i, j) означает буквально следующее: если

Оценка k нуля, в позиции (i, j) означает буквально следующее: если в тур не

в тур не будет включен путь из i в j (стоимостью 0), то

придется доплатить как минимум k. Поэтому, можно разделить класс всех возможных туров на два: туры, содержащие ребро (i, j) и туры, не содержащие его. Для последних минимальная оценка увеличится на k.

Слайд 11 Рассмотрим ребро, соответствующее нулю с максимальной оценкой. В

Рассмотрим ребро, соответствующее нулю с максимальной оценкой. В данном случае это

данном случае это ребро (1, 2). Таким образом, как

только что было замечено, класс всех туров разбивается на два: содержащих ребро (1, 2) и не содержащих его. Нижняя оценка стоимости второго класса туров увеличивается до 35. Чтобы определить оценку для первого класса туров удалим из матрицы строку 1 и столбец 2