- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Л.4. ЗЕРКАЛЬНОЕ ОТРАЖЕНИЕ
Содержание
- 2. ЗЕРКАЛЬНОЕ ОТРАЖЕНИЕ ОТНОСИТЕЛЬНО ТОЧКИЗеркальное отражение от некоторой
- 3. Центральная симметрия
- 4. Таковы например, параллелограмм, окружность, плоскость и так
- 5. Построение многоугольника с нечетным числом сторон по серединам его сторон
- 6. Если произвольную точку Р1 той же плоскости
- 7. поэтому последний образ. то есть отрезокРп+1А1, лежит
- 8. Действительно, если зеркально отразить точку Р1 по
- 9. ЗЕРКАЛЬНОЕ ОТРАЖЕНИЕ ОТ ОСИЗеркальное отражение от оси
- 10. Осевая симметрия
- 11. Прямая и ее зеркальный образ относительно оси
- 12. В природе симметричные или по крайней мере
- 13. На плоскости осью симметрии отрезка прямой является
- 14. Отметим, что совокупность или множество точек, обладающих
- 15. Кратчайший путь из А и В, касающийся прямой e
- 16. Рассмотрим на плоскости прямую e и точки
- 17. Очевидно, что это отрезок прямой, соединяющий А'
- 18. Нетрудно заметить, что построенный таким образом кратчайший
- 19. Определение вписанного треугольника с наименьшим периметром
- 20. Рассмотрим теперь остроугольный треугольник ABC. Пусть требуется
- 21. Если P' — зеркальное отражение точки P
- 22. Тем самым мы построили треугольник наименьшего периметра,
- 23. Периметр вписанного таким образом треугольника зависит, естественно,
- 24. Отсюда следует также, что угол P'CP" вдвое
- 25. Среди преобразований совмещения зеркальное отражение от оси
- 26. Последовательное отражение от пересекающихся осей равносильно повороту
- 27. Последовательное отражение от параллельных осей равносильно переносу
- 28. Среди преобразований совмещения зеркальное отражение от оси
- 29. Последовательное отражение от двух пересекающихся прямых равносильно
- 30. Скачать презентацию
- 31. Похожие презентации
ЗЕРКАЛЬНОЕ ОТРАЖЕНИЕ ОТНОСИТЕЛЬНО ТОЧКИЗеркальное отражение от некоторой точки (симметрия относительно точки) равносильна повороту вокруг этой точки на 180°. Это преобразование переводит всякую прямую в параллельную ей прямую. Фигура называется центрально-симметричной, если существует зеркальное отражение относительно некоторой


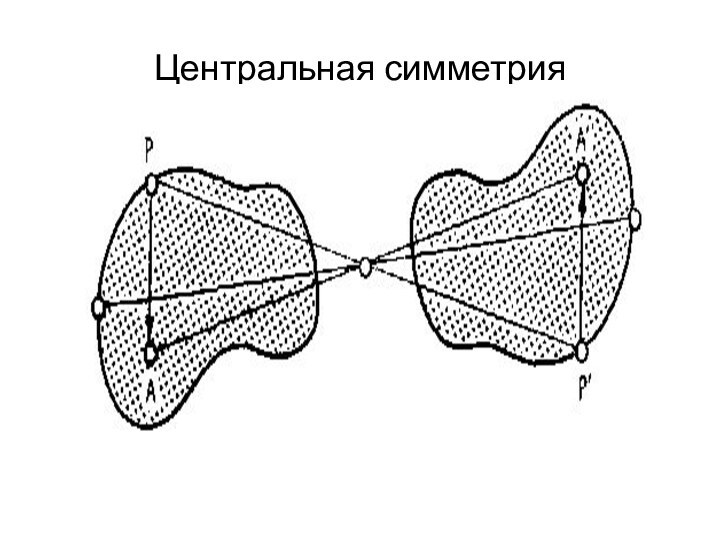





















Слайд 4
Таковы например, параллелограмм, окружность, плоскость и так далее.
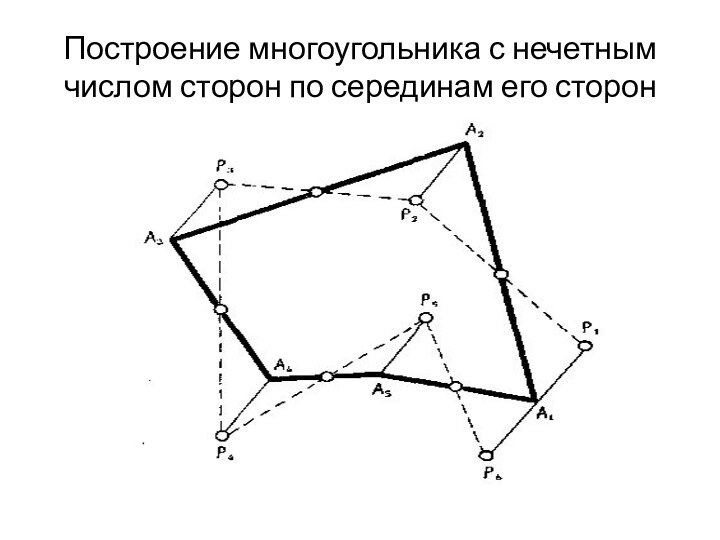
Рассмотрим
на плоскости некоторый многоугольник ALA2. . . Ап с
нечетным числом сторон (на рисунке изображен пятиугольник).Слайд 6 Если произвольную точку Р1 той же плоскости соединить
с точкой А1, а затем зеркально отразить отрезок Р1А1
по очереди от сере дин каждой из сторон многоуголь ника, то зеркальные образы Р2А2, Р3А3,. . ., РпАп будут равны и парал лельны отрезку Р1A1,
Слайд 7
поэтому последний образ. то есть отрезок
Рп+1А1, лежит на
одной прямой с отрезком Р1А1 причем точки Рп+1 и
Р1 расположены симметрично относительно точки A1 Это дает возможность построить многоугольник с нечетным числом сторон, если заданы лишь середины его сторон.Слайд 8 Действительно, если зеркально отразить точку Р1 по очереди
от середин всех сторон, то середина отрезка, соединяющего точку
Р1 с последним образом, окажется как раз вершиной А1 искомого многоугольника.
Слайд 9
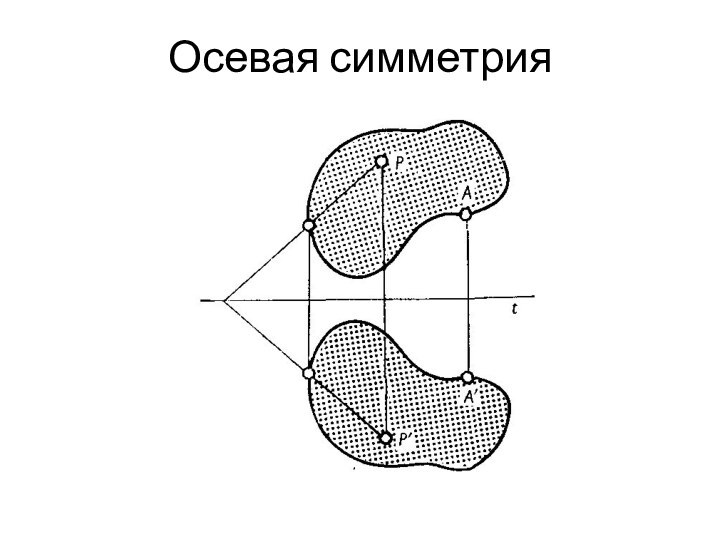
ЗЕРКАЛЬНОЕ ОТРАЖЕНИЕ ОТ ОСИ
Зеркальное отражение от оси является
таким преобразованием совмещения на плоскости, которое всякой фигуре ставит
в соответствие ее зеркальный образ относительно этой оси.Точки, между которыми устанавливается соответствие, лежат по разные стороны от оси на одинаковом расстоянии от нее; соединяющий их отрезок перпендикулярен оси.
Слайд 11 Прямая и ее зеркальный образ относительно оси пересекают
ось в одной точке или же параллельны ей.
Если существует
такое зеркальное отражение относительно некоторой оси, которое отображает фигуру на себя, то эта фигура называется симметричной. Таковы, например, прямая, окружность, квадрат и так далее. Слайд 12 В природе симметричные или по крайней мере приближенно
симметричные фигуры встречаются очень часто. Примером могут служить цветы,
листья и строение организмов живых существ.Такая симметрия часто используется в строительстве, в изобразительном искусстве, при изготовлении украшений и так далее. В геометрии также нередко применяются рассуждения, в которых симметрия играет весьма важную роль.
Слайд 13 На плоскости осью симметрии отрезка прямой является перпендикулярная
прямая, делящая отрезок пополам, а осью симметрии угла —
его биссектриса. Таким образом, совокупность точек, каждая из которых одинаково удалена от концов данного отрезка, есть перпендикулярная прямая, делящая отрезок пополам, а совокупность точек, каждая из которых одинаково удалена от сторон данного угла, есть биссектриса угла.Слайд 14 Отметим, что совокупность или множество точек, обладающих некоторым
общим свойством, часто называют геометрическим местом точек, обладающих данным
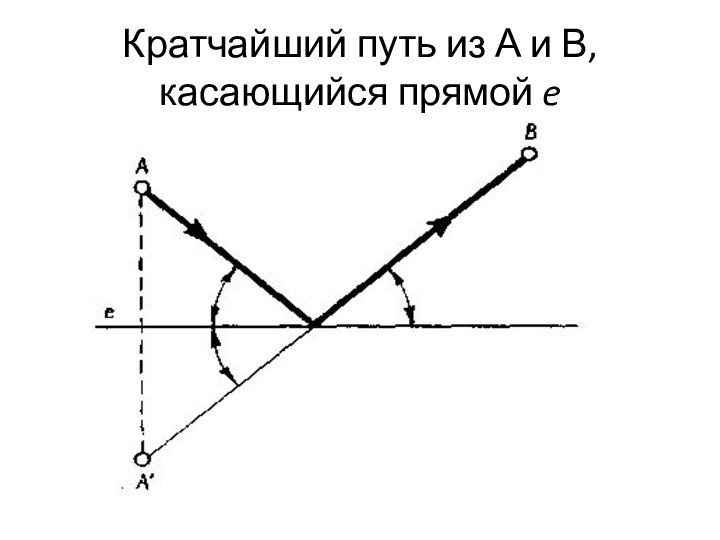
свойст вом. Так, например, ось симметрии отрезка прямой на плоскости является геометрическим местом точек, каждая из которых одинаково удалена от концов отрезка.Слайд 16 Рассмотрим на плоскости прямую e и точки А
и В, лежащие по одну сторону от этой прямой.
Определим кратчайший путь, ведущий от А до прямой, а затем в В. Для этого найдем кратчайший путь из точки А' (зеркального образа А относительно прямой e) в точку В.Слайд 17 Очевидно, что это отрезок прямой, соединяющий А' и
В. Наши рассуждения основаны на том, что расстояние от
точки А до любой точки прямой e равно расстоянию от ее зеркального образа А' до той же точки.Слайд 18 Нетрудно заметить, что построенный таким образом кратчайший путь
совпадает с траекторией светового луча, который, выходя из точки
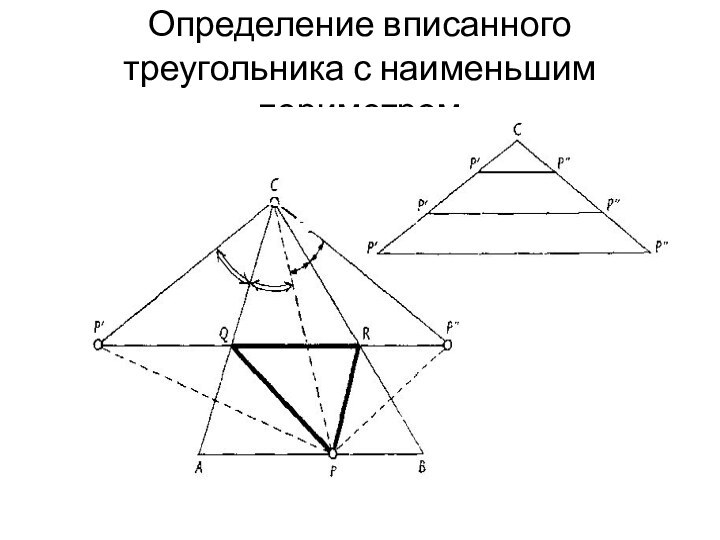
А, отражается от зеркала, проходящего через прямую e перпендикулярно плоскости, а затем попадает в В (угол падения равен углу отражения).Слайд 20 Рассмотрим теперь остроугольный треугольник ABC. Пусть требуется определить
кратчайший путь, ведущий из некоторой точки P стороны AB
к стороне АС, отсюда к стороне ВС , а затем обратно в точку Р. Воспользуемся методом, примененным выше.Слайд 21 Если P' — зеркальное отражение точки P относительно
стороны АС, а точка P" — относительно стороны ВС,
то искомый путь равен отрезку P'P". Этот отрезок пересекает стороны треугольника в точках Q и R, следовательно, кратчайшим путем является контур треугольника PQR.Слайд 22 Тем самым мы построили треугольник наименьшего периметра, вписанный
в данный треугольник (то есть его вершины лежат на
сторонах треугольника ABC) и удовлетворяющий тому условию, что одна из его вершин совпадает с данной точкой Р.Слайд 23 Периметр вписанного таким образом треугольника зависит, естественно, от
выбора точки Р. Если мы теперь хотим определить положение
точки P, при котором треугольник PQR имеет наименьший периметр, то следует принять во внимание, что стороны CP' и CP" треугольника P'CP" являются зеркальными образами отрезка CP, то есть равны между собой.Слайд 24 Отсюда следует также, что угол P'CP" вдвое больше,
чем угол ACBтреугольника ABC, то есть не зависит от
выбора точки Р. Следовательно, наименьший периметр имеет тот из треугольников P'CP", который имеет наименьшее ребро, то есть для которого соответствующий отрезок CP имеет наименьшую длину.Слайд 25 Среди преобразований совмещения зеркальное отражение от оси играет
особую роль. Любое преобразование совмещения может быть получено в
результате последовательного выполнения нескольких зеркальных отражений (то есть как произведение нескольких зеркальных отражений).Слайд 28 Среди преобразований совмещения зеркальное отражение от оси играет
особую роль. Любое преобразование совмещения может быть получено в
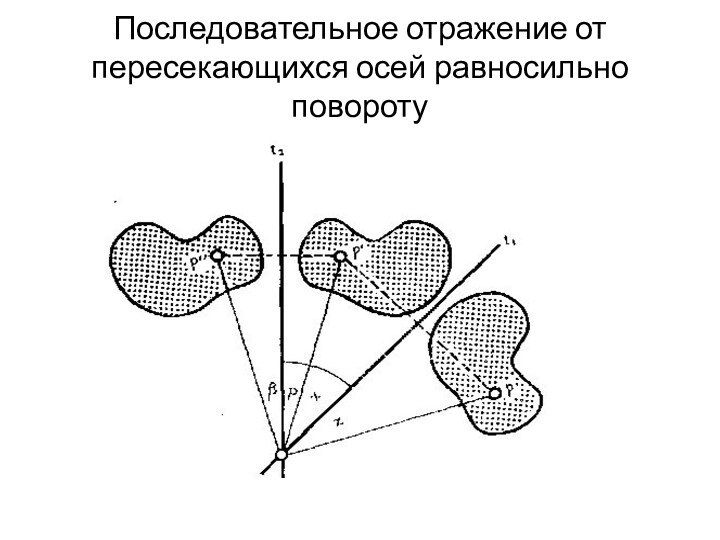
результате последовательного выполнения нескольких зеркальных отражений (то есть как произведение нескольких зеркальных отражений).Слайд 29 Последовательное отражение от двух пересекающихся прямых равносильно повороту
вокруг точки их пересечения на угол, вдвое превышающий угол
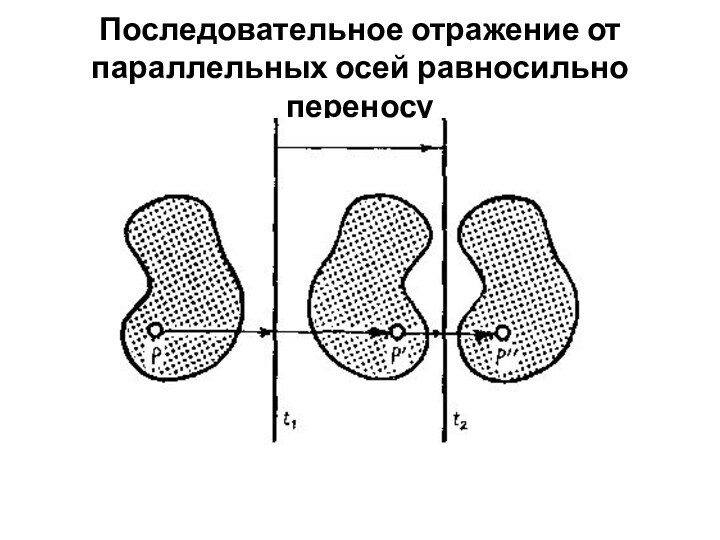
между этими прямыми.Произведение отражений от двух параллельных осей равносильно переносу в направлении, перпендикулярном осям, на расстояние, вдвое превышающее расстояние между ними.





























