которые изменяют лишь положение фигур (тел) в пространстве, преобразования
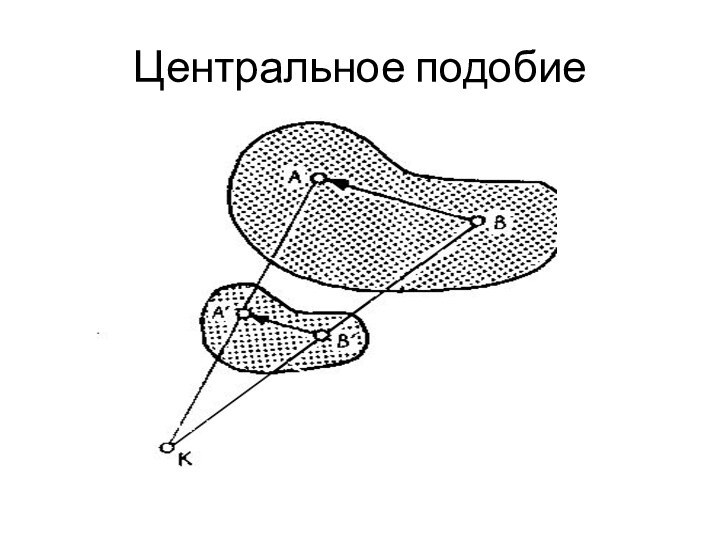
подобия вызывают большие изменения.Преобразованием подобия мы называем такое преобразование, при котором отношение образа любого отрезка к самому отрезку постоянно. Это отношение называется коэффициентом подобия.