Слайд 3
Понятие числовой функции
Переменная х называется аргументом функции или
независимой переменной, а у — значением функции или зависимой
переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости.
Множество X называется областью определения функции f и обозначается D(f). Множество всех у называется множеством значений функции f и обозначается E(f)
Если переменные x и y рассматривать, как декартовы координаты, то графиком функции у = f(x) называется множество точек координатной плоскости ОXY с координатами (x,y).
Слайд 5
Способы задания функций
Табличный способ: функция задается таблицей ряда
значений аргумента и соответствующих значений функции.
На практике часто приходится
пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.
Графический способ: задается график функции. Преимуществом графического задания является его наглядность, недостатком — его неточность
Слайд 11
Свойства Обратной функции
Если функция x=f-1(y) является обратной для
функции y=f(x) , то функция y=f(x) будет обратной для
функции x=f-1(y) .
Т.е. функции y=f(x) и x=f-1(y) являются взаимно обратными.
Область определения функции y=f(x) является множеством значений функции x=f-1(y), а множество значений функции y=f(x) - областью определения функции x=f-1(y)
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов координатной плоскости OXY
Слайд 17
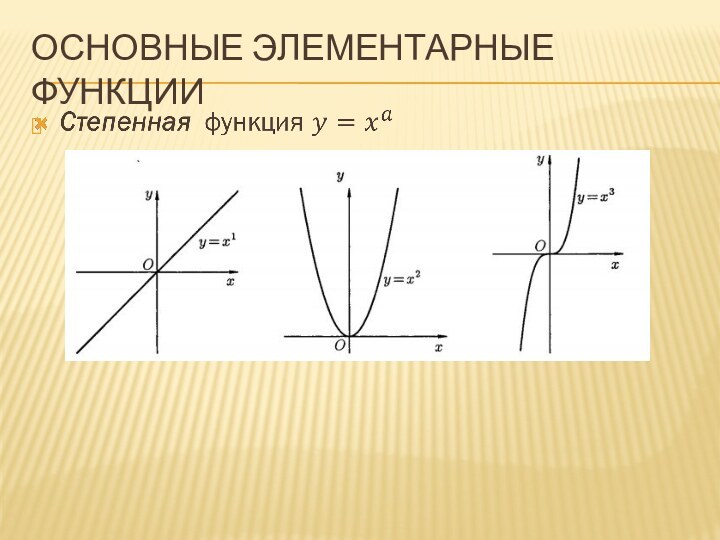
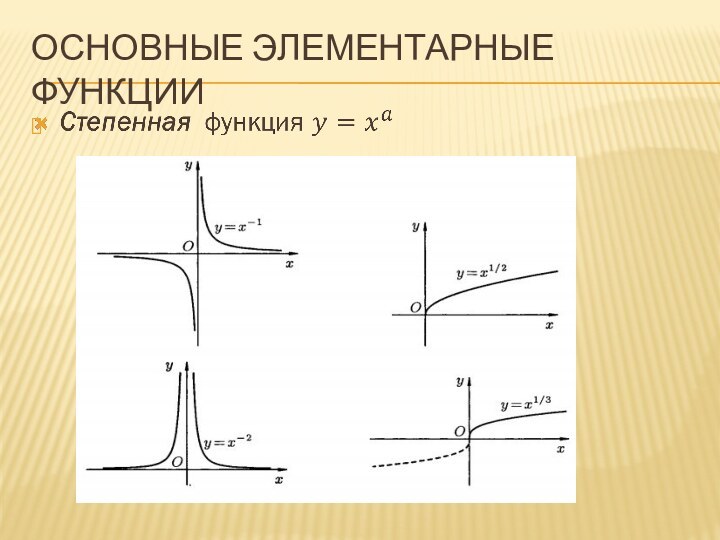
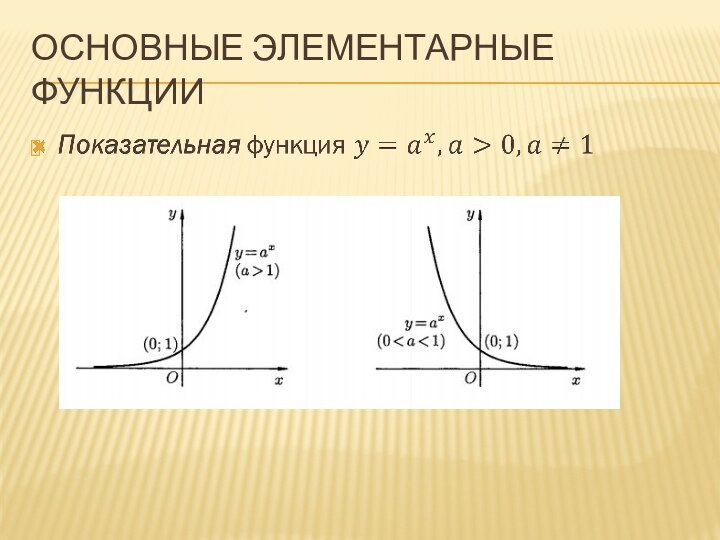
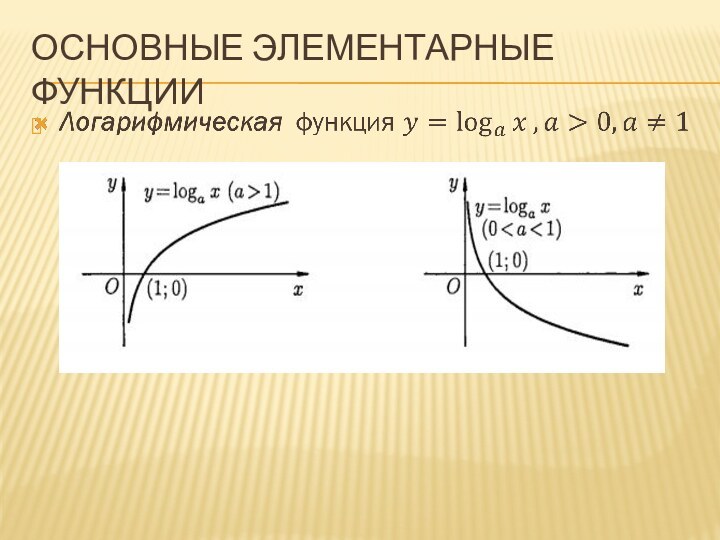
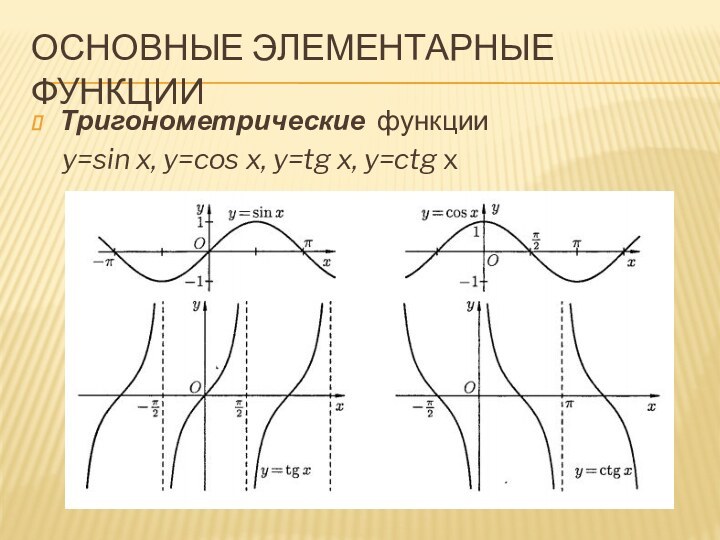
Основные Элементарные функции
Тригонометрические функции
y=sin x,
y=cos x, y=tg x, y=ctg x
Слайд 18
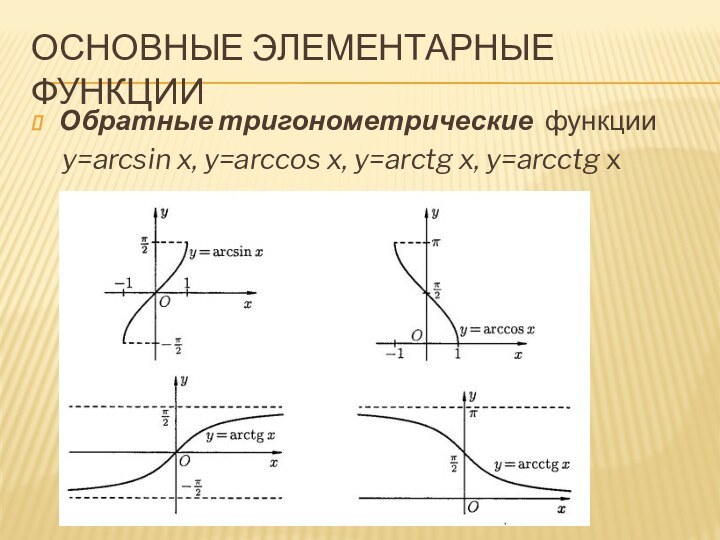
Основные Элементарные функции
Обратные тригонометрические функции
y=arcsin
x, y=arccos x, y=arctg x, y=arcctg x
Слайд 21
Генрих Эдуард Гейне (Heinrich Eduard Heine)
(1821-1881) — немецкий математик.
Ученик Дирихле.
Изучал математику в Гёттингенском университете, Берлинском университете
и в Альбертине в Кёнигсберге, был профессором математики
в Бонне и в Галле.
Занимался теорией потенциала, теорией функций и дифференциальными уравнениями
Слайд 23
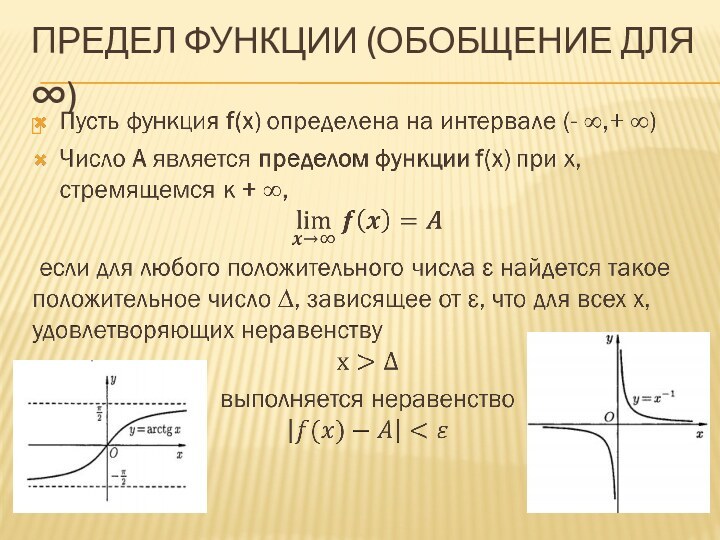
Предел функции (обобщение для ∞)
Слайд 24
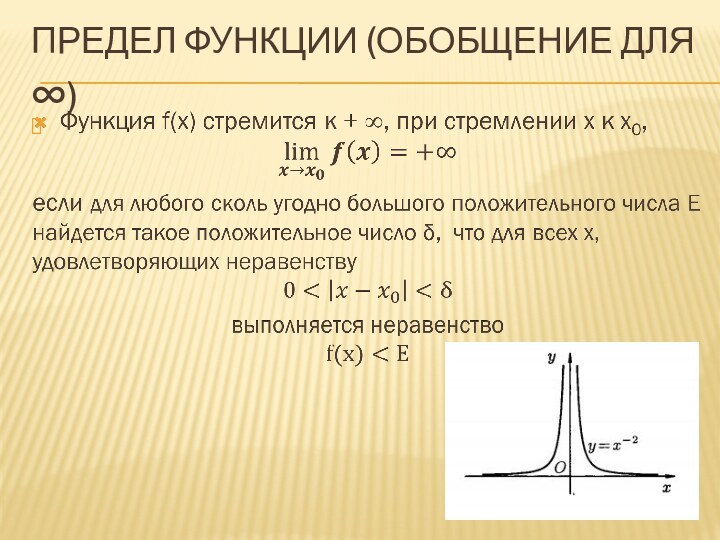
Предел функции (обобщение для ∞)
Слайд 29
Следствия Теорем о пределах функций
Слайд 39
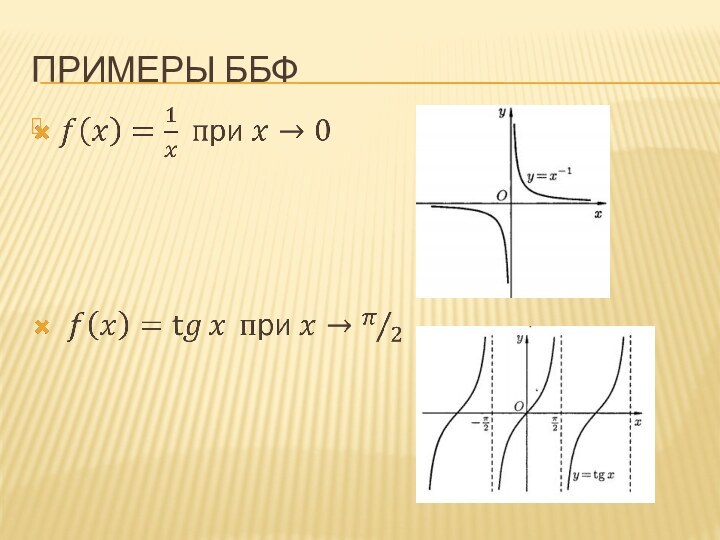
Теоремы о бесконечно малых функциях
Слайд 40
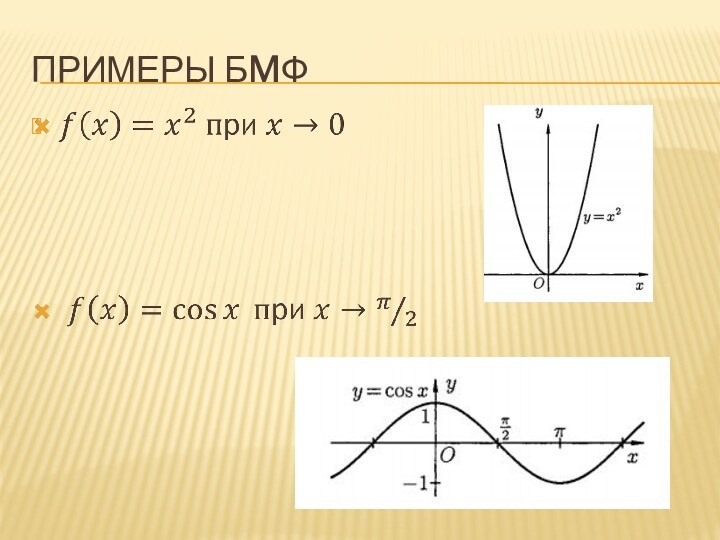
Сравнение бесконечно малых функций
Две БМФ сравниваются между собой
с помощью их отношения.
Как известно, сумма, разность и произведение
двух БМФ. есть БМФ. Отношение же двух БМФ может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Слайд 41
Сравнение бесконечно малых функций
Слайд 42
Эквивалентные бесконечно малые функции
Слайд 43
Основные Эквивалентные бесконечно малые функции