- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Лекция 7. Управление портфелем финансовых инструментов
Содержание
- 2. Понятие портфеля активовПортфель — это набор финансовых
- 3. Подходы к формированию портфелятрадиционный современный.Традиционный основывается на
- 4. Теория Марковицаподход, основанный на анализе ожидаемых средних
- 5. ОЖИДАЕМАЯ ДОХОДНОСТЬ ПОРТФЕЛЯгде: Е(rр) — ожидаемая доходность
- 6. ОЖИДАЕМАЯ ДОХОДНОСТЬ ПОРТФЕЛЯ
- 7. ПримерПример.Портфель состоит из двух активов А и
- 8. Доходность акции с учетом вероятности
- 9. Запишем формулу определения ожидаемой доходности актива в
- 10. ОЖИДАЕМЫЙ РИСК АКТИВАОпределяется при помощи дисперсии и стандартного отклонения(волатильность).r—доходность актива;
- 11. Доходность актива в том или ином году
- 12. НапримерДва актива имеют одинаковую ожидаемую доходность, которая
- 13. ОЖИДАЕМЫЙ РИСК ПОРТФЕЛЯОжидаемый риск портфеля представляет собой
- 14. Риск портфеля зависит от того, в каком
- 15. Пример
- 17. ПримерРассмотрим упрощенную экономическую систему, в которой на
- 18. Пример
- 19. Теория МарковицаОжидаемый доход портфеля, который поровну распределен
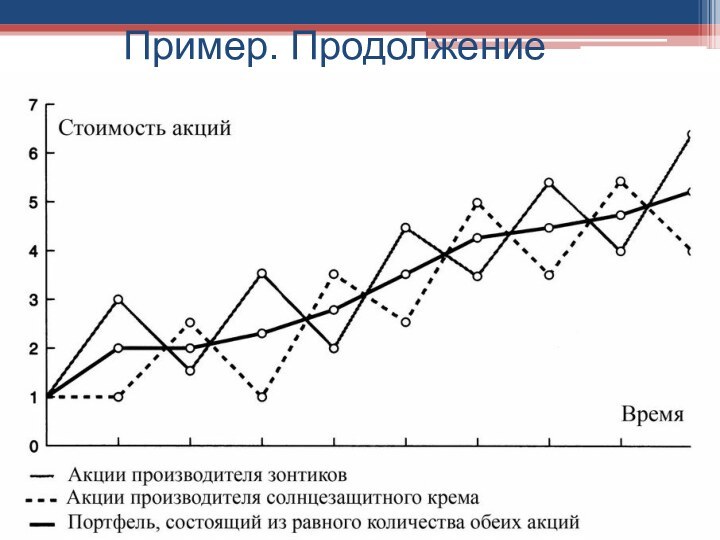
- 20. Пример. Продолжение
- 21. Практическое применение теории Марковица Формирование инвестиционного портфеля
- 22. РИСК ПОРТФЕЛЯ, СОСТОЯЩЕГО ИЗ ДВУХ АКТИВОВгде: σр2
- 23. Пример.Определить риск портфеля, состоящего из бумаг А
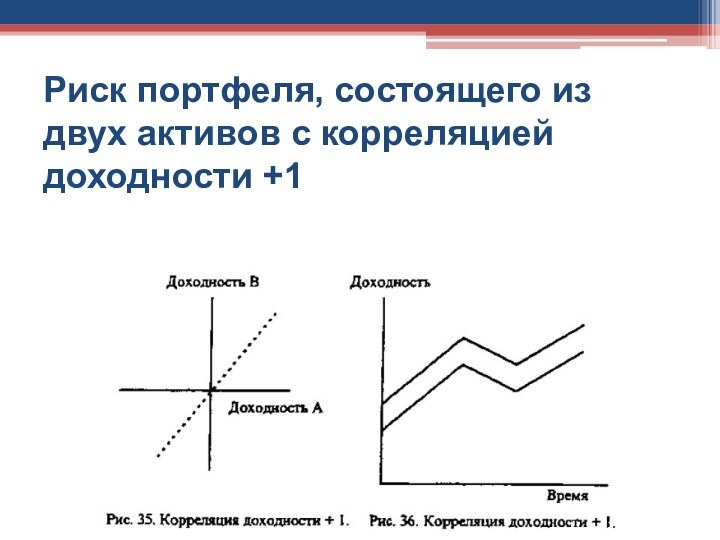
- 25. Риск портфеля, состоящего из двух активов с корреляцией доходности +1
- 26. Таким образом, если доходности активов имеют корреляцию
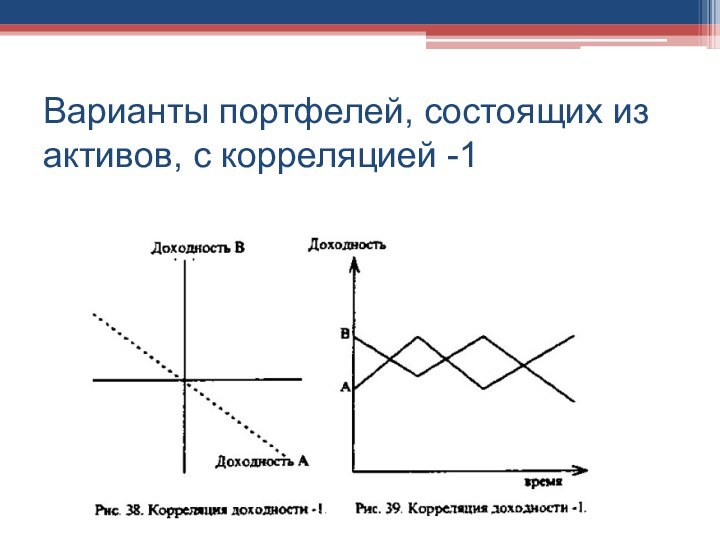
- 27. Риск портфеля, состоящего из двух активов с корреляцией доходности -1
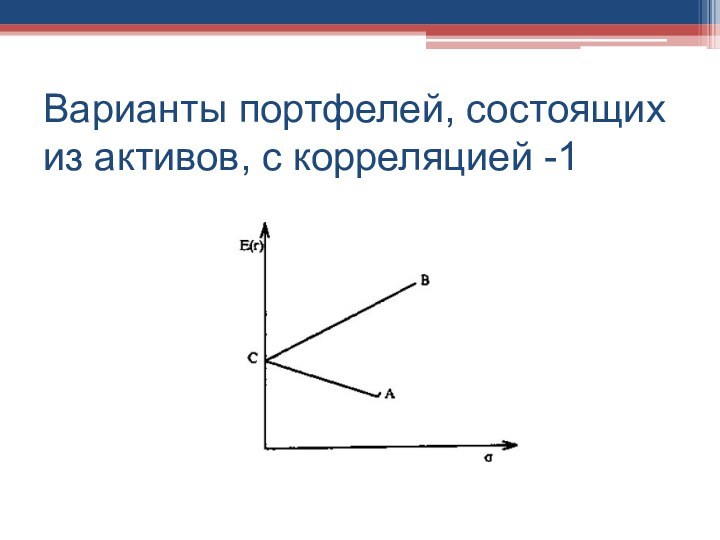
- 28. Варианты портфелей, состоящих из активов, с корреляцией -1
- 29. Варианты портфелей, состоящих из активов, с корреляцией -1
- 31. ПримерσA = 0,0268; σв = 0,0350.
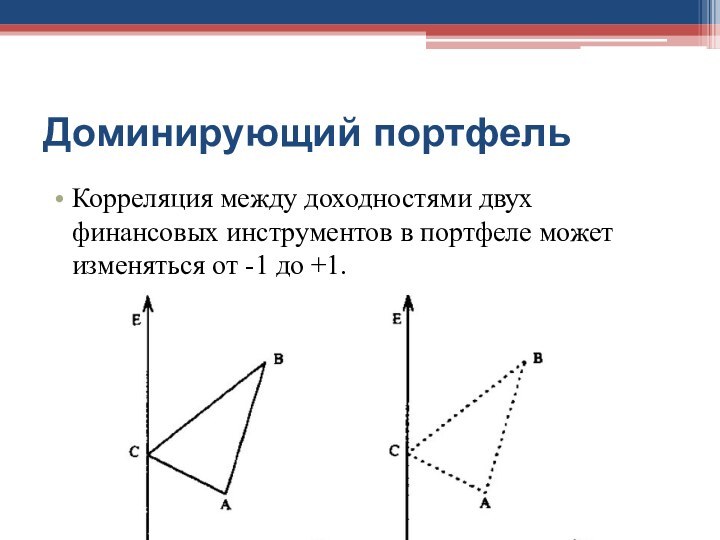
- 33. Доминирующий портфельКорреляция между доходностями двух финансовых инструментов в портфеле может изменяться от -1 до +1.
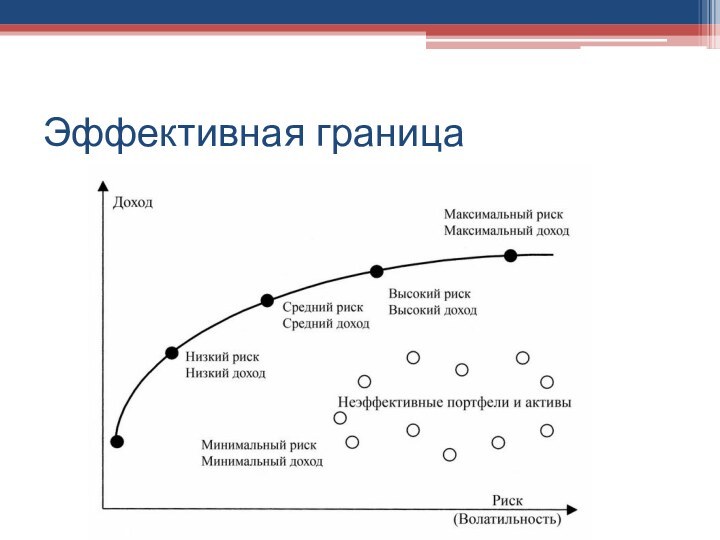
- 34. Эффективная граница
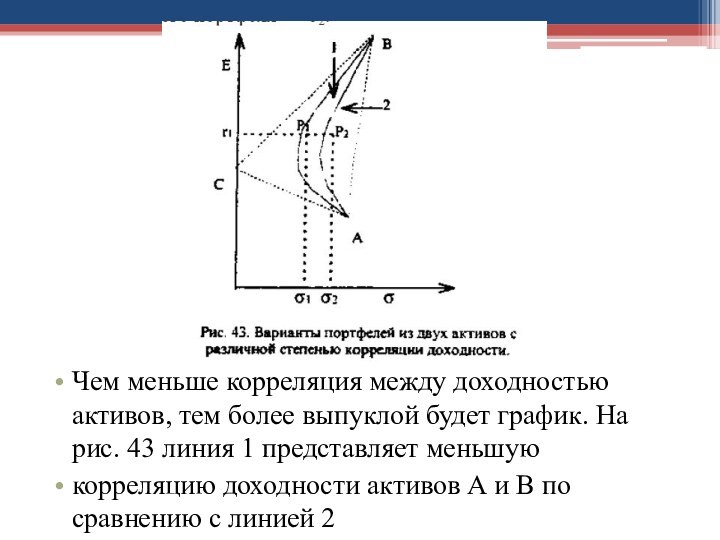
- 35. Чем меньше корреляция между доходностью активов, тем
- 36. Однако рациональный инвестор остановит свой выбор только
- 37. Если инвестор формирует портфель из двух активов,
- 38. Риск портфеля, состоящего из двух активов с некоррелируемыми доходностями
- 39. Пример. Рассчитать риск портфеля
- 41. Общие выводы1) Если в портфель объединяются активы
- 42. Общие выводы3) Чем меньше корреляция доходности активов,
- 43. Скачать презентацию
- 44. Похожие презентации
Понятие портфеля активовПортфель — это набор финансовых активов, которыми располагает инвестор.Главная цель формирования портфеля состоит в стремлении получить требуемый уровень ожидаемой доходности при более низком уровне ожидаемого риска.

































Слайд 2
Понятие портфеля активов
Портфель — это набор финансовых активов,
которыми располагает инвестор.
получить требуемый уровень ожидаемой доходности при более низком уровне ожидаемого риска.
Слайд 3
Подходы к формированию портфеля
традиционный
современный.
Традиционный основывается на фундаментальном
и техническом анализе.
Современный основан на использовании статистических и математических
методов подбора финансовых инструментов в портфель, а также на ряде новых концептуальных подходов.
Слайд 4
Теория Марковица
подход, основанный на анализе ожидаемых средних значений
и вариаций случайных величин.
Разработанная Гарри Марковицем методика формирования
инвестиционного портфеля, направленная на оптимальный выбор активов исходя из требуемого соотношения доходность/риск
Слайд 5
ОЖИДАЕМАЯ ДОХОДНОСТЬ ПОРТФЕЛЯ
где: Е(rр) — ожидаемая доходность портфеля;
Е(r1);
Е(r2); Е(rn) — ожидаемая доходность соответственно первого, второго и
n-го активов;θ1; θ2; θn — удельный вес в портфеле первого, второго и n-го активов.
Слайд 7
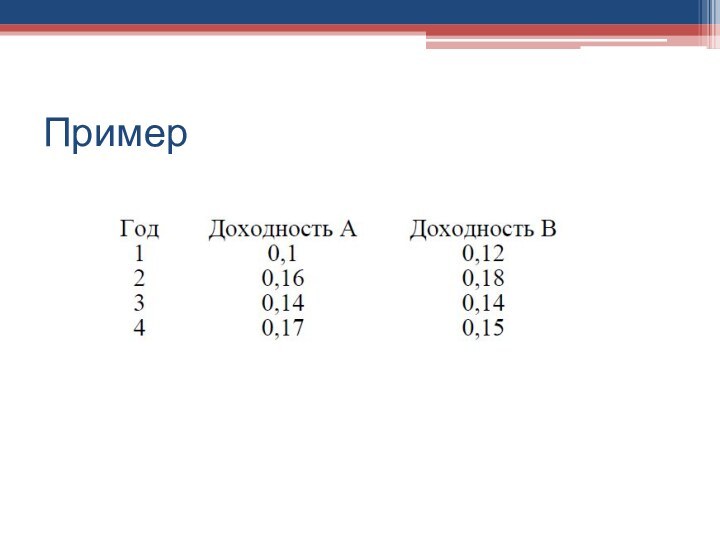
Пример
Пример.
Портфель состоит из двух активов А и В.
Е(RА) = 15%, Е(rB) = 10%.
Стоимость актива А —
300 тыс. руб., актива В — 700 тыс. руб. Необходимо определить ожидаемую доходность портфеля.
Слайд 9
Запишем формулу определения ожидаемой доходности актива в
общем виде:
где:
Е(r) — ожидаемая доходность актива;
E(ri ) — ожидаемая доходность
актива в i-м случае;πi — вероятность получения доходности в i-м случае.
Слайд 10
ОЖИДАЕМЫЙ РИСК АКТИВА
Определяется при помощи дисперсии и стандартного
отклонения(волатильность).
r—доходность актива;
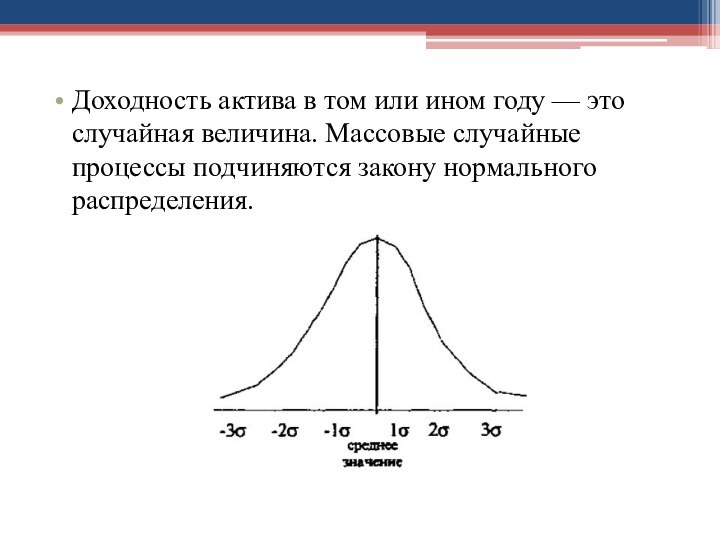
Слайд 11 Доходность актива в том или ином году —
это случайная величина. Массовые случайные процессы подчиняются закону нормального
распределения.
Слайд 12
Например
Два актива имеют одинаковую ожидаемую доходность, которая равна
50%. Однако стандартное отклонение первого актива составляет 5%, а
второго — 10%.Это говорит о том, что второй актив рискованнее первого, так как существует 68, 3% вероятности, что через год доходность первого актива может составить от 45% до 55%, а второго — от 40% до 60% и т. д.
Слайд 13
ОЖИДАЕМЫЙ РИСК ПОРТФЕЛЯ
Ожидаемый риск портфеля представляет собой сочетание
стандартных отклонений (дисперсий) входящих в него активов.
В отличие от
ожидаемой доходности портфеля его риск не является обязательно средневзвешенной величиной стандартных отклонений (дисперсий) доходностей активов.Слайд 14 Риск портфеля зависит от того, в каком направлении
изменяются доходности входящих в него активов при изменении конъюнктуры
рынка и в какой степени.Для этого используют такие показатели как ковариация и коэффициент корреляции.
Слайд 17
Пример
Рассмотрим упрощенную экономическую систему, в которой на бирже
продаются акции только двух компаний: производителя солнцезащитного крема и
производителя зонтиков.
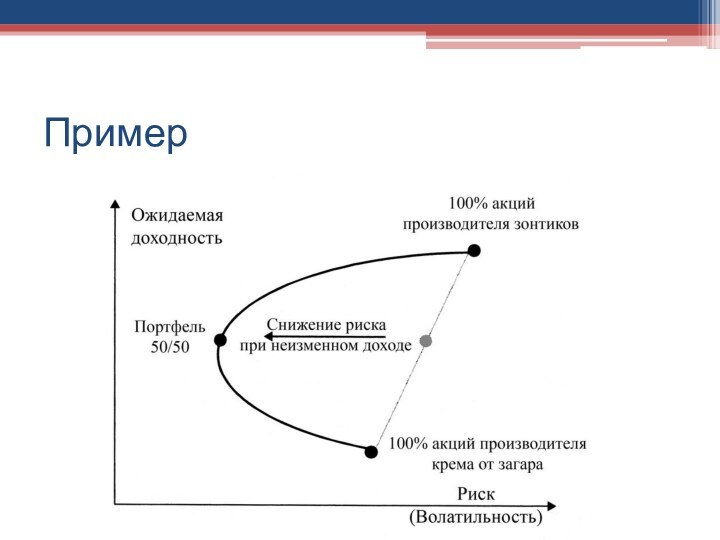
Слайд 19
Теория Марковица
Ожидаемый доход портфеля, который поровну распределен между
акциями двух компаний, равен среднему значению доходов входящих в
него акций.Волатильность портфеля значительно меньше средней волатильности двух акций и значительно меньше волатильности составляющих портфеля.
Слайд 21
Практическое применение теории Марковица
Формирование инвестиционного портфеля на
основе
доли активов в общем портфеле;
ожидаемой доходность каждого из активов
портфеля;волатильности активов портфеля;
коэффициента корреляции между активами портфеля.
Слайд 22
РИСК ПОРТФЕЛЯ, СОСТОЯЩЕГО ИЗ ДВУХ АКТИВОВ
где: σр2 —
риск(дисперсия) портфеля;
θA — уд. вес актива А в портфеле;
θB
— уд. вес актива В в портфеле;СovA, B — ковариация доходности активов А и В.
Слайд 23
Пример.
Определить риск портфеля, состоящего из бумаг А и
В, если θA =0, 3; θB = 0, 7;
σA2 = 0, 0007188; σB2 = 0, 0004688; COVA, B = 0, 0004562.
Слайд 26
Таким образом, если доходности активов имеют корреляцию +1,
то риск портфеля — это средневзвешенный риск входящих в
него активов.
Слайд 33
Доминирующий портфель
Корреляция между доходностями двух финансовых инструментов в
портфеле может изменяться от -1 до +1.
Слайд 35
Чем меньше корреляция между доходностью активов, тем более
выпуклой будет график. На рис. 43 линия 1 представляет
меньшуюкорреляцию доходности активов А и В по сравнению с линией 2
Слайд 36
Однако рациональный инвестор остановит свой выбор только на
верхней части данной кривой, а именно,отрезке DB, поскольку на
нем расположены портфели, которые приносят более высокий уровень ожидаемой доходности при том же риске по сравнению с портфелями на участке DA.Слайд 37 Если инвестор формирует портфель из двух активов, А
и В, как показано, то в точке D он
может получить для сочетания данных активов портфель с наименьшим уровнем риска. Чтобы его сформировать, необходимо найти удельные веса в портфеле активовА и В.
Слайд 41
Общие выводы
1) Если в портфель объединяются активы с
корреляцией +1, то достигается только усреднение, а не уменьшение
риска;2) Если в портфель объединяются активы с корреляцией меньше,чем +1, то его риск уменьшается. Уменьшение риска портфеля достигается при сохранении неизменного значения ожидаемой доходности
Слайд 42
Общие выводы
3) Чем меньше корреляция доходности активов, тем
меньше риск портфеля;
4) Если в портфель объединяются активы с
корреляцией -1, то можно сформировать портфель без риска;5) При формировании портфеля необходимо стремиться объединить в него активы с наименьшей корреляцией.