Презентация на тему Механические колебания

повторяющиеся процессы, например, процесс работы сердца.
Аналогично и в

технике есть разнообразные повторяющиеся процессы
Все эти явления подчиняются общим закономерностям, которые мы рассмотрим на примере механических колебаний.

Колебания – это периодически повторяющиеся движения или изменения параметров, которые характеризуют состояние системы.
Колебания могут быть разной природы:
механические,
тепловые,
электрические и т. п.
Виды колебаний
гармонические,
периодические
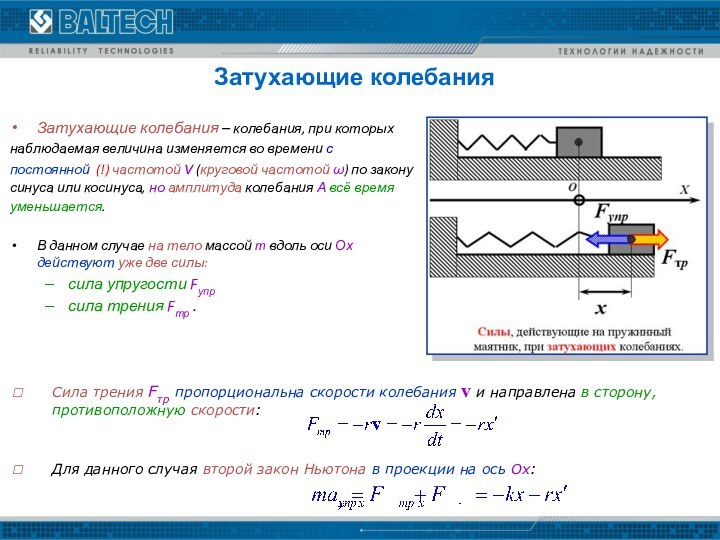
затухающие,
вынужденные
Простейшим видом колебаний является гармонические колебания, но чаще встречаются периодические колебания.

Систему, совершающую колебательные движения, называют осциллятором.

на которое отклоняется колеблющееся тело в данный момент времени

от положения равновесия. Измеряется в СИ в метрах (м);
для гармонического колебания (1):

А– максимальное смещение (А0=xмах) от положения равновесия. Измеряется в

СИ в метрах (м);

Период Т – время одного полного колебания. Измеряется в СИ в секундах (с).
Для колебания материальной точки на пружине:
Где m – масса материальной точки, закреплённой на пружине жёсткостью k.

Частота или линейная частота ν («ню») – это число колебаний в единицу времени.
Измеряется в СИ в Герцах (Гц) или обратных секундах:

Связана с периодом Т формулой:

которая связана с линейной частотой  формулой:

Измеряется в СИ

в радианах в секунду (рад/с), т.к. по определению -это скорость изменения угла φ от времени t.
Круговая частота ω связана с коэффициентом жёсткости k:





Фаза колебаний φ («фи») характеризует состояние колеблющейся материальной точки в любой момент времени: где φ0 - начальная фаза колебаний (фаза при t0=0).

Основные характеристики колебательного движения

Фаза по смыслу является углом отклонения от положения равновесия и измеряется в угловых градусах (внесистемная единица) и в СИ – в радианах (рад).
Амплитуда А0 и начальная фаза φ0 колебаний определяются начальными условиями движения (положением материальной точки в момент времени t0 = 0).

случаях для синих кривых φ0 = 0:
а – красная кривая

отличается от синей только бóльшей амплитудой (x‘max > xmax);

b – красная кривая отличается от синей только значением периода (T' = T / 2);

с – красная кривая отличается от синей только значением начальной фазы:

v.
Измеряется в СИ в метрах в секунду (м/с).

Выражение для v найдится путем дифференцирования х:
Скорость максимальна, если: Тогда


Ускорение колеблющейся материальной точки а.
Измеряется в СИ в метрах в секунду в квадрате (м/с2).
Выражение для а найдится путем дифференцирования v:
Ускорение – это вторая производная по времени от смещения:
Ускорение максимально, если Тогда

колебания
График скорости v(t) тела, совершающего гармонические колебания
График ускорения a(t)

тела, совершающего гармонические колебания

xmax=A0

суммой кинетической и потенциальной энергий:

Подставляя в эту

формулу

выражение для скорости v:

выражение для смещения x:

и, учитывая, что

получаем:



так как: (основное тригонометрическое тождество)




Из формулы: следует, что энергия гармонического колебания:

1) Прямо пропорциональна квадрату амплитуды А2: чем больше “размах” колебаний, тем больше и их энергия.
2) энергия прямо пропорциональна квадрату круговой частоты колебаний ω0.

ВАЖНО!

на нити или пружине и совершающее гармонические колебания.
Пружинный

маятник

Математический маятник

Физический маятник

Пружинный маятник − это материальная точка массой m, подвешенная на абсолютно упругой пружине жесткостью k и совершающая гармонические колебания под действием упругой силы.

Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити длиной l, на которой подвешена материальная точка массой m.

Физический маятник - это твердое тело массой m, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела

где величину I/ml=lпр называют приведенной длиной физического маятника. Она численно равна длине такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

величина изменяется во времени:
с постоянной частотой  по закону

синуса или косинуса и
постоянной амплитудой А0.

Рассмотрим случай действия на тело массой m только силы упругости Fупр

Если пружину оттянуть (на рисунке) или сжать (аналогично, но в другую сторону) на расстояние x от положения равновесия,
то возникает сила упругости Fупр , величина и направление которой определяется законом Гука:



Знак “минус” показывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения x, т.е. к положению равновесия.

На примере движения пружинного маятника – материальной точки массой m, закреплённой на ГОРИЗОНТАЛЬНОЙ пружине жёсткостью k (Рис.1), рассмотрим различные виды колебаний в зависимости от сил, которые действуют вдоль оси Ох на данное тело массой m.

на ось Ох:

Вспомним, что ускорение – это вторая производная

по времени от смещения х:

Получаем уравнение:

Разделим каждое слагаемое на m и вспомним, что ,

где ω0 – собственная круговая частота гармонического колебания.

Получилось дифференциальное уравнение второй степени:
решением которого является:

Тут φ0 не равно 0

Гармонические колебания

График гармонического колебания – синусоида, по которой можно определить смещение х колеблющейся точки в любой момент времени t.

изменяется во времени с постоянной (!) частотой  (круговой

частотой ω) по закону синуса или косинуса, но амплитуда колебания А всё время уменьшается.

В данном случае на тело массой m вдоль оси Ох действуют уже две силы:
сила упругости Fупр
сила трения Fтр .

Сила трения Fтр пропорциональна скорости колебания v и направлена в сторону, противоположную скорости:


Для данного случая второй закон Ньютона в проекции на ось Ох:

и переносе всех членов влево от знака равенства, получим:

Проведем

замену:

где β называется коэффициентом затухания - это основная характеристика затухающего колебания, измеряется в обратных секундах (с-1),

Получаем конечный вид дифференциального уравнения второй степени:



Решением его является формула:

где – собственная круговая частота затухающего колебания.

Затухающие колебания

Мы вывели, что для того случая второй закон Ньютона в проекции на ось Ох:

последовательных амплитуд, разделённых периодом колебания:

Логарифмический декремент затухания λ («лямбда») –
натуральный логарифм декремента затухания:




Логарифмический декремент затухания применяется чаще, т.к. он связан с периодом Т и коэффициентом затухания β:





Обе характеристики – безразмерные величины.

Характеристики затухающего колебания

График затухающего колебания – синусоида, амплитуда которой А(t) уменьшается по экспоненте:

Коэффициент затухания β характеризует степень затухания колебаний.

которое амплитуда уменьшается в e раз:
Характеристики затухающего колебания
Коэффициент затухания

β («бета») – величина, обратная промежутку времени, за который амплитуда колебаний уменьшается в e раз:

Измеряется в СИ в Герцах (Гц) или обратных секундах (с-1)

За время релаксации  система успевает сделать Ne колебаний:

Значит, логарифмический декремент затухания λ обратно пропорционален по величине числу колебаний, за которые амплитуда колебаний уменьшается в е раз:

Добротность Q системы - величина, характеризующая уменьшение полной энергии ΔЕ системы по формуле: ΔЕ = -2πЕ/Q , где знак минус показывает, что энергия уменьшается.
Бóльшим значениям Q соответствует слабое затухание колебаний. Добротность пропорциональна числу колебаний за время релаксации Ne и обратно пропорциональна логарифмическому декременту затухания λ:

оси Ох действуют три силы:
сила упругости Fупр
сила трения

Fтр .
вынуждающая сила Fв, которая действует периодически с круговой частотой ωв:

Для данного случая второй закон Ньютона в проекции на ось Ох:

Учтём, что: и

При сокращении каждого слагаемого на m и переносе всех членов влево от знака равенства, получим:

Вынужденные колебания

Вынужденные колебания – колебания, при которых наблюдаемая величина изменяется во времени:
с постоянной частотой ν (круговой частотой ω), задаваемой внешней вынуждающей силой Fв.

второй степени:


Решение такого уравнения состоит из двух частей-решений: х=х1+х2:
Решение

х1 описывает неустановившейся режим колебаний, когда их амплитуда увеличивается во времени.
Решение х2 описывает установившийся режим колебаний.

В установившемся режиме вынужденных колебаний смещение х2 подчиняется гармоническому закону
и происходит с частотой ωв.

удельная вынуждающая сила

выше параметров:
частоты собственных колебаний 0 ,
коэффициента затухания

,
силы f0 ,
частоты вынуждающей силы в.

Амплитуда А будет максимальна, если частота в действия вынуждающей силы определяется формулой:


При этом наблюдается явление резонанса.

Резонанс – это резкое возрастание амплитуды А вынужденных колебаний при совпадении частоты действия вынуждающей силы в с частотой системы , т.е.:

Если бы затухание в системе отсутствовало ( = 0), то резонанс наступал бы
при условии: 0 = в, где 0 – собственная частота гармонического колебания.
При этом амплитуда достигала бы бесконечно большого значения.

– колебательная система без трения:
при резонансе амплитуда xmax

вынужденных колебаний неограниченно возрастает;
2, 3, 4 – реальные резонансные кривые для колебательных систем с различной добротностью: Q2 > Q3 > Q4.
На низких частотах (ω << ω0) xmax ≈ fmax. На высоких частотах (ω >> ω0) xmax → 0

колебательная система с коэффициентом затухания β

сигналов (Digital Signal Processing – DSP) находят все более

широкое применение, вытесняя постепенно методы, основанные на аналоговой обработке.

Пусть имеется непрерывный сигнал x(t), заданный на интервале [0;∞].

При переходе к оцифровке происходит следующая операция. Выбирается шаг дискретизации T, и вместо исходного сигнала получается последовательность:

В процессе оцифровки аналоговых сигналов имеется два важнейших параметра, определяющих качество цифрового сигнала:
Частота дискретизации
Разрядность оцифровки

Дискретизация предполагает получение мгновенных значений (выборок) аналогового сигнала с определенным временным шагом.

широкий спектр сигнала может быть представлен в дискретном сигнале.

Для того чтобы однозначно восстановить исходный сигнал, частота дискретизации должна более чем в два раза превышать наибольшую частоту в спектре сигнала!

Частота дискретизации (или частота семплирования) – частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в Герцах.

непрерывного сигнала на конечное число интервалов.

Чем больше глубина

дискретизации, тем точнее цифровой сигнал, полученный аналого-цифровым преобразователем (АЦП), соответствует аналоговому.

При оцифровке сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит,
выражающих амплитуду сигнала.

колебаниях
Механические колебания
Составители:
Директор по маркетингу и сбыту, к.т.н. Романов

Р.А.
Руководитель учебного центра «БАЛТЕХ» Севастьянов В.В.

ОСНОВНЫЕ ЗАКОНЫ КЛАССИЧЕСКОЙ МЕХАНИКИ